In the following we will consider the computational efficiency of the traditional and the new implementations of the SOLA method. We remark that for sparse and structured matrices, for which the iterative LSQR algorithm should be used, the flop counts depend on the sparsity and structure of the matrix as well as the necessary number of iterations.
We calculate the number of floating point operations used in the
algorithms as a function of the problem size. The ``size'' of the
problem is characterized by three constants: The number m of
kernels, the number n of points used in the discretization of the
target functions and kernels, and the number q of target functions,
i.e., the number of points where we wish to determine 
. The
relative sizes of m, n and q will depend on the actual
application area, but it is often the case that 
.
Since the reduction to unit covariance form is the only part of the
algorithms that depends on the covariance matrix 
, we have chosen
to analyze this preprocessing step separately, and to analyze the
algorithms under the assumption that we have a problem in unit
covariance form, i.e., the associated covariance matrix is the
identity matrix.
The actual amount of statistical information available may vary a
great deal, depending on the application area. In fact, it is often
very difficult to estimate the covariance matrix. In helioseismology,
for instance, computing the 
's from the solar data is a complex
process where the correlations are not well known. Some experiments
have been performed on artificial data, and they seem to indicate that
the covariance matrix has rather small off-diagonal elements,
suggesting that the data may be described satisfactory by a diagonal
or banded covariance matrix with little bandwidth; see Schou et
al. (1995).
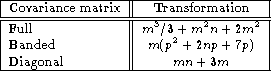
Table 2: Flop counts for transformation to unit covariance form; p is the
bandwidth
In Table 2 (click here) we list the computational cost of
the preprocessing step for a full covariance matrix, a banded
covariance matrix with bandwidth p, and a diagonal covariance matrix,
respectively. For a full 
covariance matrix the time
spent computing the Cholesky factorization is excessively large.
In the more usual case where the variance of the individual errors is
known in advance, but no information about correlations between the
errors is available, the transformation consists in a simple scaling
of the rows in the kernel matrix and a similar scaling of the data and
will not contribute significantly to the overall computation time. We
emphasize that this transformation is done only once, even if
the problem is being solved for several values of 
and/or
target functions.
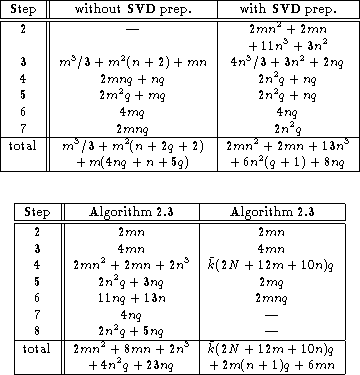
Table 3: Flop counts for
Algorithms 2.3 (click here)-2.3 (click here).
The quantity 
is the average number of
iterations, and N is the number of flops in a
matrix-vector multiplication
Table 4: Flop counts for
Algorithm 2.1 (click here) with and
without SVD preprocessing
In Tables 3 (click here) and 4 (click here) we summarize the detailed flop counts for Algorithms 2.1 (click here)-2.3 (click here).
In connection with the iterative algorithm used in Step 4 of
Algorithm 2.3 (click here), the quantity N denotes the
number of flops involved in a matrix-vector multiplication with 
,
and 
denotes the average number of iterations
(since k will typically depend on 
).
If 
is sparse, then N is twice the number of
nonzeros in the matrix, and if 
has Toeplitz form then
N is proportional to 
.
We shall not comment further on the efficiency of this algorithm, since
the flop counts depend dramatically on N.
If we consider the case where one wants
to calculate 
, 
and the corresponding averaging
kernels at q specified points 
and q
is equal to the number n of discretization points, then the number
of flops used by the three algorithms are as follows:
Obviously Algorithm 2.1 (click here) without the SVD preprocessing
is prohibitively slow except for very small problems. The other two
approaches are comparable, Algorithm 2.3 (click here) being faster if
. A question of special interest is the amount of work
needed to re-compute the solution when 
is changed:
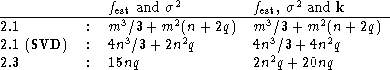
Here Algorithm 2.3 (click here) is clearly superior.
In most
parameter-choice methods, only 
and 
have to be
re-computed - a fact that makes Algorithm 2.3 (click here) even more
attractive.
A crucial factor in mollifier methods is the shape of the chosen
target function 
. Therefore it is likely that solutions
corresponding to a series of differently shaped target functions are
computed. Below we list the number of flops used when q
target functions are changed:
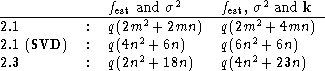
Again, Algorithm 2.3 (click here) is the most efficient - although
the difference is not as dramatic as above.
Pijpers & Thompson (1994) demonstrated that for helioseismic
inversion it is possible to determine an automatic scaling of the
width of the (Gaussian) target functions 
. From
physical arguments it is possible to derive an expression that relates
the smallest length scale by which the rotation can be resolved at
radius 
to certain physical quantities. They demonstrate that
once the optimal target width has been computed at 
, this
relation can be used to scale the target width at any
radius. Using this scaling the optimal value of 
for each
can be computed efficiently using Algorithm 2.3 (click here).