factorization
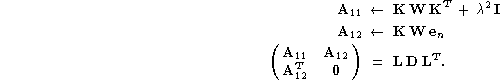
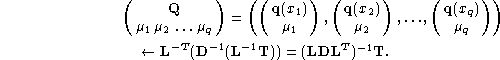
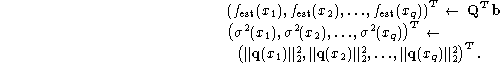
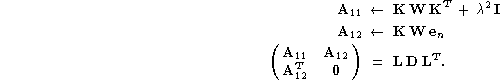
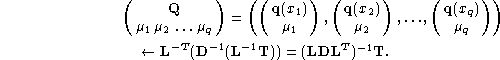
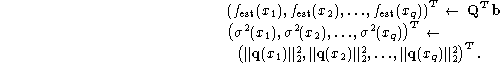
In practice one may wish to repeat the algorithm for different shapes of the
target function 
and/or varying values of the
regularization parameter 
.
Changing the target functions requires re-computing steps
4, 5, 6 and 7. Changing 
requires re-computing steps 3, 5,
6 and 7. In Sect. 4 (click here) we will give a detailed analysis
of the number of operations used by the algorithm.
We can identify Eq. (9 (click here)) as an instance of the
well known equality constrained least squares problem (LSE); see
Lawson & Hanson (1974), Chap. 20. To realize this, let us
introduce the following quantities:
Using this notation we can write (9 (click here)) in the following
form:
These are in fact the normal equations for a constrained least squares
problem, for which we have the equivalent expression:
We can reformulate this as
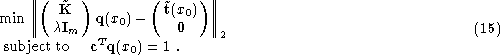
We now have an equality constrained least squares problem in
unit covariance form. Several methods have been developed for solving
problem LSE. Here we use the one described in Lawson & Hanson (1974), Chap. 20
and Golub & Van Loan (1989), Sect. 12.1.4.
The method has three stages:
We can determine a parameterization of the set 
of vectors
in 
that satisfy the constraint in Eq. (15 (click here)):
To do this we compute an 
Householder transformation
(see Golub & Van Loan 1989, Sect. 5.2) such that
In practice 
is not computed explicitly, but is represented in
the form 
. The columns of 
form a basis
for 
and conceptually we can partition 
as
where 
.
It follows that 
can be represented as
where 
is an arbitrary
(m-1)-vector (since all the columns of 
are orthogonal to 
).
We can exploit this fact to transform problem LSE into the
following form, where we have inserted Eq. (16 (click here)) into
Eq. (15 (click here)) and collected terms:
We now multiply from the left under the norm-sign with the orthogonal matrix
without changing the solution. Using the orthogonality of 
we
finally arrive at the reduced problem
This is an ordinary unconstrained least squares problem. Having solved
this for 
we obtain the solution to the original constrained
problem as
We now describe an algorithm for solving (17 (click here)) which
is efficient when many values of 
are required.
Following Eldén (1977) we first bring
into bidiagonal form:
where
Here 
, 
, and 
is lower
bidiagonal. This is the most costly part of the computation, it
requires 
flops. The remaining part of the algorithm
only involves 
, which means that the dimension of the problem is
effectively reduced from 
to 
. As in the SVD
transformation, 
is not explicitly computed, but 
is computed ``on the fly''. If 
is required for
computing the discretized kernel 
, then the orthogonal
transformations that 
consists of are stored for later use. For
algorithmic details on bidiagonalization see, e.g.,
Golub & Van Loan (1989), pp. 236-238.
If we make the transformation of variables
then we easily see that (17 (click here)) is equivalent to
This least squares problem is now solved by determining a series of
2n-1 Givens rotations 
(see Golub & Van
Loan 1989,
Sect. 5.2) such that
where 
is 
lower bidiagonal. The part of the
right-hand side denoted by ``
" consist of n non-zero elements
introduced along the way, but these are not computed in practice. We
illustrate this procedure on a small example with n=3. First a
rotation 
applied to rows n and 2n annihilates the (2n,n)-element,
and a nonzero element is created in position (2n,n-1); then we annihilate
this element by a rotation 
applied to rows 2n-1 and 2n:
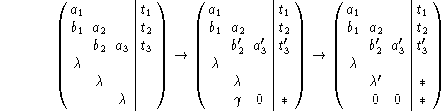
where
In the next step the same procedure is applied to the leading 
sub-matrix to annihilate the element in position
(2n-1,n-1), and so on. During the reduction we only need
to store the diagonals of 
in a pair of vectors, and the current
value of 
.
Now the solution 
can be computed as
For a large sparse or structured (e.g., Hankel or Toeplitz) matrix
it is prohibitive to compute explicitly the full
bidiagonalization in Eq. (19 (click here)). Instead we would
prefer to keep 
in factored form
and use an iterative algorithm to solve the system
in (17 (click here)). An efficient and stable algorithm for doing
this, based on Lanczos bidiagonalization (Golub & Van
Loan 1989, Sect. 9.3.3), is the algorithm
LSQR, Paige & Saunders (1982a).
This algorithm only accesses the coefficient matrix 
via
matrix-vector multiplications with 
and 
.
An even more efficient approach is to apply the LSQR algorithm
with 
and use the fact that the kth iterate 
is a regularized solution. To be more specific, when we apply
LSQR to Eq. (17 (click here)) with 
, i.e.,
to 
then the iteration number k plays the role of the
regularization parameter; small k correspond to large 
, and
vice versa. The reason is that LSQR captures the spectral
components of the solution in order of increasing frequency, hence the
initial iterates are smoother than the iterations in later stages, and
as a consequence the initial iterates are more regularized.
The LSQR algorithm with 
is equivalent to Lanczos
bidiagonalization of 
.
Specifically, after k steps, the Lanczos bidiagonalization algorithm
has produced three matrices 
,
, and 
such that
where both 
and 
have orthonormal columns,
and 
is bidiagonal.
Moreover, the first k columns of 
, the first k-1 columns
of 
, and the leading 
sub-matrix of 
are identical to the corresponding quantities in the previous step of
the algorithm.
The kth iterate 
is then computed as
where 
solves the problem
The key to the efficiency of LSQR lies in the way that 
is
updated to 
, while 
and 
are
never stored; we refer to Paige & Saunders (1982a) for more details.
We emphasize the difference between the two bidiagonalization procedures.
The full bidiagonalization (19 (click here)) is explicitly computed once, and
it is independent of the regularization parameter; 
enters
when solving the augmented bidiagonal system in Eq. (22 (click here)).
The Lanczos bidiagonalization appears implicitly in computing the
LSQR iterates 
, and the sequence of iterates
corresponds to sweeping through
a range of regularization parameters.
To compute the solution to the original problem in (15 (click here)) it is
necessary to transform the solution 
or 
to the original variable 
.
Below 
and 
denote either
and 
from Sect. 2.2.2 (click here) or
and 
from Sect. 2.2.3 (click here).
Inserting Eq. (18 (click here)) and
(21 (click here)) in Eq. (2 (click here)) we get
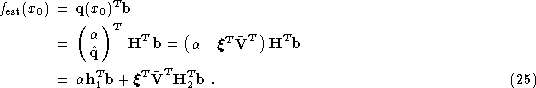
Similarly, if we insert Eqs. (18 (click here)),
(19 (click here)) and (21 (click here)) in Eq.
(10 (click here)) and use the definition of 
then we get
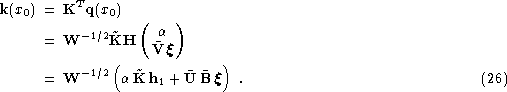
Finally, due to the orthogonality of 
and 
the variance of the error in 
due to the noise takes the form
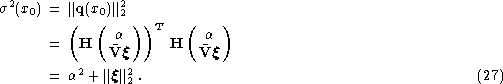
Consider first full bidiagonalization from Sect. 2.2.2 (click here).
We notice that 
is the only quantity in the
above expressions that depends on the regularization parameter 
and the target function 
.
Therefore 
and 
only need to be
computed once (in fact, they are already computed in earlier stages of
the algorithm).
This means that re-computing the solution 
when changing 
or
is very cheap.
This is a great improvement
compared with the Lagrange-multiplier method from Sect. 2.1 (click here),
where a matrix factorization must re-computed each time.
Although we do not explicitly compute 
, it is still quite
inexpensive to compute the discretized averaging kernels 
for the different solutions.
Again, one of the terms, namely 
, is already computed
in earlier steps of the algorithm and the term 
requires only approximately 
flops.
Consider next the case from Sect. 2.2.3 (click here) where we use
Lanczos bidiagonalization. Again, only 
depends on
the target function 
, but now both 
and 
depend on the regularization parameter, i.e., the iteration number k.
Moreover, they both appear only implicitly in the algorithm, while it
is the iteration vector 
that is explicitly computed.
It is now more efficient to use the formulation
to compute
the estimated solution, and the variance of the error in 
is given by
.
Similarly, the discretized averaging kernel should be computed by
means of 
.
Our new algorithms, based on bidiagonalization, are summarized
below. They describe the general case where 
is computed at
points 
. The matrix 
below is again the matrix
whose columns contain ``samples'' of the q target function:
, 
,
.