algorithm: SOLA by elimination of theconstraint (full bidiagonalization)

1. Transform to standard form
   
   
2. Set up LSE problem
   
   
3. Generate Householder transformation and apply it to to get the reduced problem
   
   
4. Compute the bidiagonalization of and change variables.
   
   
5. Modify the right-hand sides.
   
   
6. Apply Givens rotations to get lower bidiagonal and solve for
   
   
7. Compute the estimates of f and the corresponding variances at
   
   
8. If needed, compute the corresponding averaging kernels
   
   

 

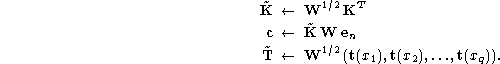
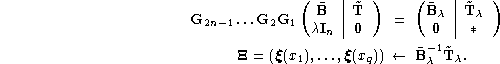
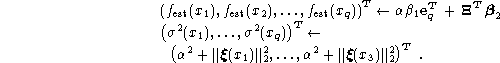
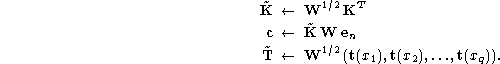
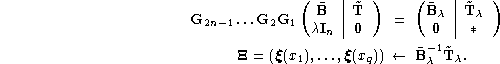
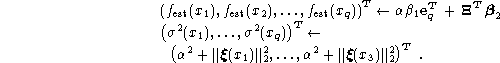
Here step 4 completely dominates the computation time. Changing the target functions requires re-computing the last part of step 2 plus steps 5 through 8. Changing requires re-computing steps 6 through 8. In Sect. 4 (click here) we will give a detailed analysis of the number of operations used by the algorithm.