Having presented the algorithm we will briefly discuss how they can be implemented in practice. Any specific implementation will depend on the architecture of the specific platform used. A common approach is to use the Basic Linear Algebra Subroutines (BLAS). The BLAS has become a de facto standard and FORTRAN BLAS routines are supplied by most computer vendors in highly optimized version for their specific machine(s). Most vendors also supply a C interface to the BLAS. Among the BLAS subroutines we find most of the necessary building blocks for the algorithms presented: Solution of triangular systems of equations, Givens rotations, Householder transformations (rank-1 update), etc.
The more complex ``building blocks'' such as the Cholesky
factorization, the Bunch-Kaufmann 
factorization,
the SVD, and the bidiagonalization are not part of the BLAS. These
routines are available in most mathematical software libraries, such
as LINPACK, Dongarra et al. (1979), LAPACK, Anderson et
al. (1992), NAG (1991), and
IMSL (1991), and some are also found in Numerical Recipes,
Press et al. (1992). In Table 1 (click here) we have
listed the relevant subroutines in the different libraries. Only
LAPACK and NAG contain bidiagonalization routines, in the other
libraries this operation is a part of the SVD routine.
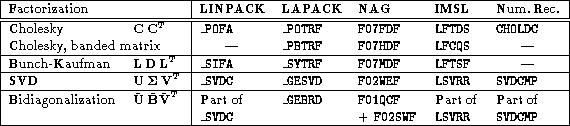
Table 1: Subroutines to be used as ``building blocks'' for the algorithms
In the sparse/structured case, the core of the computations lies in the LSQR algorithm which is available in FORTRAN; see Paige & Saunders (1982b).