To illustrate our bidiagonalization methods we have included a
numerical example from inverse helioseismology.
The problem consists in inferring the solar rotation rate as a function
of radius from the rotational frequency-splittings of the
eigen-oscillations observed on the solar surface. We use a subset of
mode set 1 from Christensen-Dalsgaard et al. (1990), restricted
to the frequency range 2.75-3.25 mHz. This reduced set contains
212 modes of degrees
see Christensen-Dalsgaard et al. (1990) and references therein
for further details on the rotational inversion problem. This example
is identical to the 1-D test problem used by Hanke &\
Hansen (1993) and the dimensions of the kernel-matrix are m =
212 and n = 100. As target functions we use a Gaussian of width
:
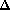where 
is a normalization factor and x is the
fraction of solar radius 
.
The errors in the right-hand side are Gaussian with zero mean,
standard deviation 
, and uncorrelated.
All our calculations are carried out in MATLAB on an HP9000/819
workstation with machine precision 
and IEEE
arithmetic. For simplicity we use the midpoint quadrature rule to
calculate the weights in 
.
Figure 1 (click here) shows the
target function and the computed averaging kernels 
for
and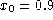 
, computed by means of both full
bidiagonalization and Lanczos bidiagonalization. The averaging kernels computed by Algorithm 2.3 (click here) (the
Lanczos-based algorithm) with k=35 are almost identical to those
computed by Algorithm 2.3 (click here) with 
.
Figure 2 (click here) shows the ``trade-off plots'' of the
Algorithms 2.3 (click here) and 2.3 (click here) at the two points
and 
.
Define the error magnification as the ratio of the standard deviation of the
error in 
due to the noise, 
,
to the standard deviation 
of the errors.
We plot the error magnification versus the
residual norm 
for varying values of the regularization parameters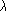 
and k.
The solid line shows the trade-off curve for
Algorithm 2.3 (click here) using full bidiagonalization with
ranging from 
(top left) to 1.4 (bottom
right). The ``optimal'' value of 
, corresponding to the
corner of the trade-off curve, is approximately 
.
The dots represent the discrete trade-off curve associated with
Algorithm 2.3 (click here), using Lanczos bidiagonalization. The
regularizing effect of the Lanczos-based algorithm is clearly seen: As
the iterates are generated the algorithm effectively sweeps through a
range of regularization parameters, reaching the optimal solution
after approximately 35 iterations.
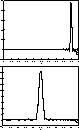
Figure 1: Top: Computed averaging kernels
for the estimate at 
. The target
width 
is 
. The dashed and the dotted lines are the
averaging kernels for the almost identical solutions computed by
means of full bidiagonalization with 
and Lanczos bidiagonalization with k=35, respectively. The
solid line is the target function 
.
Bottom: The same plot
for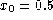 
, 
, 
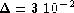and k=35
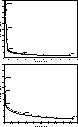
Figure 2:
Top: Trade-off curves of the error magnification 
versus the residual norm 
, at 
with 
. The solid line is the trade-off
curve for the solutions computed by means of the full
bidiagonalization procedure values of 
in the
interval from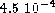 
to 1.4. The dots represent the
discrete trade-off curve of the Lanczos-based method. The
solutions corresponding to 5, 10, 35, 80 and 100 iterations
are marked on the plot. Bottom: The same plot for 
and 