Having calculated the (flux weighted) line-strength distribution and
appropriate force-multipliers as function of local variables, one could
argue that the problem is solved, since, after performing the required
regressions with respect to
![]() and
and
![]() (see Kudritzki et
al. [1998]), these values can be tabulated and the hydro-equations
solved. In the following, we want to proceed a step further and try to
understand the basic physics which determines the slope of the distribution
in some detail. Note again that the actual value of this quantity is
decisive for all astrophysical problems involving radiatively driven
mass-loss (cf. Sect. 1), and that only a thorough understanding of the
individual processes which determine this quantity enables us to draw
correct conclusions and to give quantitatively correct predictions.
Moreover and although it is empirically known that
(see Kudritzki et
al. [1998]), these values can be tabulated and the hydro-equations
solved. In the following, we want to proceed a step further and try to
understand the basic physics which determines the slope of the distribution
in some detail. Note again that the actual value of this quantity is
decisive for all astrophysical problems involving radiatively driven
mass-loss (cf. Sect. 1), and that only a thorough understanding of the
individual processes which determine this quantity enables us to draw
correct conclusions and to give quantitatively correct predictions.
Moreover and although it is empirically known that ![]() is of order
0.4 ...0.6 in most situations (leading to the aforementioned similarity
of
is of order
0.4 ...0.6 in most situations (leading to the aforementioned similarity
of ![]() and
and
![]() ), there is no a priori reason that the steepness
of the line-strength distribution function lies in this range, and,
especially, that
), there is no a priori reason that the steepness
of the line-strength distribution function lies in this range, and,
especially, that
![]() over a large range of line-strengths.
over a large range of line-strengths.
From the definition of the flux-weighted line-strength distribution, there are three essential quantities to be considered in order to predict its behaviour, namely the oscillator strength distribution of contributing lines, the level population of the absorbing/re-emitting levels and the irradiating flux. In a first and more tutorial step, we consider the most simple case being possible, namely the case of pure hydrogen (or, more generally, hydrogenic ions), which states the complete problem (including the influence of NLTE-effects) in an analytically understandable way and leads to a number of interesting results.
The gf-value of a given transition between principal quantum number n'and n (summed over all contributing angular momenta, i.e. accounting for selection rules) is given by the well known Kramers formula (neglecting Gaunt-factors of order unity)
At first, consider only resonance transitions n' = 1, in which case
![]() with C the numerical constant in (44).
The number of possible transitions up to a certain principal quantum number
n is
with C the numerical constant in (44).
The number of possible transitions up to a certain principal quantum number
n is
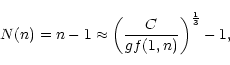 |
(45) |
so that the (cumulative) number of transitions with gf-values stronger/equal than a certain value gf reads
Thus, the resulting distribution function
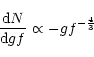 |
(47) |
is given by a power-law, where the exponent corresponds to an ![]() -value
of 2/3, i.e., is just the canonical value which would lead to a
mass-independent WLR and is consistent with the observations of
O-Supergiants (cf. Puls et al. [1996]).
-value
of 2/3, i.e., is just the canonical value which would lead to a
mass-independent WLR and is consistent with the observations of
O-Supergiants (cf. Puls et al. [1996]).
Thus, from the above arguments one might conclude that the major problem is
solved, and that the calculated/observed
![]() values are
dominated by the oscillator-strength statistics. Note already here, however,
that the majority of driving lines (non-hydrogenic!) cannot be described
similarily, since the dominant ingredient in the above derivation - the
rather simple and specific dependency of atomic quantities (oscillator
strength and energy levels) on principal quantum number - is no longer
valid in more complex ions.
values are
dominated by the oscillator-strength statistics. Note already here, however,
that the majority of driving lines (non-hydrogenic!) cannot be described
similarily, since the dominant ingredient in the above derivation - the
rather simple and specific dependency of atomic quantities (oscillator
strength and energy levels) on principal quantum number - is no longer
valid in more complex ions.
Two additional points are worth mentioning. First, by using the "exact''
Kramers law accounting for the
(1 - n-2) term, the apparent slope at
large gf-values becomes steeper than -4/3, leading to
![]() ,
which again is consistent with the behaviour of "realistic'' line-strength
distribution function.
,
which again is consistent with the behaviour of "realistic'' line-strength
distribution function.
Second, by accounting also for transitions between excited levels, one finds (see below) the same statistics, i.e., the exponent -4/3 (with lower values for large gf) is universal for hydrogen-like ions.
| |
Figure 5:
gf-distribution for hydrogen, calculated by Kramers-formula
(Eq. 44) for |
Figure 5 displays the cumulative gf-distribution function for
principal quantum numbers ![]() (with sufficiently large
(with sufficiently large ![]() ),
both for the individual series (n' fixed) denoted by crosses as well as
for all combinations of n',n (fully drawn). Following a steep increase
from the maximum value, the distribution displays a rather constant slope
(in the log) of -1/3 (cf. Eq. 46) over four dex, before it
reaches its final, constant value resulting from running out of lines
(depending on the maximum value chosen for n). This behaviour compares
well to our case "A'' discussed in Appendix A.
Concerning the
individual series, the higher ones follow exactly the predicted slope from
the approximation given below (49), whereas the high gf-tails
of the lower series have a somewhat steeper slope, as discussed above. Note
also, that the gf-values from the higher series are generally larger than
those from the lower ones.
),
both for the individual series (n' fixed) denoted by crosses as well as
for all combinations of n',n (fully drawn). Following a steep increase
from the maximum value, the distribution displays a rather constant slope
(in the log) of -1/3 (cf. Eq. 46) over four dex, before it
reaches its final, constant value resulting from running out of lines
(depending on the maximum value chosen for n). This behaviour compares
well to our case "A'' discussed in Appendix A.
Concerning the
individual series, the higher ones follow exactly the predicted slope from
the approximation given below (49), whereas the high gf-tails
of the lower series have a somewhat steeper slope, as discussed above. Note
also, that the gf-values from the higher series are generally larger than
those from the lower ones.
A simple expansion of Eq. (44) clarifies the behaviour of the gfdistribution for not too large gf-values: To first order, the upper level n for given gf-value and lower level n' results to
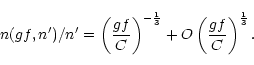 |
(48) |
Thus, the total number of lines with gf-values larger than a certain one is given by
where C is the numerical constant in Eq. (44) and
![]() the
maximum lower level of the considered transitions, which controls the
vertical offset of the distribution function. Note, that the last equation
(all transitions) compares exactly to Eq. (46) (only
resonance lines), except from the generalization to
the
maximum lower level of the considered transitions, which controls the
vertical offset of the distribution function. Note, that the last equation
(all transitions) compares exactly to Eq. (46) (only
resonance lines), except from the generalization to
![]() .
.
| |
Figure 6:
Cumulative line-strength distribution function
for hydrogen (see Eq. 50). "Atomic model'' as in
Fig. 5, gf-values from Kramers-formula and excitation in
LTE. Triangles: analytic approximation for small |
(For the definition of
![]() with n1 the ground-state
occupation number and
with n1 the ground-state
occupation number and
![]() ,
see Eq. D5.)
Obviously, also the line-strength distribution follows the
"canonical'' power-law
,
see Eq. D5.)
Obviously, also the line-strength distribution follows the
"canonical'' power-law
![]() ,
which is, of
course, the final consequence of the primary dependence of
,
which is, of
course, the final consequence of the primary dependence of
![]() for each series. Excitation plays only a minor role,
controlling the function
for each series. Excitation plays only a minor role,
controlling the function
![]() and thus the vertical offset (or, in
other words, the normalization constant): the higher the temperature, the
more lines are present if the ionization structure would remain constant,
i.e., if
and thus the vertical offset (or, in
other words, the normalization constant): the higher the temperature, the
more lines are present if the ionization structure would remain constant,
i.e., if ![]() would not change. Again, we have compared the analytical
prediction with the numerical simulation (Fig. 6), which gives a
perfect agreement in the valid range and even beyond! Note also, that the
asymptotic behaviour
would not change. Again, we have compared the analytical
prediction with the numerical simulation (Fig. 6), which gives a
perfect agreement in the valid range and even beyond! Note also, that the
asymptotic behaviour
![]() is consistent with our
requirement that
is consistent with our
requirement that
![]() for
for
![]() ,
which
has to be fulfilled in order to validate Eq. (21).
,
which
has to be fulfilled in order to validate Eq. (21).
Fortunately, the flux irradiating these strong IR-transitions is small, and
the primary contribution to the line-force is only due to transitions
near the flux maximum, a fact which is exploited a priori in our simplified
NLTE-calculations (cf. Sect. 3.1.2 and Abbott & Lucy [1985]). With
respect to the hydrogen atom under consideration, we expect therefore the
Lyman series (including the Balmer series for A-stars) to be the major
contributor for radiative momentum. To this end, the long-dashed curve in
Fig. 6 displays the line-strength distribution for the
Lyman-Series only (
![]() K), together with the analytical
approximation (asterisks), whereas the fully drawn one corresponds to the
final, flux (times frequency) weighted distribution accounting for all
considered lines: Obviously, our expectation is met precisely. Note,
however, that Fig. 6 serves only as a tutorial and overestimates
the real situation by far, since due to line convergence near the ionization
edge only a few lines (
K), together with the analytical
approximation (asterisks), whereas the fully drawn one corresponds to the
final, flux (times frequency) weighted distribution accounting for all
considered lines: Obviously, our expectation is met precisely. Note,
however, that Fig. 6 serves only as a tutorial and overestimates
the real situation by far, since due to line convergence near the ionization
edge only a few lines (
![]() )
can be treated as individual ones, thus
cutting the distribution function at this value.
)
can be treated as individual ones, thus
cutting the distribution function at this value.
So far, we were concerned only with the slope of the line-strength
distribution and its relation to the line-force parameter
![]() .
Almost nothing has been said on the normalization constant
.
Almost nothing has been said on the normalization constant ![]() (Eq. 10), which controls the absolute value of the acceleration due
to its relation to the total line number. We have pointed out that
(Eq. 10), which controls the absolute value of the acceleration due
to its relation to the total line number. We have pointed out that ![]() may
have an additional depth dependence, which transforms, via
Eq. (16), into a depth dependent line-force parameter
may
have an additional depth dependence, which transforms, via
Eq. (16), into a depth dependent line-force parameter
![]() .
This
additional depth dependence originates, of course, from the behaviour of the
mass absorption coefficient
.
This
additional depth dependence originates, of course, from the behaviour of the
mass absorption coefficient
![]() present in the definition of
the line-strength
present in the definition of
the line-strength ![]() .
Although this ratio remains more or less constant
if we consider the primary source of radiative driving, namely resonance
lines and lines with a lower meta-stable level from main ionization
stages (denoted in the following by "j''), there will be always a
"contamination'' by lines from excited levels and, most important, by lines
from minor ionization stages.
.
Although this ratio remains more or less constant
if we consider the primary source of radiative driving, namely resonance
lines and lines with a lower meta-stable level from main ionization
stages (denoted in the following by "j''), there will be always a
"contamination'' by lines from excited levels and, most important, by lines
from minor ionization stages.
Since H I is such a trace ion in hot star winds, we will investigate
the effects of this depth dependence in our tutorial chapter. It is well
known (e.g. Mihalas [1978], p. 125) that the NLTE ground state
departure coefficient of a trace ion one stage below the major one in a
spherical atmosphere is primarily a function of the inverse of the dilution
factor
![\begin{displaymath}W(r) = {1 \over 2}\bigl[1-\bigl(1-(R_{\ast}/r)^2\bigr)^{1 \over 2}\bigr].
\end{displaymath}](/articles/aas/full/2000/01/ds8655/img340.gif)
Since nj varies in concert with the local density, the ratio
![]() becomes a function of
becomes a function of
![]() ,
which finally leads - besides an additional
temperature dependence - to a variation of
,
which finally leads - besides an additional
temperature dependence - to a variation of ![]() as (cf. Eq. 50)
as (cf. Eq. 50)
In a mixture of major and minor ionization stages, as present in a stellar
wind, we have, of course, a different dependence. However, the notion that
also in this case the ionization structure is primarily controlled by the
factor
![]() (with exponents different from unity if one includes trace
ions of stages j+1, j-2 etc.) lead Abbott ([1982]) to the
introduction of the famous
(with exponents different from unity if one includes trace
ions of stages j+1, j-2 etc.) lead Abbott ([1982]) to the
introduction of the famous ![]() -term to the force-multiplier, which in
terms of our line-strength distribution function reads
-term to the force-multiplier, which in
terms of our line-strength distribution function reads
with
![]() the electron density in units of
the electron density in units of
![]() and
and
![]() now independent of depth. Equation (52) shows that for
hydrogen
now independent of depth. Equation (52) shows that for
hydrogen![]()
![]() should be of order 1/3.
More generally and using the fact that the appropriately scaled variable for
all considerations is
should be of order 1/3.
More generally and using the fact that the appropriately scaled variable for
all considerations is
![]() (Eq. D2), a plasma dominated by trace-ions of stage
j-1 must have a
(Eq. D2), a plasma dominated by trace-ions of stage
j-1 must have a ![]() -value which is just the negative of the
line-strength exponent in the
-value which is just the negative of the
line-strength exponent in the
![]() -distribution, i.e,
-distribution, i.e,
![]() or
or
Figure 7 verifies this equation for a number of different
conditions. We have calculated the force-multiplier arising from hydrogen in
a hot stellar wind plasma under different conditions (see caption), and
obtained the effective values
![]() by first order
derivatives. Although
by first order
derivatives. Although
![]() varies from 0 ...1, the equality
(54) is almost perfectly reproduced. On a first glance, it is
somewhat puzzling that
varies from 0 ...1, the equality
(54) is almost perfectly reproduced. On a first glance, it is
somewhat puzzling that
![]() is so much varying although the according
line-strength distribution has an almost constant slope. In the situation
described here (trace ion of stage (j-1)), however, we have a strong
dependence on local conditions,
is so much varying although the according
line-strength distribution has an almost constant slope. In the situation
described here (trace ion of stage (j-1)), however, we have a strong
dependence on local conditions,
![]() ,
contrasted to the usual case of
,
contrasted to the usual case of
![]() const throughout the wind for the (resonance) lines of major ion species.
Thus, there is only a small strip in the
const throughout the wind for the (resonance) lines of major ion species.
Thus, there is only a small strip in the
![]() plane where we do not
encounter the case of all lines being either optically thick
(
plane where we do not
encounter the case of all lines being either optically thick
(
![]() )
or optically thin (
)
or optically thin (
![]() ). Even in
those cases, however, Eq. (54) is still valid!
). Even in
those cases, however, Eq. (54) is still valid!
Finally,
![]() and
and
![]() holds generally (i.e., for any
type of ionization/excitation) in the optically thick case, since then the
dependence of line-force on occupation numbers vanishes completely and
only the relation
holds generally (i.e., for any
type of ionization/excitation) in the optically thick case, since then the
dependence of line-force on occupation numbers vanishes completely and
only the relation
![]() survives.
survives.
We want to finish this section with two summarizing comments: First, we have
shown that for hydrogen (generally: hydrogenic ions) the gf- distribution
![]() (for each series) leads quite naturally to a
line-strength distribution function with a slope corresponding to
(for each series) leads quite naturally to a
line-strength distribution function with a slope corresponding to
![]() .
Second, the dependence of the line-strength on the specific
type of ionization (major one or trace ion) gives rise to a depth dependent
normalization constant
.
Second, the dependence of the line-strength on the specific
type of ionization (major one or trace ion) gives rise to a depth dependent
normalization constant ![]() ,
finally leading to the
,
finally leading to the ![]() term in the
force-multiplier and line-strength statistics. Since
term in the
force-multiplier and line-strength statistics. Since ![]() is of order
1/3 for trace ions of stage j-1 (which are usually the dominating species
of minor ions, cf. Sect. 4.2.5) and
is of order
1/3 for trace ions of stage j-1 (which are usually the dominating species
of minor ions, cf. Sect. 4.2.5) and
![]() for major ions, the
effective value of
for major ions, the
effective value of ![]() resulting from an appropriate mixture should be
a small, positive number
resulting from an appropriate mixture should be
a small, positive number![]() .
.
Since the predominant radiative acceleration in hot star winds is certainly due to non-hydrogenic ions (e.g., from iron-group elements), we turn now to the line-strength statistics of these elements.
To our knowledge, there are only two previous investigations related to this
topic. On the one hand, Learner ([1982]) found a line-strength
distribution with a typical power-law index corresponding to
![]() by means of experimental data (mostly ionization stages I and
II), a result recently used by Wehrse et al. ([1998]) in their
stochastic approach of line transfer in moving atmospheres. The first step,
however, was taken by Allen ([1966], [1974]) who performed a
thorough analysis of line distributions of neutral elements, aimed at the
goal of establishing a "statistical spectroscopy''. His approach provides a
significant understanding of the resulting statistical description
especially under LTE conditions. The basic philosophy,
however, has turned out to be extremely useful also regarding the problem
under our consideration, at least if some additional considerations are
taken into account. Before we comment on these, we will firstly introduce
the basic concept and convince ourselves that it is applicable for our
purposes. Note that the following results, which allow to understand the
line-strength statistics of individual ions in an almost completely
analytical way (as a function of level density, oscillator-strength
distribution, ionization potential, temperature etc.), will turn out to be
useful also for future investigations related to line-blanketing/blocking
calculations. Finally, by a comparison between actual data and analytic
simulations based on our results, the degree of completeness of present
atomic data bases can be easily checked.
by means of experimental data (mostly ionization stages I and
II), a result recently used by Wehrse et al. ([1998]) in their
stochastic approach of line transfer in moving atmospheres. The first step,
however, was taken by Allen ([1966], [1974]) who performed a
thorough analysis of line distributions of neutral elements, aimed at the
goal of establishing a "statistical spectroscopy''. His approach provides a
significant understanding of the resulting statistical description
especially under LTE conditions. The basic philosophy,
however, has turned out to be extremely useful also regarding the problem
under our consideration, at least if some additional considerations are
taken into account. Before we comment on these, we will firstly introduce
the basic concept and convince ourselves that it is applicable for our
purposes. Note that the following results, which allow to understand the
line-strength statistics of individual ions in an almost completely
analytical way (as a function of level density, oscillator-strength
distribution, ionization potential, temperature etc.), will turn out to be
useful also for future investigations related to line-blanketing/blocking
calculations. Finally, by a comparison between actual data and analytic
simulations based on our results, the degree of completeness of present
atomic data bases can be easily checked.
Following Allen ([1966], [1974]) and neglecting
subtleties, the first important assumption concerns the number of energy
levels in the energy range
![]() ,
which will be described by the
distribution
,
which will be described by the
distribution
![]() .
Although there are certain irregularities, the
basic trend of p(x) is to increase with excitation energy, and Allen
adopted - per ion - a power-law
.
Although there are certain irregularities, the
basic trend of p(x) is to increase with excitation energy, and Allen
adopted - per ion - a power-law
| (55) |
in the range
![]() with (effective) ionization energy
with (effective) ionization energy ![]() .
Note
that this parameterization can be validated for rather complex ions (see the
tests performed below), is however much less appropriate for hydrogenic ions
due to their specific dependence of energy on level number (cf. the examples
given by Allen [1966], Fig. 3). Thus, the approach presented
here and the one given in the previous section are almost mutual exclusive.
.
Note
that this parameterization can be validated for rather complex ions (see the
tests performed below), is however much less appropriate for hydrogenic ions
due to their specific dependence of energy on level number (cf. the examples
given by Allen [1966], Fig. 3). Thus, the approach presented
here and the one given in the previous section are almost mutual exclusive.
With the above distribution, the number of lines between energies x1 and
x2 and per excitation ranges
![]() and
and
![]() is
is
| (56) |
where ![]() shall be the "selection'' factor accounting for selection
rules (typically of order 0.2...0.3 for iron group elements). Since the
transition frequency is given by
shall be the "selection'' factor accounting for selection
rules (typically of order 0.2...0.3 for iron group elements). Since the
transition frequency is given by
![]() ,
when we calculate in
appropriate units (say, kiloKayser = "kK''), the number of lines with
lower levels between
,
when we calculate in
appropriate units (say, kiloKayser = "kK''), the number of lines with
lower levels between
![]() and transition frequencies
and transition frequencies
![]() is
is
In his further derivation, Allen assumed the logarithm of the gf-values
(
![]() )
to be equally distributed within the range
)
to be equally distributed within the range
![]() ,
with
,
with
![]() of order 3 dex. This assumption, being
equivalent to a gf-distribution
of order 3 dex. This assumption, being
equivalent to a gf-distribution
![]() ,
will be
relaxed in the following. Instead, we consider a distribution with
arbitrary, however constant exponent
,
will be
relaxed in the following. Instead, we consider a distribution with
arbitrary, however constant exponent ![]() ,
again independent of
frequency (and excitation energy), so that the number of lines with
,
again independent of
frequency (and excitation energy), so that the number of lines with
![]() -values within
-values within
![]() is given by
is given by
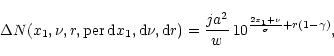 |
(58) |
| w | = | 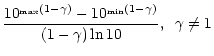 |
|
| w | = | (59) |
Now we define the line intensity by
if we measure energies and frequencies in kK and the temperature in units of 625 K, t = T/625 K (not to be confused with the optical depth parameter defined by CAK).
Note that by introducing the line intensity in this way, one implicitly
assumes that the plasma is in LTE and that all levels connected by
lines play an equally important role, if one uses this quantity as the
primary statistical variable. Note also that under LTE conditions l is
closely related to the negative logarithmic line-strength if the
wavelength dependence of ![]() is ignored.
is ignored.
If we convert the x1-dependence of ![]() into an l-dependence and
integrate over
into an l-dependence and
integrate over ![]() ,
we find the number of lines for given line intensity
and transition frequency as
,
we find the number of lines for given line intensity
and transition frequency as
(Here and in the following, we always assume ![]() .
The case A = 0
can be treated by a somewhat different expansion). In case of
.
The case A = 0
can be treated by a somewhat different expansion). In case of ![]() ,
the second term in the difference can be neglected with respect to the
first one, and we recover the result given by Allen,
,
the second term in the difference can be neglected with respect to the
first one, and we recover the result given by Allen,
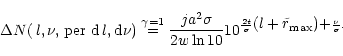 |
(63) |
The difference between
![]() and
and
![]() is the following. Whereas
is the following. Whereas
![]() relates to the maximum
relates to the maximum
![]() -value for the considered ion,
-value for the considered ion,
![]() is the maximum value which is possible for given
is the maximum value which is possible for given ![]() and
and
![]() and underlies the following restrictions:
and underlies the following restrictions:
The interpretation of these expressions is straightforward. If the r-values
are equally distributed between
![]() and
and
![]() ,
the log of
,
the log of ![]() should
increase linearly between
should
increase linearly between
![]() ,
where the slope is controlled
both by the slope of the level density and the temperature. For
all line intensities larger than
,
where the slope is controlled
both by the slope of the level density and the temperature. For
all line intensities larger than ![]() ,
the number of lines should become
constant, until
,
the number of lines should become
constant, until
![]() and the number of
lines approaches zero for
and the number of
lines approaches zero for
![]() .
.
In order to check this and the following predictions, we have calculated the
line intensity statistics for Fe II (comprising roughly 200000 lines)
from our present data base (Sect. 3.1). Instead of using the actual
gf-values, however, we firstly simulated different distributions by a
Monte-Carlo process, with random variable
![]() ,
,

|
Figure 8:
|

|
Figure 9:
As Fig. 8, for T= 10000 K and
|
and replaced the actual gf-value by the value drawn from the above
distribution, with
![]() and
and
![]() .
Thus,
by this simulation we primarily investigate in how far the assumptions
leading to Eq. (57) are justified and inspect the validity of the
overall approach, under the restriction of gf-distributions with constant
slope.
.
Thus,
by this simulation we primarily investigate in how far the assumptions
leading to Eq. (57) are justified and inspect the validity of the
overall approach, under the restriction of gf-distributions with constant
slope.
In the following plots, we display the result for the frequency with the
highest line-density, namely
![]() kK corresponding to
kK corresponding to
![]() Å, and the vertical line gives the transition
line intensity
Å, and the vertical line gives the transition
line intensity ![]() ,
with
,
with
![]() kK.
kK.
The first series (Fig. 8) has been calculated for the case
discussed above, namely
![]() ,
and three different temperatures
,
and three different temperatures
![]() ,
10000, 15000 K. As predicted, the constant, temperature dependent
slope and the kink at
,
10000, 15000 K. As predicted, the constant, temperature dependent
slope and the kink at ![]() are present, as well as the constant line number
for
are present, as well as the constant line number
for
![]() ,
until the maximum possible l (as function of t, see
above) is reached and
,
until the maximum possible l (as function of t, see
above) is reached and
![]() .
.
Next, we consider the case of
![]() .
Here, we have to perform
the following distinction. Let us first assume that
.
Here, we have to perform
the following distinction. Let us first assume that
![]() is not
significantly smaller than
is not
significantly smaller than ![]() ,
i.e.,
,
i.e.,
![]() in the case
of Fe II. Then, we can neglect again the 2nd term in
the difference in Eq. (61) with respect to the first one, and obtain,
accounting for the restrictions concerning
in the case
of Fe II. Then, we can neglect again the 2nd term in
the difference in Eq. (61) with respect to the first one, and obtain,
accounting for the restrictions concerning
![]() ,
,
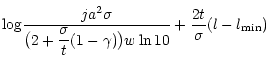 |
|||
| + | 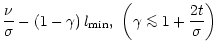 |
(70) | |
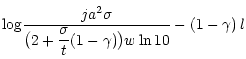 |
|||
| + | 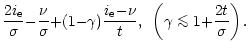 |
(71) |
These equations are similar to the case
![]() (Eqs. 66,
67), except from the offset and one decisive difference:
For line intensities larger than
(Eqs. 66,
67), except from the offset and one decisive difference:
For line intensities larger than ![]() ,
the line number is no longer
constant, but becomes directly coupled to the oscillator strength statistics
via the term
,
the line number is no longer
constant, but becomes directly coupled to the oscillator strength statistics
via the term
![]() .
Thus, a declining line number is expected for
.
Thus, a declining line number is expected for
![]() ,
whereas for
,
whereas for ![]() (slightly) larger than unity the
distribution function should increase. Note, that the predicted slope for
(slightly) larger than unity the
distribution function should increase. Note, that the predicted slope for
![]() is independent of temperature!
is independent of temperature!
Figure 9 impressively verifies our predictions. Here, we have
simulated an oscillator strength distribution with
![]() (left
panel), whereas in the middle one
(left
panel), whereas in the middle one
![]() was assumed. Note the
abrupt change in the slope at
was assumed. Note the
abrupt change in the slope at
![]() .
.
Finally, we consider the case of a rather steep gf-distribution
![]() ,
e.g.
,
e.g.
![]() for Fe II. Then, the
gf-distribution is dominated by its lower end, and the values taken at
for Fe II. Then, the
gf-distribution is dominated by its lower end, and the values taken at
![]() are dominating both the normalization constant and the difference
term, in contrast to the situation discussed above. Accordingly,
are dominating both the normalization constant and the difference
term, in contrast to the situation discussed above. Accordingly,
![]() and
and
![]() do no longer play any role, and we obtain a line number statistics
do no longer play any role, and we obtain a line number statistics
with uniform, temperature dependent slope ![]() .
Note, that the only
.
Note, that the only
![]() dependence shows up in the offset. The right panel in
Fig. 9 gives the corresponding result, for
dependence shows up in the offset. The right panel in
Fig. 9 gives the corresponding result, for
![]() and
and
![]() ,
which was used in order to obtain a statistically significant
number of lines at the high gf end. Obviously, no kink is present any
longer, and the distribution lies parallel to the low-
,
which was used in order to obtain a statistically significant
number of lines at the high gf end. Obviously, no kink is present any
longer, and the distribution lies parallel to the low-![]() part of
a corresponding (
part of
a corresponding (![]() = 1)-distribution, overplotted as rectangles.
= 1)-distribution, overplotted as rectangles.
So far, our investigations can be summarized as follows. Allan's approach
(extended for
![]() )
has been validated for a complex ion in those
cases when
)
has been validated for a complex ion in those
cases when ![]() is constant, and the slope of the distribution function
can be predicted: At low intensities (corresponding to high line-strengths),
it is controlled both by the level density as a function of excitation energy
(slope
is constant, and the slope of the distribution function
can be predicted: At low intensities (corresponding to high line-strengths),
it is controlled both by the level density as a function of excitation energy
(slope ![]() )
as well as by the population of these levels (excitation
temperature t), resulting from our LTE assumption. In this domain, the
oscillator strength distribution seems to be of no importance for the slope,
since - for
)
as well as by the population of these levels (excitation
temperature t), resulting from our LTE assumption. In this domain, the
oscillator strength distribution seems to be of no importance for the slope,
since - for
![]() - the line number is primarily
controlled by the highest gf-value, and for
- the line number is primarily
controlled by the highest gf-value, and for
![]() by the
lowest one, both of which do "only'' control the offset of the
distribution. For large line intensities (weak lines!), we encounter a
certain inter-relation between energetic neighbourhood to the ionization
limit and maximum possible gf-value (cf. Eq. 64), which causes a
slope dominated by the gf-distribution, provided
by the
lowest one, both of which do "only'' control the offset of the
distribution. For large line intensities (weak lines!), we encounter a
certain inter-relation between energetic neighbourhood to the ionization
limit and maximum possible gf-value (cf. Eq. 64), which causes a
slope dominated by the gf-distribution, provided ![]() is not too large.
In the opposite case, finally, the small gf-values become decisive over the
complete range, and the slope of the distribution retains its previous
slope for all
is not too large.
In the opposite case, finally, the small gf-values become decisive over the
complete range, and the slope of the distribution retains its previous
slope for all ![]() values.
values.
Thus, it seems that we have to know only the principal behaviour of
the gf-distribution to predict the LTE line intensity/line-strength statistics
for a certain ion. Unfortunately, Fig. 10
shows that this is at least not so simple. Here, we have plotted
![]() using the actual oscillator strengths. As is obvious, this
distribution looks rather different from the cases discussed so far, primarily
in the domain
using the actual oscillator strengths. As is obvious, this
distribution looks rather different from the cases discussed so far, primarily
in the domain
![]() .
.
 |
Figure 10: As Fig. 9, for T= 10000 K and actual gf-distribution |
 |
Figure 11:
Cumulative line number as function of
logarithmic oscillator strength r. Asterisks: Fe II, in the interval
|
The reason for this different functional behaviour becomes evident from Fig. 11, displaying the actual run of the oscillator strength distribution in the considered frequency interval as well as for "all'' lines of Fe II and all lines (for the atoms H to Zn, cf. Sect. 3.1) present in our data base.
At first note that the specific shapes of the particular distributions
are extremely similar, where the major differences concern the total line
number
![]() and the highest gf-value being present. In contrast to
the case of hydrogenic ions, however, the distribution does no longer show a
more or less constant slope, but is curved. At the high gf-end, the
distribution is rather steep, with an approximate slope
and the highest gf-value being present. In contrast to
the case of hydrogenic ions, however, the distribution does no longer show a
more or less constant slope, but is curved. At the high gf-end, the
distribution is rather steep, with an approximate slope
![]() over
the first 2.5 dex, and may be described afterwards again by the canonical
value
over
the first 2.5 dex, and may be described afterwards again by the canonical
value
![]() ,
before our line list becomes incomplete (for
,
before our line list becomes incomplete (for
![]() ). To our understanding, the steep increase results from the
very strong lines connecting the (effective) ground states with
low lying levels. These lines follow statistics different from the other
ones, a feature which we have also found in case of hydrogenic ions (cf.
also the related discussion in Allen [1966]).
). To our understanding, the steep increase results from the
very strong lines connecting the (effective) ground states with
low lying levels. These lines follow statistics different from the other
ones, a feature which we have also found in case of hydrogenic ions (cf.
also the related discussion in Allen [1966]).
Although the gf-distribution is significantly curved leading to certain
subtleties in the intensity distribution if considered in a specified
frequency range (as it was done, e.g., in
Fig. 10), it might be suspected that on a larger average
the description should become more uniform again. Note, e.g., that the
largest part of the distribution function (
![]() can be described by a more or less constant slope, with a
significantly steeper one only over the first two decades, which
consequently comprise only few lines.
can be described by a more or less constant slope, with a
significantly steeper one only over the first two decades, which
consequently comprise only few lines.
In order to check this hypothesis and to proceed towards our aim at
describing flux-weighted line-strength distribution functions under
stellar wind conditions, we will follow our analytical description assuming
constant slope ![]() .
From now on, however, we will concentrate on the
distribution of "all'' lines per ion, i.e., we will consider frequency
integrated distribution functions. Most important to this regard is the
frequency dependence of the threshold value
.
From now on, however, we will concentrate on the
distribution of "all'' lines per ion, i.e., we will consider frequency
integrated distribution functions. Most important to this regard is the
frequency dependence of the threshold value ![]() (Eq. 65), dividing
the two different domains of influence, namely either by excitation and/or
by gf-distribution. Since
(Eq. 65), dividing
the two different domains of influence, namely either by excitation and/or
by gf-distribution. Since ![]() decreases with frequency, lines with
higher frequencies (transitions from the lowest levels, dominating the
line-force) should be much more coupled to the oscillator strength
distribution than lines with lower frequencies.
decreases with frequency, lines with
higher frequencies (transitions from the lowest levels, dominating the
line-force) should be much more coupled to the oscillator strength
distribution than lines with lower frequencies.
After considering the limitations resulting from the frequency and
line intensity dependence of
![]() (cf. Eq. 64), the
distribution function Eq. (61) can be integrated over frequency, and
the result is given by
(cf. Eq. 64), the
distribution function Eq. (61) can be integrated over frequency, and
the result is given by
Summarizing the results concerning F derived in Appendix E, we
find that the frequency integrated distribution behaves rather similarly to
the frequency dependent one. In total,
three different slopes are possible, namely
![]() and
and ![]() ,
were the occurrence and position of the former two
are controlled by the value of
,
were the occurrence and position of the former two
are controlled by the value of ![]() being larger or smaller
than a critical value
being larger or smaller
than a critical value
![]() .
.
Under typical conditions, however, the function consists of only two parts,
namely a steeper, excitation-dominated one with slope ![]() ,
and a
second one with slope
,
and a
second one with slope ![]() ,
similar to the frequency dependent
distribution. The division is given at line intensity
,
similar to the frequency dependent
distribution. The division is given at line intensity
![]() ,
when we consider only those lines with a
lower energy level below the cutoff energy
,
when we consider only those lines with a
lower energy level below the cutoff energy
![]() introduced above.
Furthermore, in case of a frequency integration between 0 and
introduced above.
Furthermore, in case of a frequency integration between 0 and
![]() ,
the function preserves its shape for all
,
the function preserves its shape for all
![]() ,
an
effect which we have called the "saturation effect''.
,
an
effect which we have called the "saturation effect''.
In principle, the constant of proportionality in Eq. (73) depends
also on temperature and level distribution for the specified ion as
well as on the exponent of the oscillator-strength distribution. However,
in the following we derive this constant from the requirement that the total
line number is known (and to be found from the cumulative line number at
![]() ,
which is the maximum possible line intensity).
,
which is the maximum possible line intensity).
In order to check the validity and applicability of the above expressions, we have performed a number of test calculations in the same spirit in the previous section, i.e., for our atomic model of Fe II and simulating the gf-distribution by a Monte Carlo process.
 |
Figure 12:
Frequency integrated line intensity distribution functions of
Fe II at T = 15000 K. Frequency range
0 < x < 65 kK (see text) and
resolution 0.5 dex in intensity. Oscillator strengths simulated by Monte
Carlo with
|
 |
Figure 13:
As Fig. 12, using actual oscillator strengths
(asterisks). Overplotted is the analytical
result according to Eq. (73) with |
For our specific atomic model, we have
![]() kK (lines with
larger energies resulting from levels ionizing to excited levels of Fe
III were removed "by hand'' in order to simplify the test), and, from our
constraint of considering only those levels which under NLTE-conditions have
large enough occupation numbers to form lines of significant strength (see
Sect. 3.1 and next section), we have
kK (lines with
larger energies resulting from levels ionizing to excited levels of Fe
III were removed "by hand'' in order to simplify the test), and, from our
constraint of considering only those levels which under NLTE-conditions have
large enough occupation numbers to form lines of significant strength (see
Sect. 3.1 and next section), we have
![]() kK. For reasons of
consistency, the integration was performed in the corresponding range
kK. For reasons of
consistency, the integration was performed in the corresponding range
![]() kK. From a first comparison, it turned out that
kK. From a first comparison, it turned out that
![]() ,
which is also consistent with the average slope of the level
distribution. The normalization constant was chosen in such a way that a
total line number of
,
which is also consistent with the average slope of the level
distribution. The normalization constant was chosen in such a way that a
total line number of
![]() was reached in the considered frequency
range.
was reached in the considered frequency
range.
Since all other quantities defining the frequency integrated distribution
functions are given as parameters of the Monte Carlo simulation (
![]() ), a comparison of the analytical result and the
simulated line intensity distribution should coincide for all temperatures
and all values of
), a comparison of the analytical result and the
simulated line intensity distribution should coincide for all temperatures
and all values of ![]() ,
if the above expression were correct. An example
is given in Fig. 12, and the agreement is obvious, note in
particular the predicted steep slope for strong lines and the dependence of
the weak lines' distribution on
,
if the above expression were correct. An example
is given in Fig. 12, and the agreement is obvious, note in
particular the predicted steep slope for strong lines and the dependence of
the weak lines' distribution on ![]()
![]() .
.
In the next figure, we have investigated the most interesting question in
this respect, namely how far the analytical description can deal with the
real case. We have considered the same situation as above, however used
the actual oscillator strengths. Thus, by this comparison we can check
our hypothesis whether the frequency integrated distribution is less
influenced by curvature effects than the distribution defined at specific
frequencies, and ask for the effective ![]() -exponent of the
underlying oscillator strength distribution.
-exponent of the
underlying oscillator strength distribution.
Compared to the last simulations, we have changed only the parameters
![]() and
and
![]() in the analytical expression, and tried to fit the
actual distribution (asterisks) by varying the value of
in the analytical expression, and tried to fit the
actual distribution (asterisks) by varying the value of ![]() .
The choice
of the former quantities relates to the oscillator strength distribution
function of Fe II (Fig. 11, triangles), with a maximum
.
The choice
of the former quantities relates to the oscillator strength distribution
function of Fe II (Fig. 11, triangles), with a maximum
![]() -value (
-value (
![]() )
of 0.75 and the distribution becoming incomplete at
)
of 0.75 and the distribution becoming incomplete at
![]() .
Figure 13 gives the results for three
different values of
.
Figure 13 gives the results for three
different values of ![]() .
.
Two points are worth noticing. First, the actual distribution can be fitted
extremely well by our analytical approach (the same degree of precision was
reached at different temperatures), and the effective ![]() is of the
order 1.3, i.e., again representing the "canonical'' value. This is not too
surprising since a major part of the distribution actually follows this
slope (Fig. 11). Second, a comparison with the other simulations
with different
is of the
order 1.3, i.e., again representing the "canonical'' value. This is not too
surprising since a major part of the distribution actually follows this
slope (Fig. 11). Second, a comparison with the other simulations
with different ![]() illuminates the role of this
quantity: Although (and in agreement with our findings for the frequency
dependent line statistics) the slope of the distribution for strong lines
remains almost unaffected by
illuminates the role of this
quantity: Although (and in agreement with our findings for the frequency
dependent line statistics) the slope of the distribution for strong lines
remains almost unaffected by ![]() and is much more influenced by
temperature via excitation, the width of the distribution and its
vertical offset depend strongly on this quantity!
and is much more influenced by
temperature via excitation, the width of the distribution and its
vertical offset depend strongly on this quantity!
This behaviour is readily understood, if one remembers the
fact that ![]() primarily controls the distribution of weak lines: for
primarily controls the distribution of weak lines: for
![]() ,
the number of these lines remains constant (until
,
the number of these lines remains constant (until
![]() ),
whereas for
),
whereas for
![]() it decreases with increasing l and vice versa
for
it decreases with increasing l and vice versa
for
![]() .
This is not only true for frequency dependent distribution
functions but even more for integrated ones, since the threshold
line intensity
.
This is not only true for frequency dependent distribution
functions but even more for integrated ones, since the threshold
line intensity ![]() decreases with increasing frequency. The presence of
this effect is particularly demonstrated by our simulations for the high
temperature case shown here for this reason.
decreases with increasing frequency. The presence of
this effect is particularly demonstrated by our simulations for the high
temperature case shown here for this reason.
An additional constraint for the resulting distribution is the conservation
of total line number: If
![]() and the number of lines is small for
large l, this has to be compensated for by a larger number of lines at low
l. In contrast, for larger
and the number of lines is small for
large l, this has to be compensated for by a larger number of lines at low
l. In contrast, for larger ![]() and a consequently increasing number
of weak lines the number of strong lines has to be smaller. Finally, also
the width of the distribution at maximum
and a consequently increasing number
of weak lines the number of strong lines has to be smaller. Finally, also
the width of the distribution at maximum ![]() is affected, since this
region becomes flat for
is affected, since this
region becomes flat for
![]() ,
and the according width displays a
maximum.
,
and the according width displays a
maximum.
For reasons of brevity, we have presented here only the case of Fe II, due to its importance for radiative driving and its large number of lines leading to a low degree of statistical noise. Of course, we have checked our approach also for different ions (e.g., belonging to the CNO-group), and found a satisfactory agreement in any case.
Thus, the frequency integrated line intensity distribution of various ions can be described analytically assuming a power-law distribution for the gf-values, and we have illuminated the role of the corresponding exponent above.
The results presented here may turn out to be useful also in another regard.
Since the dependency of the frequency integrated line-intensity distribution
on the various parameters is understood, the procedure can be inverted
to check for the completeness of atomic data bases. This check can be easily
performed, since the calculation of the distribution function (per ion) is
simple, involving only Boltzmann excitation. From an analysis of the turn-over
points and the width of the distribution (as a function of input temperature),
it is thus possible to derive, e.g., the effective values of
![]() and
and
![]() ,
and data gaps will show up immediately.
By a variation of
,
and data gaps will show up immediately.
By a variation of
![]() ,
it will be also possible to constrain the
completeness as a function of frequency, at least in those cases where the
aforementioned "saturation effect'' does not play a role.
,
it will be also possible to constrain the
completeness as a function of frequency, at least in those cases where the
aforementioned "saturation effect'' does not play a role.
The next important step concerns the transition from line intensities to line-strengths, where we have the following relation (cf. Eq. (60) vs. 6):
Inserting typical parameters, this relation can be expressed as
Before we can relate the line intensity to the line-strength distribution function, we have to account for a parameter which is essential concerning this objective. Whereas for the (complete) distribution of line intensities all levels up to the ionization edge are significant (excitation by Boltzmann law), the line-strength distribution accounts for a lower number of levels and lines, namely those which are actually occupied under NLTE conditions. These are mainly those lines with a lower level attributed to one of the three categories defined in Sect. 3.1.2.
In other words, NLTE effects introduce an effective cutoff for contributing
(lower) levels,
![]() ,
already introduced in Eq. (73). As
discussed in Appendix E, this quantity (instead of the ionization potential
in the LTE-case) now controls the transition value between the excitation
vs. oscillator strength dominated part of the distribution function, i.e.,
this point is shifted significantly towards higher line-strengths. In
consequence, the apparent distribution resembles that of an ion with
low-lying ionisation potential! Of course, only part of this effect becomes
visible in the following, since the level lists in our data base have been
designed a priori to be complete only up to essentially occupied levels.
,
already introduced in Eq. (73). As
discussed in Appendix E, this quantity (instead of the ionization potential
in the LTE-case) now controls the transition value between the excitation
vs. oscillator strength dominated part of the distribution function, i.e.,
this point is shifted significantly towards higher line-strengths. In
consequence, the apparent distribution resembles that of an ion with
low-lying ionisation potential! Of course, only part of this effect becomes
visible in the following, since the level lists in our data base have been
designed a priori to be complete only up to essentially occupied levels.
An example for the correspondence of line-strengths vs. line intensities is
given in Fig. 14. The asterisks display the NLTE (Sect. 3.1)
line-strength distribution for Fe IV, and the fully drawn curve shows
the corresponding analytical line intensity distribution, however plotted as
a function of ![]() ,
with cutoff energy at
,
with cutoff energy at
![]() 170 kK (for
details, see caption). Note, that the highest level in our data base lies at
210 kK, and
170 kK (for
details, see caption). Note, that the highest level in our data base lies at
210 kK, and
![]() 440 kK.
440 kK.
From the perfect agreement, it is evident that the line-strength
distribution can be actually described in analogy to our previous results
for line intensities, where - in view of Eq. (76) - the "average''
shift is given by
![]() ,
and this shift
originates mainly from the rather low ionization fraction of Fe IV at
40000 K, of order 10-5. In this example, the distribution
is not "saturated'', i.e.,
,
and this shift
originates mainly from the rather low ionization fraction of Fe IV at
40000 K, of order 10-5. In this example, the distribution
is not "saturated'', i.e.,
![]() ,
which should lead to
two distinctive slopes in the first part of the distribution, namely
,
which should lead to
two distinctive slopes in the first part of the distribution, namely
![]() and
and ![]() (Appendix E). Even this subtle effect is
visible in the actual distribution!
(Appendix E). Even this subtle effect is
visible in the actual distribution!
As we have understood now, the distribution function per ion consists
of a steep and a flatter part, were the transition is controlled by the
ratio
![]() .
The major problem left is the summation over all
contributing ions, since, of course, each ion has its own specific Sjkvalue. Thus, even if the line intensities were similarly distributed
for each ion, the transformation (= horizontal shift) to the line-strength space might produce unpredictable results if all ions are
considered in parallel, as required, e.g., for the calculation of the
line-force.
.
The major problem left is the summation over all
contributing ions, since, of course, each ion has its own specific Sjkvalue. Thus, even if the line intensities were similarly distributed
for each ion, the transformation (= horizontal shift) to the line-strength space might produce unpredictable results if all ions are
considered in parallel, as required, e.g., for the calculation of the
line-force.
To facilitate the investigations, we have performed some test calculations before considering the real case, again by using the actual atomic models and NLTE occupation numbers (ionization and excitation have been calculated according to Sect. 3.1), however simulating the oscillator strength distribution via Monte Carlo.
Moreover, at first we have concentrated on ions with should behave rather
similarly due to their electronic structure (here: Ti to Cu, in the
following "iron group elements'', and later the "light ions'', C to Ca)
and assumed an equal abundance in order to distinguish between
ionization and abundance effects. The chosen abundance resembles the maximum
solar value for elements of the iron group, namely for Fe itself (
![]() ).
).
 |
Figure 15:
Asterisks: Line- strength distribution function for the
elements Ti to Cu (all ionization stages), with equal abundances
|
Figure 15 (asterisks) gives the resulting frequency
integrated line-strength distribution function for those iron group elements
and a simulated gf-distribution with
![]() and
and
![]() ,
for the same atmospheric conditions as in Fig. 14.
Obviously, three different groups are present, which can be easily
disentangled due to our knowledge of
,
for the same atmospheric conditions as in Fig. 14.
Obviously, three different groups are present, which can be easily
disentangled due to our knowledge of ![]() (input for Monte Carlo
simulation).
(input for Monte Carlo
simulation).
This is done in Fig. 16, by means of our analytical
description (Eq. 73) and at first in line intensity space. Note,
that the displayed solution is only one of a number of other possibilities:
For low-lying values of
![]() ,
which have been derived from the
onset of the flat
,
which have been derived from the
onset of the flat
![]() distribution and result from the effective
"NLTE cutoff''(here:
distribution and result from the effective
"NLTE cutoff''(here: ![]() 140 kK) and as long as the function is
"saturated'', which is the case in our example, the actual value of the
ionization energy is unimportant (cf. Eq. E8). Decisive is only the
parameter
140 kK) and as long as the function is
"saturated'', which is the case in our example, the actual value of the
ionization energy is unimportant (cf. Eq. E8). Decisive is only the
parameter ![]() ,
controlling the steeper part of the distribution
function via
,
controlling the steeper part of the distribution
function via
![]() .
.
 |
Figure 16:
Analytic line intensity distribution functions for the three components
visible in Fig. 15. Common parameters:
|
After summing up the three different components and plotting them as
a function of ![]() ,
the line-strength distribution found in
Fig. 15 (asterisks) can be easily simulated and is
displayed by the bold line in this figure. Thus, although the actual
function consists of a variety of contributing ions (at least 20 important
stages in the considered case), only a small number of clearly different
groups behaving similarly amongst each other is finally present. The
first group consists of dominant ionization stages (
,
the line-strength distribution found in
Fig. 15 (asterisks) can be easily simulated and is
displayed by the bold line in this figure. Thus, although the actual
function consists of a variety of contributing ions (at least 20 important
stages in the considered case), only a small number of clearly different
groups behaving similarly amongst each other is finally present. The
first group consists of dominant ionization stages (
![]() ),
the second one of minor stages comparable to Fe IV in
Fig. 14 (
),
the second one of minor stages comparable to Fe IV in
Fig. 14 (
![]() ), and the third one comprises the
weakest lines from ions with negligible populations (
), and the third one comprises the
weakest lines from ions with negligible populations (
![]() ).
Before commenting on this similarity in behaviour, let us firstly
demonstrate that our findings are not only by chance.
).
Before commenting on this similarity in behaviour, let us firstly
demonstrate that our findings are not only by chance.
Figure 17 shows the same situation as displayed in
Fig. 15 (asterisks), with the only change of ![]() from
1 to 0.8. Actually, even without simulating the new function, it is clear
that our argumentation still holds. Again, we can distinguish three groups,
and, consistent with our earlier findings, the plateaus from
Fig. 15 related to
from
1 to 0.8. Actually, even without simulating the new function, it is clear
that our argumentation still holds. Again, we can distinguish three groups,
and, consistent with our earlier findings, the plateaus from
Fig. 15 related to
![]() have changed into declining
slopes related to the new slope of
have changed into declining
slopes related to the new slope of
![]() .
If we now apply the
identical parameters as in Fig. 16 (accounting, of course,
for
.
If we now apply the
identical parameters as in Fig. 16 (accounting, of course,
for
![]() )
and overplot the summed result, we find again a
satisfactory agreement. This clearly indicates that the combination of
parameters chosen for the individual components are of the correct order,
and that the line-strength distribution function actually consists of three
different components, with similar effective cutoff energies.
)
and overplot the summed result, we find again a
satisfactory agreement. This clearly indicates that the combination of
parameters chosen for the individual components are of the correct order,
and that the line-strength distribution function actually consists of three
different components, with similar effective cutoff energies.
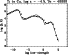 |
Figure 17:
As Fig. 15, however with exponent
|
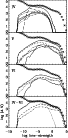 |
Figure 18:
Asterisks: Actual line-strength distribution function for the
elements Ti to Cu (all ionization stages), with equal abundances
|
Figure 18 (asterisks) displays now the actual case, i.e., without
any manipulation of the oscillator strengths. A comparison with the
![]() simulation (Fig. 15) shows that the differences are
only small: Again, three distinct distributions are visible, where the
transition from group one to two (roughly at
simulation (Fig. 15) shows that the differences are
only small: Again, three distinct distributions are visible, where the
transition from group one to two (roughly at
![]() )
is no
longer as pronounced as before. This might indicate that the actual
gf-distribution for the lines of this group is steeper than
)
is no
longer as pronounced as before. This might indicate that the actual
gf-distribution for the lines of this group is steeper than
![]() The second group, however, is consistent with
The second group, however, is consistent with
![]() ,
as
is obvious from the plateau at
,
as
is obvious from the plateau at
![]() .
.
The details of this figure give an the answer to the question raised above,
namely, why the sum of rather complex individual distributions (for the
dominant iron group ions at
![]() K, see caption) can
be described in such simple terms as above.
K, see caption) can
be described in such simple terms as above.
From the last panel, it is obvious that ionization stages V and VI represent the first group, and stage IV is identical with the second one. Additionally, from the sharp decline of the bold line (sum of stages IV, V, VI) at the end of the plateau, where the complete distribution function including all ions is rising again, it is clear that the third group (not analyzed here) consists of "real'' trace ions (mostly stage III).
The upper three panels show the distribution of the individual species amongst the various ionization stages (as well as the appropriate sums). Neglecting certain subtleties, all elements of a given ionization stage behave similarly. Thus, we can speak of line-strength distribution functions of specific ionization stages instead of individual ions (equal abundances provided).
The origin of this similarity bases on the only minor differences (in a
statistical sense) in atomic structure of the iron group elements under
consideration, especially with respect to ionization rates (giving rise to
similar ionization fractions), a rather low lying effective cutoff energy
and a level density parameter ![]() which is small enough to induce the
steep increase in the first part of the distribution. Note already here that
the according slope (the steeper one!) is roughly equal for all kinds of
ions and consequently also for the summed distributions, independent of
temperature (provided, of course, the abundances were equal). This equality
is clearly shown in Figs. 18, 19 and
20 and translates to a similarity in
which is small enough to induce the
steep increase in the first part of the distribution. Note already here that
the according slope (the steeper one!) is roughly equal for all kinds of
ions and consequently also for the summed distributions, independent of
temperature (provided, of course, the abundances were equal). This equality
is clearly shown in Figs. 18, 19 and
20 and translates to a similarity in
![]() ,
being of order unity. Since the value of 2t varies from 32 to
160 in the appropriate units (corresponding to 10000 ...50000 K), this
indicates that the (effective) level-density parameter
,
being of order unity. Since the value of 2t varies from 32 to
160 in the appropriate units (corresponding to 10000 ...50000 K), this
indicates that the (effective) level-density parameter ![]() (the
smaller, the steeper is the level-distribution as function of energy) has to
vary in concert with these numbers. With respect to the cases discussed
already as well as from the argument that an increase in ionization
stage/potential inevitably leads to an increase of
(the
smaller, the steeper is the level-distribution as function of energy) has to
vary in concert with these numbers. With respect to the cases discussed
already as well as from the argument that an increase in ionization
stage/potential inevitably leads to an increase of ![]() (fewer levels
distributed over a larger energy interval), this behaviour is not surprising
at all.
(fewer levels
distributed over a larger energy interval), this behaviour is not surprising
at all.
In addition to this similarity in excitation dominated slope, the
gf-distributions are similar as well, with ![]() between 1...1.3
(
between 1...1.3
(
![]() ), dominating the individual distributions
after the first two or three decades of steep incline.
), dominating the individual distributions
after the first two or three decades of steep incline.
In consequence, the total line-strength distribution has a "staircase''-like structure, where each staircase corresponds to a specific stage and is controlled by the sequence excitation/oscillator strength distribution. The horizontal width of these staircases depends mostly on the prevalent ionization fraction.
Since "only'' the first seven to ten decades of line-strength are important
for line-driving, only those trace ions do contribute to the total
distribution which have a significant ionization fraction (and abundance,
cf. Sect. 4.2.6) not below roughly
![]() as well as a larger number of lines than the dominant ionization species. In the other
case, i.e., if the line number is smaller, these trace ions are barely visible
in the summed distribution: Then, the
as well as a larger number of lines than the dominant ionization species. In the other
case, i.e., if the line number is smaller, these trace ions are barely visible
in the summed distribution: Then, the ![]() power-law increase of lines
from major species (which extends
power-law increase of lines
from major species (which extends
![]() decades in
line-strength from the turnover point to the "left'') dominates the
essential part of the distribution.
decades in
line-strength from the turnover point to the "left'') dominates the
essential part of the distribution.
Especially for iron group elements, the (total) line number per ion
increases strongly with decreasing ionization stage due to the increasing
complexity of electronic structure. Thus, at higher temperatures a
significant contribution from trace ions of lower stages is actually
possible, since these have the required larger line number. At the lower
temperature end of radiatively driven winds (roughly
![]() 8000 K), however, all (important) trace ions have necessarily a higher
degree of ionization than the major ones and consequently do not (or only
marginal) contribute to radiative driving.
8000 K), however, all (important) trace ions have necessarily a higher
degree of ionization than the major ones and consequently do not (or only
marginal) contribute to radiative driving.
This effect is clearly visible in Fig. 19, where we
have plotted the line-strength distribution for iron group elements (again
using equal abundances) as function of temperature. At the lowest
temperature displayed (
![]() 10000 K, bold line), the enormous line
number from ionization stages II and III dominates the first
twelve decades. Trace ions (below
10000 K, bold line), the enormous line
number from ionization stages II and III dominates the first
twelve decades. Trace ions (below
![]() )
have too few lines (as
well as negligible ionization fractions) to be of any importance. At
20000 K (dotted), the situation is slightly different. Here, stages
III and IV are essential, however a 2nd peak shows up indicating the
presence of stages II. This trend continues to higher temperatures,
e.g., for the case discussed above (
)
have too few lines (as
well as negligible ionization fractions) to be of any importance. At
20000 K (dotted), the situation is slightly different. Here, stages
III and IV are essential, however a 2nd peak shows up indicating the
presence of stages II. This trend continues to higher temperatures,
e.g., for the case discussed above (
![]() 40000 K, asterisks), two
kinds of trace ions become visible, namely stage IV in the middle part
and stage III with even more lines at weakest line-strengths. At the
highest temperature (
40000 K, asterisks), two
kinds of trace ions become visible, namely stage IV in the middle part
and stage III with even more lines at weakest line-strengths. At the
highest temperature (
![]() 50000 K, dashed-dotted), the dominant
species are VI and partly VII. Ions from stage V
contribute significantly, whereas stage IV with its typical
50000 K, dashed-dotted), the dominant
species are VI and partly VII. Ions from stage V
contribute significantly, whereas stage IV with its typical
![]() distribution is visible only at weakest line-strengths. Thus and in
total, we see a clear dominance of one or two major ionization species
in the complete temperature regime.
distribution is visible only at weakest line-strengths. Thus and in
total, we see a clear dominance of one or two major ionization species
in the complete temperature regime.
Let us now concentrate on the decisive part of the distribution
(down to, say,
![]() ). With decreasing temperature, the
maximum line-strength
). With decreasing temperature, the
maximum line-strength
![]() increases, which is primarily related
to the presence of low-lying meta-stable levels acting as quasi ground
states, which are missing in the higher ionization stages. Most
important, however, is the difference in total line-number! Whereas at the
hottest temperatures the transition point occurs at a line number
increases, which is primarily related
to the presence of low-lying meta-stable levels acting as quasi ground
states, which are missing in the higher ionization stages. Most
important, however, is the difference in total line-number! Whereas at the
hottest temperatures the transition point occurs at a line number
![]() ,
at lower temperatures a factor of 10 more lines are present at
this point. This difference, of course, bases on the increasing number of
lines with decreasing ionization stage
,
at lower temperatures a factor of 10 more lines are present at
this point. This difference, of course, bases on the increasing number of
lines with decreasing ionization stage
![]() (Eq. (61),
Allen ([1966]), his Eq. (3.6) and accounting for
(Eq. (61),
Allen ([1966]), his Eq. (3.6) and accounting for
![]() ).
Note, however, that the position of the transition point itself (
).
Note, however, that the position of the transition point itself (
![]() !)
and both slopes (before and after) remain essentially unaffected.
!)
and both slopes (before and after) remain essentially unaffected.
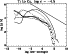 |
Figure 19:
Line-strength distribution function for the elements Ti to Cu,
with equal abundances
|
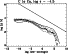 |
Figure 20:
As Fig. 19, however for the light ions
C to Ca and equal abundances
|
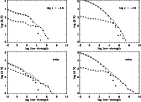
|
Figure 21:
Summing up the line-strength distribution functions for iron
group elements and light ions. Atmospheric parameters as in
Fig. 14, for a temperature of 40000 K (left) and 10000 K
(right panel).
Upper row: Distribution functions for iron group elements (asterisks) and
light ions, (triangles), assuming equal abundances
|
So far, we have concentrated on iron group elements. As we will see soon,
light ions play an equally important role, although the total number of
lines from those elements is significantly smaller. Figure 20
shows the corresponding line-strength distribution, again with equal
abundances and as function of temperature. In contrast to above, the maximum
value of ![]() remains rather constant, since the strongest lines are formed
by resonance transitions, so that excitation effects are unimportant for the
definition of
remains rather constant, since the strongest lines are formed
by resonance transitions, so that excitation effects are unimportant for the
definition of
![]() .
The largest differences occur at intermediate
line-strengths. They are connected to the large number of resonance lines
from lower ionization stages in the region around 600 Å(convergence to
ionization edges), whereas the corresponding lines of the higher stages are
situated well below our frequential cutoff at 250 Å. On the whole,
however, the distribution functions are much more similar when the
temperature is varied, compared to the iron group case, and the overall line
number is smaller everywhere. The reason for this difference is readily
understood, if we account for the vanishing number of meta-stable levels in
light ions, so that the group of lines with a meta-stable level as lower one
(which comprises the majority of lines for iron group elements) is
completely missing. Again, the excitation dominated part shows (virtually)
no reaction on temperature, i.e.,
.
The largest differences occur at intermediate
line-strengths. They are connected to the large number of resonance lines
from lower ionization stages in the region around 600 Å(convergence to
ionization edges), whereas the corresponding lines of the higher stages are
situated well below our frequential cutoff at 250 Å. On the whole,
however, the distribution functions are much more similar when the
temperature is varied, compared to the iron group case, and the overall line
number is smaller everywhere. The reason for this difference is readily
understood, if we account for the vanishing number of meta-stable levels in
light ions, so that the group of lines with a meta-stable level as lower one
(which comprises the majority of lines for iron group elements) is
completely missing. Again, the excitation dominated part shows (virtually)
no reaction on temperature, i.e.,
![]() as discussed above.
as discussed above.
In Fig. 21, we have added now the contribution of light and
heavy ions, both for the case of a hot wind at 40000 K as well as for a
rather "cool'' wind at 10000 K. Additionally, we study the influence of
accounting for realistic abundances, e.g., a solar mixture. Most
importantly, by giving up the uniform composition, the distribution function
of heavy elements is shifted to the left (to lower line-strengths), since
all contributing elements behave rather similarly (Fig. 18),
however the (solar) abundance of elements different from Fe is smaller than
the value
![]() adopted so far. Accordingly, the light
ions' distribution function is shifted (to a lesser extent) to the right
(
adopted so far. Accordingly, the light
ions' distribution function is shifted (to a lesser extent) to the right
(![]() larger than for Fe on the average).
larger than for Fe on the average).
Thus, the difference between maximum line-strengths is increased if a solar
composition is accounted for. The effect seems to be especially large for
the cooler wind, where
![]() (light ions) is increased by 2 dex:
At these temperatures, the Hydrogen Lyman
lines (and, to a lesser extent, the He II Lyman lines), which are
insignificant at hotter temperatures, show up at
largest line-strengths, both because of the larger ionization fraction of
neutral hydrogen (and He II) as well as their much higher abundance,
compared to the metals.
(light ions) is increased by 2 dex:
At these temperatures, the Hydrogen Lyman
lines (and, to a lesser extent, the He II Lyman lines), which are
insignificant at hotter temperatures, show up at
largest line-strengths, both because of the larger ionization fraction of
neutral hydrogen (and He II) as well as their much higher abundance,
compared to the metals.
Additionally, the resulting distribution functions (solar case) show even
less structure than in the case of uniform abundance, simply because there
is a larger scatter of the product
![]() (Eq. 75),
which leads to a larger variation of Sljk (Eq. 76) and
consequently to a smoothing of any inherent ("staircase'') structure which
is still visible in the case of uniform abundances (e.g.,
Fig. 20).
(Eq. 75),
which leads to a larger variation of Sljk (Eq. 76) and
consequently to a smoothing of any inherent ("staircase'') structure which
is still visible in the case of uniform abundances (e.g.,
Fig. 20).
Accounting now for these differences as a function of abundance as well as the intrinsic differences in the line statistics of iron group elements vs. light ions discussed previously, it becomes evident what controls the slope of the total line-strength distribution.
At first and for large line-strengths, the distribution is dominated by the
behaviour of light ions, and it is the steeper, excitation influenced part
of their distribution which plays the important role. Since a variety of
abundances is present, the distribution is smoother and wider (more, however
less pronounced staircases!). Thus, the according slope is flatter than
the value of unity found in the case of equal abundances. Since the local
slope translates to
![]() with
with
![]() ,
,
![]() becomes larger than zero in this domain (see also
Fig. 25). For a cool plasma, the influence of the
becomes larger than zero in this domain (see also
Fig. 25). For a cool plasma, the influence of the
![]() distribution of H (Sect. 4.1) flattens the curve additionally.
distribution of H (Sect. 4.1) flattens the curve additionally.
On the other hand, the left part of the distribution (low ![]() )
is
controlled by iron group elements, due to their much larger line number. To
obtain a situation where the light ions were of any influence in this range
would require a mixture with a very small abundance of heavy elements,
compared to the CNO group (Pop. III stars?).
)
is
controlled by iron group elements, due to their much larger line number. To
obtain a situation where the light ions were of any influence in this range
would require a mixture with a very small abundance of heavy elements,
compared to the CNO group (Pop. III stars?).
The specific influence of the solar composition (actually, only the ratio
and not the absolute numbers is relevant!) is evident from a comparison of
both rows in Fig. 21 and the corresponding dashed lines, giving
the total distribution functions. As discussed above, this abundance ratio
introduces a larger separation of the two components. If the abundances were
equal (upper row), the transition region between strong and weak
line-strengths controlled by the light and heavy ions, respectively, is
rather small. Thus, below the cutoff (effective
![]() !) of the light ions,
the distribution is suddenly dominated by the distribution of the
heavy elements with their much larger line number, and the steep slope
(order unity) of the first part of the total distribution function is
continued, until finally the gf-dominated part becomes visible.
!) of the light ions,
the distribution is suddenly dominated by the distribution of the
heavy elements with their much larger line number, and the steep slope
(order unity) of the first part of the total distribution function is
continued, until finally the gf-dominated part becomes visible.
For solar abundance ratios (lower row), the intermediate range is much
wider, and, accordingly, the transition to the flatter, gf-dominated part
from iron group elements occurs in a rather smooth way. In connection with
the fact that for a mixture of abundances the first part is flatter anyway,
we find
![]() for almost all
for almost all ![]() ,
since
,
since
![]() with s <
1 in the first part,
with s <
1 in the first part,
![]() with
with
![]() for the lowest contributing line-strengths and has values in between at
intermediate strengths.
for the lowest contributing line-strengths and has values in between at
intermediate strengths.
Again: If there were no difference in the abundance of light and heavy ions,
the total distribution function would be steeper (significantly smaller
![]() )
and much more curved compared to the solar case.
)
and much more curved compared to the solar case.
From Fig. 21 it becomes also clear why the derived
![]() values decrease for decreasing temperature (cf.
Table 2)
values decrease for decreasing temperature (cf.
Table 2)![]() . At lower temperatures (right panel), there are
simply more iron group lines present (esp. Fe II, III, IV), compared to
the rather constant line number of light ions. Thus, by lowering the
temperature, the line-distribution becomes progressively steeper, especially
at intermediate line-strengths, which reduces the corresponding
. At lower temperatures (right panel), there are
simply more iron group lines present (esp. Fe II, III, IV), compared to
the rather constant line number of light ions. Thus, by lowering the
temperature, the line-distribution becomes progressively steeper, especially
at intermediate line-strengths, which reduces the corresponding ![]() 's
(see also Sect. 5.1).
's
(see also Sect. 5.1).
One might now question in how far the underlying gf-distribution is of any importance for the final result, since it is much more the (relative) difference in abundance and especially in line number between iron group elements and light ions which leads to the "observed'' line statistics. Accordingly, it is much more the mixture of different contributing ions with different ionization fractions and abundances, which plays a role, whereas the gf-dominated part of any specific ionization stage becomes visible only at the lowest end of contributing line-strengths.
To answer the above question, we have simulated the line-strength statistics
resulting from different gf-distributions, again by Monte-Carlo, and compare
the outcome with the actual situation in Fig. 22, both for the
hotter and the cool wind. In contrast to the case of individual ions or to
the case of uniform abundances (e.g., Figs. 15 and
17), the slope of the distribution
in the decisive
![]() range seems to be almost unaffected by the
various gf-distributions, neglecting certain subtleties (e.g., the expected
presence of small staircases for
range seems to be almost unaffected by the
various gf-distributions, neglecting certain subtleties (e.g., the expected
presence of small staircases for
![]() )
which are insignificant for
any result derived from the cumulative distribution (Fig. 22, lower
panel).
)
which are insignificant for
any result derived from the cumulative distribution (Fig. 22, lower
panel).
What really differs, is the vertical offset of the different distributions,
where this offset is monotonically increasing for decreasing ![]() ,
and
the actual case (asterisks) is met almost precisely for
,
and
the actual case (asterisks) is met almost precisely for ![]() between
between
![]() K) and
K) and
![]() K),
in agreement with the average situation (Fig. 11). This behaviour
is readily understood if we remember the discussion at the end of
Sect. 4.2.2: In addition to controlling the slope of the weaker lines for
individual ions,
K),
in agreement with the average situation (Fig. 11). This behaviour
is readily understood if we remember the discussion at the end of
Sect. 4.2.2: In addition to controlling the slope of the weaker lines for
individual ions, ![]() controls the absolute line number
controls the absolute line number ![]() .
In
mathematical terms, this occurs via the
.
In
mathematical terms, this occurs via the ![]() -dependent normalization
constant in Eq. (61) (note, that
-dependent normalization
constant in Eq. (61) (note, that
![]() ). The physical
interpretation is given in the discussion referred to: If the number of weak
lines decreases for decreasing
). The physical
interpretation is given in the discussion referred to: If the number of weak
lines decreases for decreasing ![]() ,
the number of strong lines must
consequently grow. This is the effect we observe in Fig. 22.
,
the number of strong lines must
consequently grow. This is the effect we observe in Fig. 22.
Thus, the final role of ![]() is an important, however implicit one. Due
to its relevance for the vertical offset and with respect to derived
force-multiplier parameters, it is much more decisive for the value of
is an important, however implicit one. Due
to its relevance for the vertical offset and with respect to derived
force-multiplier parameters, it is much more decisive for the value of
![]() (or
(or ![]() )
than for the local slope
)
than for the local slope ![]() and consequently
and consequently
![]() .
.
Our final task in order to describe the radiative line acceleration is to
weight the line-strength distribution functions obtained so far by the
appropriate flux distribution
![]() .
This is done in
Fig. 23, both for the model with equal as well as with solar
abundances. With respect to the shape of the distribution, no dramatic
effects are encountered, if we compare the non-weighted distributions
(lines) with the corresponding flux-weighted ones (symbols). In terms of our
discussion in Appendix E concerning the "saturation'' effect, this is by no
means surprising. The major impact of flux-weighting is at moderate
line-strengths, where the weighted distribution becomes slightly flatter,
since a number of high-frequency resonance lines of minor ions are blended
out due to missing flux.
.
This is done in
Fig. 23, both for the model with equal as well as with solar
abundances. With respect to the shape of the distribution, no dramatic
effects are encountered, if we compare the non-weighted distributions
(lines) with the corresponding flux-weighted ones (symbols). In terms of our
discussion in Appendix E concerning the "saturation'' effect, this is by no
means surprising. The major impact of flux-weighting is at moderate
line-strengths, where the weighted distribution becomes slightly flatter,
since a number of high-frequency resonance lines of minor ions are blended
out due to missing flux.
The corresponding force-multiplier parameters
![]() and
and
![]() are displayed in Fig. 24 as iso-contours in dependence of
are displayed in Fig. 24 as iso-contours in dependence of
![]() and
and
![]() (see Eq. (26) and the according
derivative with respect to
(see Eq. (26) and the according
derivative with respect to
![]() ). Compared to our findings from the
last section, nothing new has to be added: For solar composition, the
resulting
). Compared to our findings from the
last section, nothing new has to be added: For solar composition, the
resulting
![]() values are much more constant and larger than for the
simulation with equal abundances. By inspection of the displayed values for
values are much more constant and larger than for the
simulation with equal abundances. By inspection of the displayed values for
![]() ,
we find that they are rather small (much lower than the value
of 1/3 found for hydrogenic trace ions), indicating the dominance of major
ionization stages and the frozen in ionization of stellar winds.
,
we find that they are rather small (much lower than the value
of 1/3 found for hydrogenic trace ions), indicating the dominance of major
ionization stages and the frozen in ionization of stellar winds.
In order to account for more realistic fluxes, we have calculated additionally the case of an irradiation by Kurucz fluxes (consistently used also in the ionization equilibrium). Although some quantitative differences become visible (which turn out to be important for a correct description of B-star winds, cf. Petrenz [1999]), the general effects are small and do not change any qualitative conclusion derived so far.
Since we have included now all ingredients required to calculate line-force
and force-multiplier parameters, we can come back to one of the problems
stated in Sect. 2, namely the difference of
![]() (derived from the
line-acceleration itself) and the local slope of the flux-weighted
distribution function,
(derived from the
line-acceleration itself) and the local slope of the flux-weighted
distribution function, ![]() .
In accordance with our analytical results
from Sects. 2.3.2 and 2.4, Fig. 25 displays the following,
by means of our
.
In accordance with our analytical results
from Sects. 2.3.2 and 2.4, Fig. 25 displays the following,
by means of our
![]() 40000 K model: For not too large
40000 K model: For not too large ![]() respectively
respectively ![]() ,
both numbers are fairly similar. At the steep end of the
distribution, however, where the local slope (symbols) becomes large
(excitation dominated part of light ions) and
,
both numbers are fairly similar. At the steep end of the
distribution, however, where the local slope (symbols) becomes large
(excitation dominated part of light ions) and
![]() converges to
small values (solar abundances) or values
converges to
small values (solar abundances) or values
![]() (equal abundances,
(equal abundances,
![]() ,
cf. Sect. 4.2.6) the effective force-multiplier
parameter
,
cf. Sect. 4.2.6) the effective force-multiplier
parameter
![]() remains positive (as it should, by definition). Thus,
even at large
remains positive (as it should, by definition). Thus,
even at large
![]() (i.e., in the outer wind part), the value of
(i.e., in the outer wind part), the value of
![]() remains much more constant as if it were coupled to the local
slope. Nevertheless, especially for equal abundances the decrease of
remains much more constant as if it were coupled to the local
slope. Nevertheless, especially for equal abundances the decrease of
![]() at large line-strengths is significant! This decrease in
at large line-strengths is significant! This decrease in
![]() can have severe consequences for low metallicity or thin winds,
as we will see in the following section.
can have severe consequences for low metallicity or thin winds,
as we will see in the following section.
![\begin{figure}\includegraphics[width=8cm,clip]{ds8655f23.eps}\end{figure}](/articles/aas/full/2000/01/ds8655/Timg553.gif) |
Figure 23:
Cumulative flux (times frequency) weighted line-strength
distribution function for atmospheric parameters as in Fig. 14
and
|
| |
Figure 25:
Comparison of
|
Copyright The European Southern Observatory (ESO)