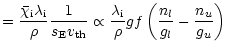 |
(D1) | ||
In LTE and using Kramer's formula, the hydrogen line-strength reads
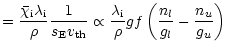 |
(D1) | ||
where n1 is the ground-state occupation number,
![]() are the
excitation energies of the lower and upper level, and the dependence on
the transition wavelength
are the
excitation energies of the lower and upper level, and the dependence on
the transition wavelength
![]() transforms into an additional power of
the second factor. Realizing that the appropriate variable for a further
expansion is given by
x=(n/n')3 < 1, and denoting
transforms into an additional power of
the second factor. Realizing that the appropriate variable for a further
expansion is given by
x=(n/n')3 < 1, and denoting
with ![]() the ground-state ionization energy and C' a factor absorbing
all "constants'' (most important:
the ground-state ionization energy and C' a factor absorbing
all "constants'' (most important: ![]() )
in the equation before,
we can write
)
in the equation before,
we can write
| = | |||
| = | 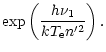 |
(D3) |
This equation can be expanded in powers of x, inverted and solved for n:
| = | 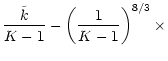 |
||
| = | 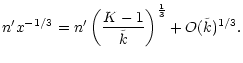 |
(D4) |
This expression is valid for not too large line-strengths
![]() .
Summing up again the number of lines with
line-strengths larger/equal than a given value, we finally obtain
the result given in (50),
.
Summing up again the number of lines with
line-strengths larger/equal than a given value, we finally obtain
the result given in (50),
Copyright The European Southern Observatory (ESO)