In this appendix, we want to discuss the relation between ![]() and Gayley's cut-off parameter
and Gayley's cut-off parameter
![]() .
In particular and
related to the discussion in Sect. 3.3, the inequality
.
In particular and
related to the discussion in Sect. 3.3, the inequality
![]() which has been found for cooler atmospheres shall be inspected.
which has been found for cooler atmospheres shall be inspected.
Using the definition of ![]() and the power-law line-strength distribution
with exponential cutoff, Eq. (B1),
and the power-law line-strength distribution
with exponential cutoff, Eq. (B1), ![]() can be expressed as
can be expressed as
| = | |||
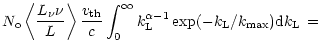 |
|||
| = | 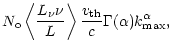 |
(C1) |
On the other hand, the flux (times frequency) weighted cumulative
line number, evaluted at maximum line-strength, gives
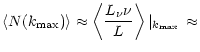 | |||
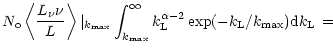 |
|||
| = | 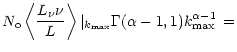 |
||
| = | 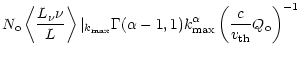 |
(C3) | |
| = | 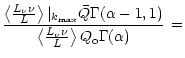 |
||
| = | 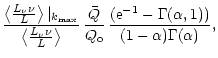 |
(C4) |
Thus, in cases where the frequential line-distribution is essentially
independent on line-strength and is distributed according to CAK's
assumption,
![]() and hence
and hence
![]() ,
,
![]() should
be (slightly) smaller than
should
be (slightly) smaller than ![]() ,
in contrast to what is "observed''
especially for cooler atmospheres. Vice versa, by accounting for the actual
similarity of
,
in contrast to what is "observed''
especially for cooler atmospheres. Vice versa, by accounting for the actual
similarity of ![]() and
and ![]() in hotter atmospheres (Table 2),
one might argue that the "effective'' number of lines with strength
in hotter atmospheres (Table 2),
one might argue that the "effective'' number of lines with strength ![]() shall be of order
shall be of order ![]() .
Independently from these more
"philosophical'' questions (involving uncertainties of order one dex), the
plain fact that the ratio
.
Independently from these more
"philosophical'' questions (involving uncertainties of order one dex), the
plain fact that the ratio
![]() is larger than unity and
increasing for decreasing
is larger than unity and
increasing for decreasing
![]() inevitably leads to the conclusion that
the average factor has to be significantly below unity and is decreasing in
parallel with
inevitably leads to the conclusion that
the average factor has to be significantly below unity and is decreasing in
parallel with
![]() .
Both by exploring
the frequential line-distribution of the strongest lines (cf.
Fig. 4 and the accompanying text) as well as by simply
calculating the average weight factor (Eq. C2), it turns out
that this is actually the case: for the same model atmospheres as in
Sect. 3.2, we find
.
Both by exploring
the frequential line-distribution of the strongest lines (cf.
Fig. 4 and the accompanying text) as well as by simply
calculating the average weight factor (Eq. C2), it turns out
that this is actually the case: for the same model atmospheres as in
Sect. 3.2, we find
![]() for
for
![]() K and
K and
![]() for
for
![]() K. Inserting these values and using the derived
K. Inserting these values and using the derived
![]() -values from Table 2,
-values from Table 2,
![]() = 0.35 and 28 are
predicted by means of (C5). The differences to the actual values of
1.16 and 16, respectively, remain to be attributed to the deviations from a
perfect power-law, especially at the predominantely contributing high
= 0.35 and 28 are
predicted by means of (C5). The differences to the actual values of
1.16 and 16, respectively, remain to be attributed to the deviations from a
perfect power-law, especially at the predominantely contributing high
![]() -end of the distribution.
-end of the distribution.
Copyright The European Southern Observatory (ESO)