- ...
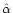
![[*]](/icons/foot_motif.gif)
- From here on, all line-force
parameters derived from a given or calculated force itself will be denoted
with an additional circumflex, in contrast to those parameters related or
resulting from a specific line statistics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... line-strength
![[*]](/icons/foot_motif.gif)
- The same result can be found by applying definition
(26) to our alternative expression for the line acceleration
(21), again independent from any assumption for the line
statistics. Note also, that Gayley ([1995]) defined the effective
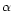 value at the critical point by the same expression.
value at the critical point by the same expression.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... balance
![[*]](/icons/foot_motif.gif)
- So far, we
have not been concerned with
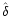 .
Before discussing this quantity
in Sect. 4.1, we anticipate that the variation of
.
Before discussing this quantity
in Sect. 4.1, we anticipate that the variation of
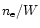 (for given t)
leads to a variation in total line number
(for given t)
leads to a variation in total line number
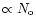 ,
which can be
described by
,
which can be
described by
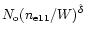 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field
![[*]](/icons/foot_motif.gif)
- We note that the inclusion or neglect of the very
strong, however somewhat peculiar (Sect. 4.2.6) hydrogen Lyman lines does
not affect the discussed discrepancy.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
hydrogen
![[*]](/icons/foot_motif.gif)
- If H I is a trace ion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... number
![[*]](/icons/foot_motif.gif)
- Under very specific conditions, the
effective
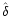 can even become negative.
can even become negative.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- A likewise agreement has
been found for simulations at T = 5000 and 10000 K.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...)
![[*]](/icons/foot_motif.gif)
- The argument given here remains also valid for
flux-weighted distribution functions, which are the actual basis for
deriving force-multipliers.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... outside
![[*]](/icons/foot_motif.gif)
- Only for the
CAK velocity law with exponent
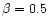 this value remains constant,
whereas the inclusion of the "finite disk correction factor (Friend &
Abbott [1986]; PPK) as well as the observations (Puls et al.
[1996]) give considerably larger values
this value remains constant,
whereas the inclusion of the "finite disk correction factor (Friend &
Abbott [1986]; PPK) as well as the observations (Puls et al.
[1996]) give considerably larger values
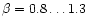 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
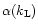
![[*]](/icons/foot_motif.gif)
- Actually,
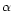 is not the local slope itself, however
is not the local slope itself, however
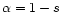 ,
if s is the negative exponent of the according
cumulative distribution function.
,
if s is the negative exponent of the according
cumulative distribution function.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ions
![[*]](/icons/foot_motif.gif)
- After this study has been finished, we
received a preprint by Vink et al. ([1999]) who have
investigated the so-called bi-stability jump in hot star winds. By
calculating the force-multipliers in a way similar to our approach, they
reached the same conclusions concerning the relative importance of iron
group elements vs. light ions with respect to
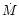 and
and
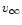 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.