| |
(46) |
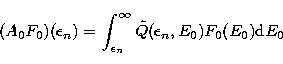 |
(47) |
We note that for both these approaches it is
necessary to
choose an explicit form for the average energy loss rate R(E). In the
case of a
collisional cold but ionized thick target characterized only by
Coulomb losses we have
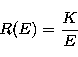 |
(48) |
If the determination of F0 is
addressed by solving
problem (5) the singular value decomposition can be performed in the
case of the
Kramers and the Bethe-Heitler approximations by computing the Gram matrix.
In the case of
the Kramers cross-section we find
 |
(49) |
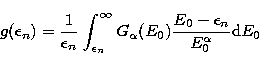 |
(50) |
 |
(51) |
![\begin{eqnarray}
G_{nm} & = & \frac{1}{\epsilon_n \epsilon_m} \left[ \frac{1}{2\...
..._m
\frac{1}{2\alpha-1}
\frac{1}{\epsilon_{n}^{2\alpha-1}} \right] \end{eqnarray}](/articles/aas/full/1998/17/ds7537/img104.gif) |
||
| (52) |
| Gnm=Gmn . | (53) |
![\begin{eqnarray}
g(\epsilon_n) &=& \frac{1}{\epsilon_n} \int_{\epsilon_n}^{\inft...
..._n}{E_0}}}{1-
\sqrt{1-\frac{\epsilon_n}{E_0}}}\right] {\rm d}E_0 .\end{eqnarray}](/articles/aas/full/1998/17/ds7537/img105.gif) |
||
| (54) |
![\begin{displaymath}
\phi_n(E_0) = \left\{ \begin{array}
{lr} 0 & E_0 \leq \epsil...
...{E_0}}}\right] \end{array} & E\gt\epsilon_n \end{array} \right.\end{displaymath}](/articles/aas/full/1998/17/ds7537/img106.gif) |
(55) |
 |
The condition numbers for the problems (50) and (54) are
presented in Table 2
and in Fig. 2 we plot the first four singular functions in the case of N=25
geometrically sampled points in the energy range ![]() keV,
keV,
![]() keV. As in
the case of the thin-target model, if the Bethe-Heitler cross-section is
adopted the
instability of the problem is greater and the resolution limit achievable
is poorer for prescribed solution accuracy.
keV. As in
the case of the thin-target model, if the Bethe-Heitler cross-section is
adopted the
instability of the problem is greater and the resolution limit achievable
is poorer for prescribed solution accuracy.
Copyright The European Southern Observatory (ESO)