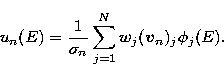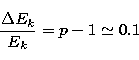Up: Optimal inversion of hard
Let us consider
Eq. (4) with a general form for the cross-section 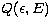 . In
practical applications the photon spectrum is known only at discrete values of
the photon energy and the equation we have to deal with is
. In
practical applications the photon spectrum is known only at discrete values of
the photon energy and the equation we have to deal with is
| 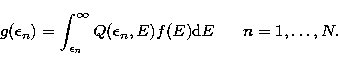 |
(11) |
Actually detectors provide integrals of
the spectrum over finite ranges of photon energy and a more realistic version
of the discrete equation is represented by Eq. (48) in
(Piana 1994).
However in that paper it was shown that as far as the inversion is concerned,
the difference between the use of point data and binned data is not
significant, though we need to allow for the effect of binning on photon count
statistics.
We assume that the function f belongs to the Hilbert space
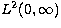 of the functions
of the functions 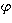 such that
such that 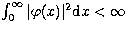 . The choice of this source space is for
mathematical reasons, though it is not physically unrealistic to assume that
the electron distribution functions are square integrable. We introduce the
integral operator
. The choice of this source space is for
mathematical reasons, though it is not physically unrealistic to assume that
the electron distribution functions are square integrable. We introduce the
integral operator 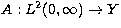 defined by
defined by
| 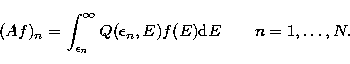 |
(12) |
Y is a finite dimension vector space
equipped with the inner product
| 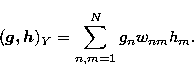 |
(13) |
The most suitable choice for
the weights wnm depends on the sampling adopted
(Bertero et al. 1984). For
example, in the case of the uniform sampling,
| 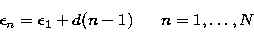 |
(14) |
with d constant, the
typical choice is
| 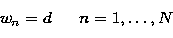 |
(15) |
while, in the case of the geometric sampling,
| 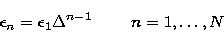 |
(16) |
with  a constant, it is usually
a constant, it is usually
| 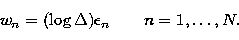 |
(17) |
Therefore the linear inverse problem with discrete data
(11) we are interested in can be described by the
equation
| 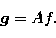 |
(18) |
We note that Riesz's
lemma
(Reed & Simon 1972) allows us to describe the action of the integral
operator by use of the scalar product 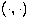 in
in 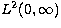 , i.e.
, i.e.
| 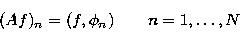 |
(19) |
with
| 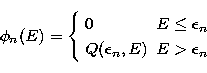 |
(20) |
for
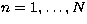 . We define the adjoint operator
. We define the adjoint operator 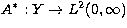 of A by
of A by
| 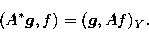 |
(21) |
Then the singular system of the
operator A is the set of triples 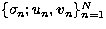 which solves the set of problems
(Bertero et al. 1985)
which solves the set of problems
(Bertero et al. 1985)
| 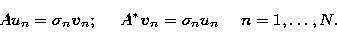 |
(22) |
The real non-negative numbers
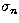 ,
, 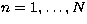 form a non-increasing sequence and are called
singular values, the functions un,
form a non-increasing sequence and are called
singular values, the functions un, 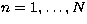 are called singular
functions and the vectors
are called singular
functions and the vectors 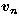 ,
, 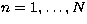 are called singular
vectors.
are called singular
vectors.
Knowledge of the singular system of the operator A is extremely
useful for the solution of the linear inverse problem with discrete data
(18). In particular:
- the singular system gives
information about the degree of instability of the solution of the inverse
problem;
- it represents a basic tool for the computation of regularization
algorithms providing approximate and stable solutions of the problem;
-
from the distribution of the zeros of the singular functions it is possible to
infer information about the resolution obtainable from the data.
Now we want to describe these three properties of the singular system in
detail.
If 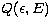 is the Kramers or Bethe-Heitler cross-section, the
linear inverse problem of determining the electron distribution function f
from the photon spectrum g when f and g are related by
Eq. (4) is ill-posed in the sense of Hadamard
(Hadamard 1923). A problem is
said well-posed in the sense of Hadamard if:
is the Kramers or Bethe-Heitler cross-section, the
linear inverse problem of determining the electron distribution function f
from the photon spectrum g when f and g are related by
Eq. (4) is ill-posed in the sense of Hadamard
(Hadamard 1923). A problem is
said well-posed in the sense of Hadamard if:
- the
solution of the problem exists for each data function.
- the solution is
unique;
- the solution depends continuously on the data.
If
at least one of these three requirements is not satisfied, the problem is
ill-posed in the sense of Hadamard. In the case of the inverse problem with
discrete data (18) the solution is clearly not unique - i.e., infinitely
many functions f yield precisely the same data vector 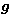 , though it can
be shown (Bertero 1989) that the problem of determining the solution among
these which has minimum norm (the so called generalized solution) is
well-posed. However, though the generalized solution of (18) is unique
for precisely given
, though it can
be shown (Bertero 1989) that the problem of determining the solution among
these which has minimum norm (the so called generalized solution) is
well-posed. However, though the generalized solution of (18) is unique
for precisely given 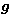 , it is unstable to noise on
, it is unstable to noise on 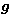 - that is the
problem is "ill-conditioned''. It can be shown that if
- that is the
problem is "ill-conditioned''. It can be shown that if 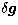 and
and
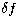 are respectively the error on the data and the error on the
(generalized) solution, the inequality
are respectively the error on the data and the error on the
(generalized) solution, the inequality
| 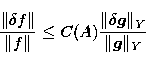 |
(23) |
holds. Here 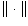 and
and 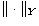 denote respectively
the norm in
denote respectively
the norm in 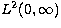 , i.e.
, i.e.
| 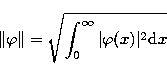 |
(24) |
and the
norm in Y, i.e.
| 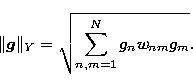 |
(25) |
The number C(A),
which depends on the explicit form of the operator A, is called the condition
number and clearly represents a reliable indicator of the (potential)
instability of the problem, for if C(A) is large from
Eq. (23) a
small relative error on the data may imply a significant relative error on the
solution. It can be shown that the relation
| 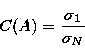 |
(26) |
holds, which shows that the singular
value spectrum of the operator carries explicit information about the
instability of the problem.
It is well-known that the numerical
instability of the solution of problem (18) can be reduced by applying
regularization. In the case of linear regularization methods a family of linear
operators 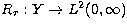 , with r the so-called
regularization parameter, is introduced and an approximate stable solution of
the problem is looked for in the set of regularized solutions
, with r the so-called
regularization parameter, is introduced and an approximate stable solution of
the problem is looked for in the set of regularized solutions 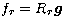 . The best of these regularized solutions is obtained by choosing an
optimum value of the regularization parameter r and to this aim "ad hoc''
criteria have been formulated
(Davies 1992). Examples of linear regularization
methods (Bertero 1989) are represented by Tikhonov's formulation, where
. The best of these regularized solutions is obtained by choosing an
optimum value of the regularization parameter r and to this aim "ad hoc''
criteria have been formulated
(Davies 1992). Examples of linear regularization
methods (Bertero 1989) are represented by Tikhonov's formulation, where
| 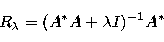 |
(27) |
and 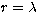 is real positive and by Landweber's iterative
formulation, where
is real positive and by Landweber's iterative
formulation, where
| 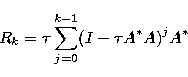 |
(28) |
with
| 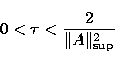 |
(29) |
and r=k is a positive integer (here
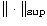 denotes the canonical operator norm). The computation of the
singular value decomposition of the operator A is basic for fast application
of both these methods since the action of the operators
denotes the canonical operator norm). The computation of the
singular value decomposition of the operator A is basic for fast application
of both these methods since the action of the operators 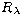 and Rk
can be described in terms of the singular system. In fact it can be shown that
and Rk
can be described in terms of the singular system. In fact it can be shown that
| 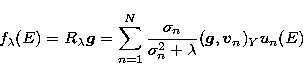 |
(30) |
and
| ![\begin{displaymath}
f_k(E)= R_{k} {\vec{g}} = \tau
\sum_{n=1}^{N} \frac{[1-(1-\t...
...sigma_{n}^{2})^k]}{\sigma_n}
({\vec{g}},{\vec{v}}_n)_Y u_n(E). \end{displaymath}](/articles/aas/full/1998/17/ds7537/img61.gif) |
(31) |
We note that also the computation
of the typical criteria for the choice of the regularization parameter is
simplified if the singular system of A is known
(Bertero 1989).
Knowledge of the behaviour of the singular functions also gives information
about the resolution achievable for given data and a given source space (in the
present case we have assumed 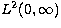 as the source space). In linear
inverse problem theory the concept of resolution limit is deeply related to a
concept called optimum choice of the experiment, meaning that
measurements are made in such a way as to give the maximum possible source
function resolution consistent with the limits imposed by noise. As already
pointed out, the minimum norm solution, or generalized solution, of problem
(18) exists and is unique; its expression in terms of the singular system
is
as the source space). In linear
inverse problem theory the concept of resolution limit is deeply related to a
concept called optimum choice of the experiment, meaning that
measurements are made in such a way as to give the maximum possible source
function resolution consistent with the limits imposed by noise. As already
pointed out, the minimum norm solution, or generalized solution, of problem
(18) exists and is unique; its expression in terms of the singular system
is
| 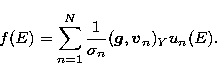 |
(32) |
If we increase the number of
experimental points N, the discretized problem (18) becomes closer and
closer to the continuous problem (4) and, as a consequence of the
ill-posedness of this problem and of the presence of noise on the data, the
generalized solution becomes more and more unstable. In other words, by adding
more points, we do not add more information and, even in the limiting case of
an infinite-dimensional problem, from a given data function, only a finite
amount of information can be derived. Obviously this finite amount of
information can be obtained with some finite number, say N0, of points.
Terminating sum (32) at N=N0 is optimal in that it recovers the full
information available while stabilizing the solution against random noise
variations. We could make the solution more stable by reducing N further, but
this has the price of reducing the information on resolution in the solution.
If the N0-th singular function has zeros, from
Eq. (32) the
generalized solution cannot contain details in intervals smaller than the
distance 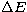 between adjacent zeros and the ratio
between adjacent zeros and the ratio  may be
adopted as a measure of the resolution corresponding to N0. In general the
optimum number N0 of points is not known and has to be chosen according to
how we decide to trade-off resolution versus instability. Let us then consider
the case of a noisy vector
may be
adopted as a measure of the resolution corresponding to N0. In general the
optimum number N0 of points is not known and has to be chosen according to
how we decide to trade-off resolution versus instability. Let us then consider
the case of a noisy vector 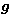 of N data points, with N>N0, and let us
apply, for example, Tikhonov's algorithm (30), in which high order terms
in (32) are increasingly suppressed rather than eliminated. In the case
of expansion (30) the number of singular functions which significantly
contribute to the restoration of the source function is in general less than
N. We denote this number again by N0. A possible criterion for choosing
N0 is that the relative error due to the truncation of the expansion
(30) must be just smaller than the measured relative error on
the photon
spectrum. Then the N0-th singular function is the last one giving a
significant contribution to the regularized solution defined in (30).
If
of N data points, with N>N0, and let us
apply, for example, Tikhonov's algorithm (30), in which high order terms
in (32) are increasingly suppressed rather than eliminated. In the case
of expansion (30) the number of singular functions which significantly
contribute to the restoration of the source function is in general less than
N. We denote this number again by N0. A possible criterion for choosing
N0 is that the relative error due to the truncation of the expansion
(30) must be just smaller than the measured relative error on
the photon
spectrum. Then the N0-th singular function is the last one giving a
significant contribution to the regularized solution defined in (30).
If 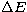 is the distance between the zeros of the N0-th singular
function so chosen,
is the distance between the zeros of the N0-th singular
function so chosen,  is the corresponding resolution limit (with
"higher resolution'' meaning smaller
is the corresponding resolution limit (with
"higher resolution'' meaning smaller  ).
).
The computation of
the singular system of the operator A is based on the observation (cf.
Eq. (22)) that the singular values and the singular vectors are
given respectively by the square root of the eigenvalues and by the
eigenvectors of the matrix AA*. Furthermore it can be proven that
(Bertero et al. 1985)
where
W is the weight matrix whose mn entry is defined by
| 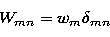 |
(34) |
and G is
the Gram matrix whose mn entry is defined by
| 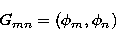 |
(35) |
with the functions 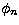 ,
,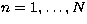 defined as in (20).
defined as in (20).
If we adopt the Kramers
cross-section the explicit form of the functions 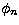 is given by
is given by
| 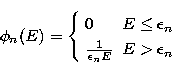 |
(36) |
and the mn entry of the Gram matrix is, for 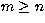
| 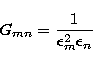 |
(37) |
and for m<n
If we adopt the Bethe-Heitler approximation, the explicit form
of the functions 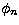 is given by
(Piana 1994)
is given by
(Piana 1994)
| 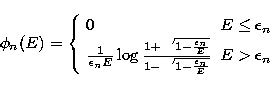 |
(39) |
and the mn entry of
the Gram matrix is, for m>n:
| 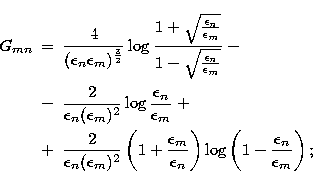 |
|
| |
| (40) |
for m=n:
| 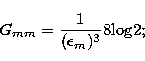 |
(41) |
for m<n:
In Table 1 we present the values of the condition number for
N=10,25,50,100 geometrically sampled points in the energy range 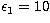 keV,
keV, 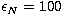 keV in the case of the Kramers and Bethe-Heitler
cross-sections. From these results the following facts can be deduced:
keV in the case of the Kramers and Bethe-Heitler
cross-sections. From these results the following facts can be deduced:
- for both cross-sections the condition number increases
with the number of sampling points. This behaviour can be explained by
observing that in the limit
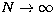 the finite rank operator
defined in (19) tends to the integral operator defined by the right hand
side of Eq. (4). This operator is compact and its singular spectrum
tends to zero. More roughly speaking, if the number of sampling points
increases, the discrete ill-conditioned problem becomes more and more similar
to the continuous problem which is ill-posed and whose ill-conditioning is
formally infinite;
the finite rank operator
defined in (19) tends to the integral operator defined by the right hand
side of Eq. (4). This operator is compact and its singular spectrum
tends to zero. More roughly speaking, if the number of sampling points
increases, the discrete ill-conditioned problem becomes more and more similar
to the continuous problem which is ill-posed and whose ill-conditioning is
formally infinite;
- the condition number is systematically bigger if the
Bethe-Heitler cross-section is adopted instead of the Kramers one because the
former is a smoother kernel. This means that in the case of the Bethe-Heitler
cross-section the inverse problem of determining the electron distribution
function from the photon spectrum is more unstable in the presence of data
noise. The factor of 10 increase in C(A) for N=25 data points, for
example, implies that the data accuracy needed for the recovery of the electron
spectrum with prescribed accuracy is 10 times higher when the Bethe-Heitler
formula is used.
Table 1:
Condition numbers for the thin-target
model in the case of the Kramers (K) and the Bethe-Heitler  approximations
for different numbers N of sampling points. The photon energy range is
approximations
for different numbers N of sampling points. The photon energy range is
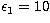 keV,
keV, 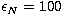 keV and the sampling is geometric
keV and the sampling is geometric
|
|
![\begin{figure}
\begin{center}
\includegraphics [height=13cm,clip=]{fig1.eps}
\end{center}\end{figure}](/articles/aas/full/1998/17/ds7537/Timg79.gif) |
Figure 1:
Singular functions for the thin-target model in the case of the
Kramers (solid) and the Bethe-Heitler (dashes) cross-section: a) first
singular function; b) second singular function; c) third singular
function; (4) fourth singular function |
In Fig. 1 the first four singular functions in the cases of
the Kramers and Bethe-Heitler cross-sections' are plotted for N=25
geometrically sampled points and energy range between 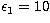 keV and
keV and
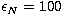 keV. These singular functions are computed by using the
formula
keV. These singular functions are computed by using the
formula
| 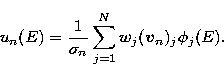 |
(43) |
We note that the singular functions
in the Kramers case are discontinuous at 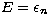
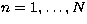 (they are
linear combinations of the functions
(they are
linear combinations of the functions 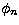 in (36) which are
discontinuous at these energies). Furthermore, for both approximations, the
singular function of order n is characterized by n zeros, approximately
displaced according to a geometric progression of ratio p. For a given data
vector
in (36) which are
discontinuous at these energies). Furthermore, for both approximations, the
singular function of order n is characterized by n zeros, approximately
displaced according to a geometric progression of ratio p. For a given data
vector 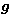 (and for a given source space) the value of p in the last
significant singular function (i.e., giving a significant contribution
to Eq. (30)), describes the achievable resolution limit. Therefore the
value of this limit explicitly depends on the level of noise affecting the
data. However it is possible to roughly foresee the difference in the
resolution limit achievable for the Kramers or the Bethe-Heitler
approximations. For example, let us take N=25 points geometrically sampled
between
(and for a given source space) the value of p in the last
significant singular function (i.e., giving a significant contribution
to Eq. (30)), describes the achievable resolution limit. Therefore the
value of this limit explicitly depends on the level of noise affecting the
data. However it is possible to roughly foresee the difference in the
resolution limit achievable for the Kramers or the Bethe-Heitler
approximations. For example, let us take N=25 points geometrically sampled
between 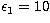 keV and
keV and 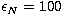 keV. In the Kramers approximation, the
condition number for 25 points is
keV. In the Kramers approximation, the
condition number for 25 points is 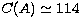 and the value of p for
the 25-th singular function is
and the value of p for
the 25-th singular function is 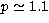 . It follows that the zeros of
the 25-th singular function occur at
. It follows that the zeros of
the 25-th singular function occur at
| 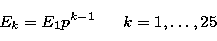 |
(44) |
so that
| 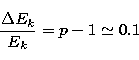 |
(45) |
is the resolution limit
(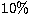 ). In the Bethe-Heitler approximation the condition number for 25
points is larger (
). In the Bethe-Heitler approximation the condition number for 25
points is larger (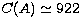 ). However, if we reduce the number of
points used in the Bethe-Heitler case, we find that the ratio
). However, if we reduce the number of
points used in the Bethe-Heitler case, we find that the ratio
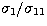 is approximately equal to the condition number in the
Kramers cross-section case for all 25 points (i.e.,
is approximately equal to the condition number in the
Kramers cross-section case for all 25 points (i.e., 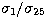 in the Kramers cross-section case). For the eleventh Bethe-Heitler singular
function the value of p is
in the Kramers cross-section case). For the eleventh Bethe-Heitler singular
function the value of p is  and in this case
and in this case 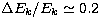 . From this we conclude that the resolution in the Kramers
cross-section approximation is double that for the Bethe-Heitler, for the same
solution accuracy.
. From this we conclude that the resolution in the Kramers
cross-section approximation is double that for the Bethe-Heitler, for the same
solution accuracy.


Up: Optimal inversion of hard
Copyright The European Southern Observatory (ESO)
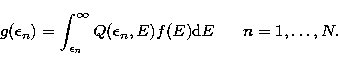
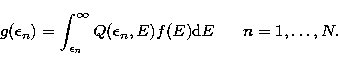
![]() of the functions
of the functions ![]() such that
such that ![]() . The choice of this source space is for
mathematical reasons, though it is not physically unrealistic to assume that
the electron distribution functions are square integrable. We introduce the
integral operator
. The choice of this source space is for
mathematical reasons, though it is not physically unrealistic to assume that
the electron distribution functions are square integrable. We introduce the
integral operator ![]() defined by
defined by
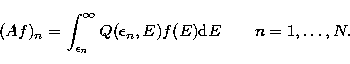
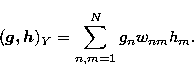
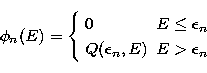
![]() is the Kramers or Bethe-Heitler cross-section, the
linear inverse problem of determining the electron distribution function f
from the photon spectrum g when f and g are related by
Eq. (4) is ill-posed in the sense of Hadamard
(Hadamard 1923). A problem is
said well-posed in the sense of Hadamard if:
is the Kramers or Bethe-Heitler cross-section, the
linear inverse problem of determining the electron distribution function f
from the photon spectrum g when f and g are related by
Eq. (4) is ill-posed in the sense of Hadamard
(Hadamard 1923). A problem is
said well-posed in the sense of Hadamard if: 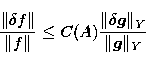
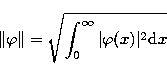
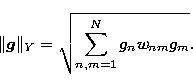
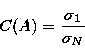
![]() , with r the so-called
regularization parameter, is introduced and an approximate stable solution of
the problem is looked for in the set of regularized solutions
, with r the so-called
regularization parameter, is introduced and an approximate stable solution of
the problem is looked for in the set of regularized solutions ![]() . The best of these regularized solutions is obtained by choosing an
optimum value of the regularization parameter r and to this aim "ad hoc''
criteria have been formulated
(Davies 1992). Examples of linear regularization
methods (Bertero 1989) are represented by Tikhonov's formulation, where
. The best of these regularized solutions is obtained by choosing an
optimum value of the regularization parameter r and to this aim "ad hoc''
criteria have been formulated
(Davies 1992). Examples of linear regularization
methods (Bertero 1989) are represented by Tikhonov's formulation, where
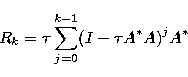
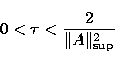
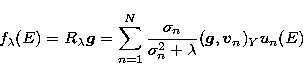
![\begin{displaymath}
f_k(E)= R_{k} {\vec{g}} = \tau
\sum_{n=1}^{N} \frac{[1-(1-\t...
...sigma_{n}^{2})^k]}{\sigma_n}
({\vec{g}},{\vec{v}}_n)_Y u_n(E). \end{displaymath}](/articles/aas/full/1998/17/ds7537/img61.gif)
![]() as the source space). In linear
inverse problem theory the concept of resolution limit is deeply related to a
concept called optimum choice of the experiment, meaning that
measurements are made in such a way as to give the maximum possible source
function resolution consistent with the limits imposed by noise. As already
pointed out, the minimum norm solution, or generalized solution, of problem
(18) exists and is unique; its expression in terms of the singular system
is
as the source space). In linear
inverse problem theory the concept of resolution limit is deeply related to a
concept called optimum choice of the experiment, meaning that
measurements are made in such a way as to give the maximum possible source
function resolution consistent with the limits imposed by noise. As already
pointed out, the minimum norm solution, or generalized solution, of problem
(18) exists and is unique; its expression in terms of the singular system
is
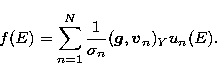
![]() is given by
is given by
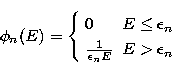
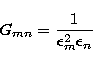
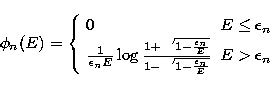
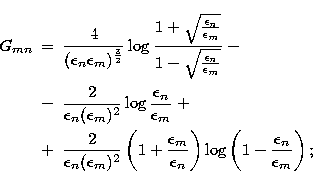
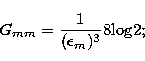
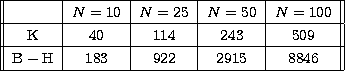
![]() keV and
keV and
![]() keV. These singular functions are computed by using the
formula
keV. These singular functions are computed by using the
formula