

Up: Optimal inversion of hard
We consider the analysis of solar flare hard X-rays (HXR) in the energy
range from around
ten to a few hundred keV emitted by collisional bremsstrahlung of high
energy electrons
on ions of the ambient plasma. We assume that the electron distribution
function is
isotropic and the hydrogen dominated plasma
is fully ionized (cf. discussion of the
latter by Brown et al. 1998). It is well-known that HXRs carry detailed
information
about flare electrons and, in particular, the shape of the spectra are
related to
electron acceleration and energy transport. Careful consideration of
techniques for
optimal recovery of such information is particularly timely with NASA's
planned launch of
the HESSI flare mission, the first to carry a high resolution HXR
spectrometer. Through
the 1960s and 70s only low spectral HXR resolution (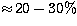 ) was
available
and without any spatial resolution. The 1980s and 90s saw the first HXR imaging
(SMM, Hinotori and YohKoh missions) and the separate advent of Ge detector
applications
yielding HXR resolution to
) was
available
and without any spatial resolution. The 1980s and 90s saw the first HXR imaging
(SMM, Hinotori and YohKoh missions) and the separate advent of Ge detector
applications
yielding HXR resolution to  . The latter allowed the first
possibility of
genuine HXR spectral inversion while the former gave the first indications
of the HXR
source structure. HESSI is the first instrument to combine both these
functions and
will enable new insight into the spectral distibution of source electrons
as functions of
position and time, facts of major interest to flare modelling. To obtain
the maximum
benefit from these data will require the development of optimal methods for
deconvolving
the observed photon spectra as well as the spatial information obtained by
the Fourier
imaging technique involved.
. The latter allowed the first
possibility of
genuine HXR spectral inversion while the former gave the first indications
of the HXR
source structure. HESSI is the first instrument to combine both these
functions and
will enable new insight into the spectral distibution of source electrons
as functions of
position and time, facts of major interest to flare modelling. To obtain
the maximum
benefit from these data will require the development of optimal methods for
deconvolving
the observed photon spectra as well as the spatial information obtained by
the Fourier
imaging technique involved.
In the case of an optically thin source of collisional bremsstrahlung, the
total rate of
photon emission  per unit photon energy
per unit photon energy 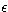 is given by
is given by
|  |
(1) |
where V is the volume of the emitting region,  is the density
of the ions
in the plasma,
is the density
of the ions
in the plasma,  is the local electron flux spectrum, E is the
electron energy and
is the local electron flux spectrum, E is the
electron energy and 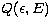 is the bremsstrahlung cross-section. We
note that g
represents the output at the sun while actual measurements are of the output
at the earth but
since only the shape of the spectrum and the relative errors are considered
here,
multiplicative constants are irrelevant.
is the bremsstrahlung cross-section. We
note that g
represents the output at the sun while actual measurements are of the output
at the earth but
since only the shape of the spectrum and the relative errors are considered
here,
multiplicative constants are irrelevant.
In a non-thermal atmosphere, Eq. (1) can be simplified
according to two different models. If the electron lifetimes inside the
source region are long compared to the observation time, then
 is not modified by energy loss and reflects the instantaneous flux
spectrum of high-energy electrons. In this non-thermal thin-target model
(Brown 1971) by defining the average ion density
is not modified by energy loss and reflects the instantaneous flux
spectrum of high-energy electrons. In this non-thermal thin-target model
(Brown 1971) by defining the average ion density
| 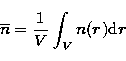 |
(2) |
and the average electron distribution function
|  |
(3) |
equation (1) can be simplified to
|  |
(4) |
If the lifetimes of the electrons in the source region are short compared
to the observation time, then electrons have to be continuously injected at
a rate  per unit injection energy E0. Within this
non-thermal thick-target framework the photon flux is given by
(Brown 1971)
per unit injection energy E0. Within this
non-thermal thick-target framework the photon flux is given by
(Brown 1971)
| 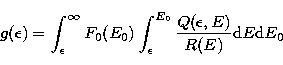 |
(5) |
where R(E) represents the average collisional energy loss rate of an
electron of energy E per unit plasma column density. Equation (5)
can be written in the form of a Volterra integral equation of the first
kind
| 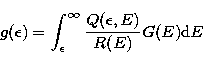 |
(6) |
by defining
|  |
(7) |
Both these models involve linear integral equations of the first kind,
where the data are represented by the continuous bremsstrahlung
spectrum and the solutions are energetic electron distribution functions - the
electron average distribution function f(E) or the injection rate
F0(E0). To find these functions from Eqs. (4)-(7)
an explicit
form for the bremsstrahlung cross-section 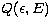 must be chosen. For
typical
applications (
must be chosen. For
typical
applications (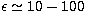 keV) non-relativistic expressions are
often adequate.
The simplest form is given
by Kramers' formula
(Koch & Motz 1959)
keV) non-relativistic expressions are
often adequate.
The simplest form is given
by Kramers' formula
(Koch & Motz 1959)
| 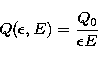 |
(8) |
where for hydrogen
| 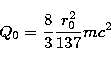 |
(9) |
with r0 the classical radius and m the rest mass of the electron
respectively.
A more accurate approximation is given by the Bethe-Heitler formula
| 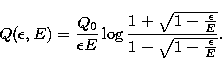 |
(10) |
However relativistic and semi-relativistic corrections have also been
introduced
(Gould 1980;
Haug 1997) and, in general, the sensitivity of the solutions
of Eqs. (4) or (5) to variations in the cross-section is an
interesting and important problem (see results below).
Inversion of Eq. (4), with the
Bethe-Heitler cross-section only, has been addressed
in (Piana 1994). In that paper the ill-posed
nature of the problem of determining f(E) from knowledge of
 was discussed and Tikhonov regularized versions of the
solution were
computed by using the singular system of the integral operator in the case
of discrete
data. Applications to noisy simulated and real spectra were also
considered. In the
present paper we want to generalize the singular value decomposition (SVD)
approach to
the case of non-thermal bremsstrahlung for both thick and thin targets and
for both forms
of Q above. Our aim is to provide a quantitative basis, in terms of SVD
analysis, for
evaluation of the differences resulting from the two cross-section
approximations, and
between the thick- and thin-target cases, in respect of the ill-posedness of the
problems, i.e., how accurately the source functions can be recovered from
noisy data in
each case. In Sect. 4 we compare these results with the analogous
ones for the more ill-posed problem of thermal bremsstrahlung inversion.
In a forthcoming paper, devoted to applications, we will use the
SVD analysis
to invert a real HXR spectrum emitted during a solar flare.
was discussed and Tikhonov regularized versions of the
solution were
computed by using the singular system of the integral operator in the case
of discrete
data. Applications to noisy simulated and real spectra were also
considered. In the
present paper we want to generalize the singular value decomposition (SVD)
approach to
the case of non-thermal bremsstrahlung for both thick and thin targets and
for both forms
of Q above. Our aim is to provide a quantitative basis, in terms of SVD
analysis, for
evaluation of the differences resulting from the two cross-section
approximations, and
between the thick- and thin-target cases, in respect of the ill-posedness of the
problems, i.e., how accurately the source functions can be recovered from
noisy data in
each case. In Sect. 4 we compare these results with the analogous
ones for the more ill-posed problem of thermal bremsstrahlung inversion.
In a forthcoming paper, devoted to applications, we will use the
SVD analysis
to invert a real HXR spectrum emitted during a solar flare.


Up: Optimal inversion of hard
Copyright The European Southern Observatory (ESO)
![]() per unit photon energy
per unit photon energy ![]() is given by
is given by

![]() is not modified by energy loss and reflects the instantaneous flux
spectrum of high-energy electrons. In this non-thermal thin-target model
(Brown 1971) by defining the average ion density
is not modified by energy loss and reflects the instantaneous flux
spectrum of high-energy electrons. In this non-thermal thin-target model
(Brown 1971) by defining the average ion density
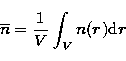


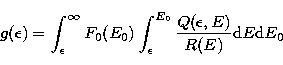
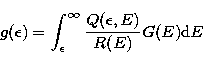

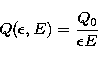
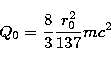
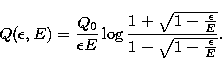
![]() was discussed and Tikhonov regularized versions of the
solution were
computed by using the singular system of the integral operator in the case
of discrete
data. Applications to noisy simulated and real spectra were also
considered. In the
present paper we want to generalize the singular value decomposition (SVD)
approach to
the case of non-thermal bremsstrahlung for both thick and thin targets and
for both forms
of Q above. Our aim is to provide a quantitative basis, in terms of SVD
analysis, for
evaluation of the differences resulting from the two cross-section
approximations, and
between the thick- and thin-target cases, in respect of the ill-posedness of the
problems, i.e., how accurately the source functions can be recovered from
noisy data in
each case. In Sect. 4 we compare these results with the analogous
ones for the more ill-posed problem of thermal bremsstrahlung inversion.
In a forthcoming paper, devoted to applications, we will use the
SVD analysis
to invert a real HXR spectrum emitted during a solar flare.
was discussed and Tikhonov regularized versions of the
solution were
computed by using the singular system of the integral operator in the case
of discrete
data. Applications to noisy simulated and real spectra were also
considered. In the
present paper we want to generalize the singular value decomposition (SVD)
approach to
the case of non-thermal bremsstrahlung for both thick and thin targets and
for both forms
of Q above. Our aim is to provide a quantitative basis, in terms of SVD
analysis, for
evaluation of the differences resulting from the two cross-section
approximations, and
between the thick- and thin-target cases, in respect of the ill-posedness of the
problems, i.e., how accurately the source functions can be recovered from
noisy data in
each case. In Sect. 4 we compare these results with the analogous
ones for the more ill-posed problem of thermal bremsstrahlung inversion.
In a forthcoming paper, devoted to applications, we will use the
SVD analysis
to invert a real HXR spectrum emitted during a solar flare.