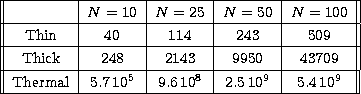Up: Optimal inversion of hard
For completeness and comparison we also give here (based on
Piana et al. 1995) the parallel analysis of the thermal inverse problem where
the emission is assumed to come from an optically thin thermal source
(Craig & Brown 1976). If 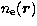 ,
,  are
the electron density and temperature at the point
are
the electron density and temperature at the point 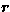 in the source
region and
in the source
region and 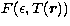 is the photon spectral distribution
function for an isothermal source
element, the photon spectrum is given by
is the photon spectral distribution
function for an isothermal source
element, the photon spectrum is given by
| 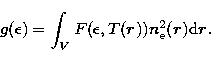 |
(56) |
From this equation, once the Kramers' cross-section is adopted and via
suitable changes of variable
(Craig & Brown 1976) we have
|  |
(57) |
where k is the Boltzmann constant and  is the differential
emission measure defined by
is the differential
emission measure defined by
|  |
(58) |
with  a constant temperature surface.
a constant temperature surface.
Equation (57) can be
easily transformed into the inverse Laplace transform problem
| 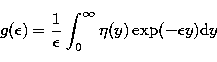 |
(59) |
with y=1/kT and
| 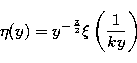 |
(60) |
(all the multiplicative constants have been put equal to one).
A linear inverse problem with discrete data
| 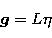 |
(61) |
can also be written in this case, with L defined by
| 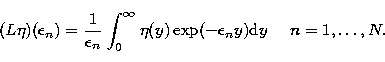 |
(62) |
If we introduce the 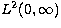 functions
functions
| 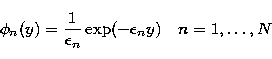 |
(63) |
the Gram matrix in this case is given by
|  |
(64) |
for  .
.
In Table 3 we compare the condition numbers for N=10, 25, 50, 100
geometrically sampled points (the energy range is again
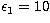 Kev,
Kev, 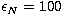 keV) for the thermal case and
the non-thermal models (thin- and thick-target) when the Kramers
cross-section is used (the Kramers' cross-section is the one adopted
to derive Eq. (57)). As one can see, the Laplace inversion problem
is much more unstable than the non-thermal problems.
keV) for the thermal case and
the non-thermal models (thin- and thick-target) when the Kramers
cross-section is used (the Kramers' cross-section is the one adopted
to derive Eq. (57)). As one can see, the Laplace inversion problem
is much more unstable than the non-thermal problems.
Table 3:
Condition numbers for the thin-target, thick-target and thermal models
when the Kramers cross-section is adopted, for different numbers N of
sampling points. The
photon energy range is 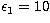 keV,
keV, 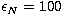 keV and the sampling
is geometric
keV and the sampling
is geometric
|
|


Up: Optimal inversion of hard
Copyright The European Southern Observatory (ESO)
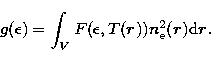
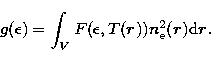


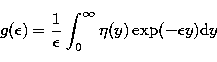
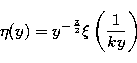
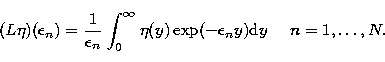
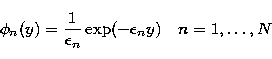

![]() Kev,
Kev, ![]() keV) for the thermal case and
the non-thermal models (thin- and thick-target) when the Kramers
cross-section is used (the Kramers' cross-section is the one adopted
to derive Eq. (57)). As one can see, the Laplace inversion problem
is much more unstable than the non-thermal problems.
keV) for the thermal case and
the non-thermal models (thin- and thick-target) when the Kramers
cross-section is used (the Kramers' cross-section is the one adopted
to derive Eq. (57)). As one can see, the Laplace inversion problem
is much more unstable than the non-thermal problems.