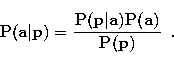
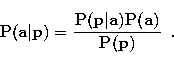 |
(2) |
The conditional probability ![]() describes the noise
in the data and its possible object dependence. It is fully specified in
the problem by the likelihood function. As indicated above, we have two
independent processes: image formation on the detector array and
detector readout. Taking the two processes into account, the
compound likelihood is (Núñez & Llacer 1993a):
describes the noise
in the data and its possible object dependence. It is fully specified in
the problem by the likelihood function. As indicated above, we have two
independent processes: image formation on the detector array and
detector readout. Taking the two processes into account, the
compound likelihood is (Núñez & Llacer 1993a):
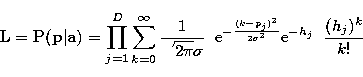
and its logarithm is:
![\begin{eqnarray}
\log {\bf L} & = & \sum_{j=1}^{D}{\left[-\log(\sqrt{2\pi}\sigma...
...ac{(k-p_j)^2}{2\sigma^2}}\;
\frac{(h_j)^k}{k!}\right)}\right]\;\;.\end{eqnarray}](/articles/aas/full/1998/13/ds6310/img29.gif) |
||
| (3) |
![\begin{displaymath}
\log {\bf L} = \sum_{j=1}^{D}{\left[- h_j +p_j\log h_j -\log
(p_j!)\right]}\;\;.\end{displaymath}](/articles/aas/full/1998/13/ds6310/img30.gif) |
(4) |
We use entropy to define the prior probability ![]() in a
generalization of the concepts originally described by Frieden (1972).
in a
generalization of the concepts originally described by Frieden (1972).
Let N be the total energy (usually the number of counts or photons) in
the object. Assume that there is an intensity increment ![]() describing an intensity jump to which we can assign some appropriate
physical meaning. Frieden (1972) describes
describing an intensity jump to which we can assign some appropriate
physical meaning. Frieden (1972) describes ![]() as the finest known
intensity jumps that are possible in the object, but we prefer to relax
that definition and consider it an adjustable hyperparameter of the
Bayesian function.
as the finest known
intensity jumps that are possible in the object, but we prefer to relax
that definition and consider it an adjustable hyperparameter of the
Bayesian function.
Assume, in addition, that we have prior information regarding the
statistical makeup of the object obtained, for example, from previous
observations or from observations at other wavelengths from which one
could infere realistic information about the makeup of the object at the
wavelength at which the observation is made. If ![]() is
the prior energy distribution, the prior probability of a photon going
to pixel i is given by:
is
the prior energy distribution, the prior probability of a photon going
to pixel i is given by:
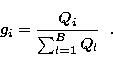
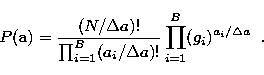 |
(5) |
If the prior information is not reliable, it is best to ignore it and
give a uniform value to ![]() that means
gi = 1/B. In that case, the multinomial distribution
of (5) reduces to a normalized version of the Boltzmann
distribution used by Frieden (1972).
that means
gi = 1/B. In that case, the multinomial distribution
of (5) reduces to a normalized version of the Boltzmann
distribution used by Frieden (1972).
Assume, also, that the intensity increment ![]() is space variant in
the object space. The introduction of the variability of
is space variant in
the object space. The introduction of the variability of ![]() is
the core of this paper. The parameter
is
the core of this paper. The parameter ![]() controls the amount of
prior information that is introduced into the solution. If the values of
Qi represent a uniform field, the parameter
controls the amount of
prior information that is introduced into the solution. If the values of
Qi represent a uniform field, the parameter ![]() will control
the degree of smoothness of the solution. Its spatial variability will
allow the local control of smoothness avoiding noise amplification in the
different areas of the image.
will control
the degree of smoothness of the solution. Its spatial variability will
allow the local control of smoothness avoiding noise amplification in the
different areas of the image.
Let ![]() be the variable increment. Now, in
place of
be the variable increment. Now, in
place of ![]() units we distribute
units we distribute ![]() units. The a priori source probability of
units. The a priori source probability of
![]() quanta distributing randomly
over the B pixels is then:
quanta distributing randomly
over the B pixels is then:
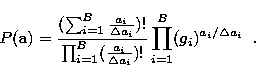 |
(6) |
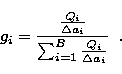 |
(7) |
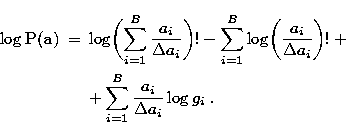 |
||
| |
(8) |
in which we discarded the term ![]() . This
approximation is adequate for x > 10. Also, the use of the complete
approximation would give a term in
. This
approximation is adequate for x > 10. Also, the use of the complete
approximation would give a term in ![]() in the algorithms that
would produce a numerical instability at the background pixels. In some
cases (p.e. in regions of very low flux or background in photon counting
devices) the approximation used may produce some error but we prefer to
use this approximation to avoid the menctioned numerical instability.
Using (10)
in the algorithms that
would produce a numerical instability at the background pixels. In some
cases (p.e. in regions of very low flux or background in photon counting
devices) the approximation used may produce some error but we prefer to
use this approximation to avoid the menctioned numerical instability.
Using (10)
![\begin{eqnarray}
\log {\bf P}({\bf a}) & = & \biggl( \sum_{i=1}^{B}{\frac {a_i}{...
...right]} + \\ & & + \sum_{i=1}^{B} \frac {a_i}{\Delta a_i} \log g_i\end{eqnarray}](/articles/aas/full/1998/13/ds6310/img48.gif) |
||
and taking into account (7) the logarithm of the probability ![]() is:
is:
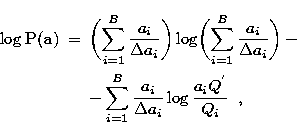 |
||
| (9) |
where
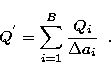
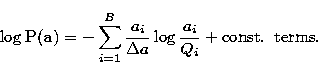 |
(10) |
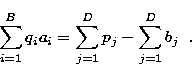 |
(11) |
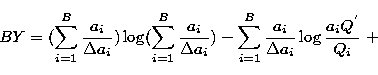
![\begin{displaymath}
+\sum_{j=1}^{D}{\left[-\log(\sqrt{2\pi}\sigma) - h_j +
\log\...
...{(k-p_j)^2}{2\sigma^2}}\;
\frac{(h_j)^k}{k!}\right)}\right]} - \end{displaymath}](/articles/aas/full/1998/13/ds6310/img60.gif)
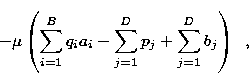 |
(12) |
where hj is given by:
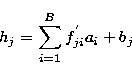
and ![]() is a Lagrange multiplier for the conserconservation of
counts. Note that the relative weight of the two terms in
the Bayesian function (17) is controlled by the set of
hyperparameters
is a Lagrange multiplier for the conserconservation of
counts. Note that the relative weight of the two terms in
the Bayesian function (17) is controlled by the set of
hyperparameters ![]() .
.
The nonlinear nature of the reconstruction problem described by (17) suggests an iterative algorithm. We have found that gradient methods, like steepest ascent or conjugate gradient algorithms, although well established, produce negative results for most of the pixels in the low light level part of the image. Also, the well-behaved Expectation Maximization (EM) algorithm -developed by Dempster et al. (1977) and extensively used for maximum likelihood reconstruction, after the work of Shepp & Vardi (1982)- is difficult to use in the Bayesian case with entropy because it requires the solution of transcendental equations in the M-step. Instead, we have found that the method of Successive Substitutions described by Hildebrand (1974) and Meinel (1986), and used by the authors in several previous papers, affords us greater flexibility than other methods and results in rapidly converging algorithms.
The Successive Substitutions method can be described as follows: given a
series of equations on the unknowns ![]() in the form
in the form
| |
(13) |
where F is some function, ![]() is the complete set of
variables
is the complete set of
variables ![]() , and K is a
normalization constant, (18) can be transformed into a recursive
relation by
, and K is a
normalization constant, (18) can be transformed into a recursive
relation by
| |
(14) |
Each of the new values of a(k+1)i is calculated from all the
known B values of ![]() , and the complete set is updated at once. The
constant K is obtained by invoking the energy conservation law:
, and the complete set is updated at once. The
constant K is obtained by invoking the energy conservation law:
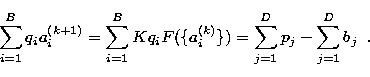 |
(15) |
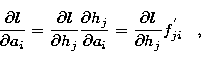
![\begin{eqnarray}
\frac{\partial BY}{\partial a_i} & = & -\frac{1}{\Delta a_i} \l...
...\frac{k(h_j)^{k-1}}{k!}f^{'}_{ji} \right)} \right] -\mu q_i = 0\;.\end{eqnarray}](/articles/aas/full/1998/13/ds6310/img73.gif) |
||
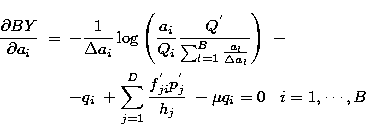 |
||
| (16) |
where
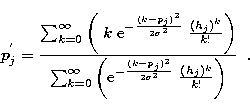 |
(17) |
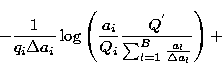
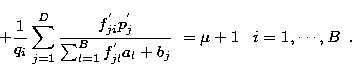 |
(18) |
![\begin{eqnarray}
a_i\left[\mu+1+C\right]^{n} & = & a_i\left[
\frac{1}{q_i}\sum_{...
...\Delta a_l}}}\right)
+ C\right]^{n} \nonumber \\ & & i=1,\cdots,B.\end{eqnarray}](/articles/aas/full/1998/13/ds6310/img78.gif) |
||
| (19) |
![\begin{eqnarray}
a^{(k+1)}_i & = & K a^{(k)}_i\left[
\frac{1}{q_i}\sum_{j=1}^{D}...
...lta a_l}}}
\right) + C\right]^{n} \nonumber \\
& & i=1,\cdots,B.\end{eqnarray}](/articles/aas/full/1998/13/ds6310/img79.gif) |
||
| (20) |
![\begin{eqnarray}
a^{(k+1)}_i & = & K a^{(k)}_i\left[
\frac{1}{q_i}\sum_{j=1}^{D}...
...log \frac{a^{(k)}_i}{Q_i} + 1
\right) + C\right]^{n} i=1,\cdots B.\end{eqnarray}](/articles/aas/full/1998/13/ds6310/img81.gif) |
||
| (21) |
![\begin{displaymath}
K = \frac{1}{\left[\mu+1+C\right]^{n}} \;\;\;,\end{displaymath}](/articles/aas/full/1998/13/ds6310/img83.gif)
The iterative process defined by (26), (23) is the
main result of this paper. We call this algorithm FMAPE. The algorithm
has a number of desirable characteristics: It solves the cases of both
pure Poisson data and Poisson data with Gaussian readout noise. The
algorithm allows us to adjust the hyperparameters ![]() in order
to determine the degree of smoothing in different regions or, in
connection with known default images, to adjust the proximity between the
reconstruction and the default image
in order
to determine the degree of smoothing in different regions or, in
connection with known default images, to adjust the proximity between the
reconstruction and the default image ![]() . The algorithm maintains
the positivity of the solution; it includes flatfield corrections; it
removes background and can be accelerated to be faster than the
Richardson-Lucy algorithm (Lucy 1974). The main loop (projection and
backprojection) of the algorithm is similar in nature to the Expectation
Maximization algorithm. The algorithm can be applied to a large number
of imaging situations, including CCD and Pulse-counting cameras both in
the presence and in the absence of background.
. The algorithm maintains
the positivity of the solution; it includes flatfield corrections; it
removes background and can be accelerated to be faster than the
Richardson-Lucy algorithm (Lucy 1974). The main loop (projection and
backprojection) of the algorithm is similar in nature to the Expectation
Maximization algorithm. The algorithm can be applied to a large number
of imaging situations, including CCD and Pulse-counting cameras both in
the presence and in the absence of background.
The algorithm contains two arbitrary constants n and C. Both have
been introduced in a way that the effect of changing the values of the
constants n and C only affects the calculated values of K at the
end of each iteration. The point of convergence of the
algorithm (26), (23) is then solely dependent on the
hyperparameters ![]() . This can be seen as follows:
Eq. (25) represents a set of B simultaneous equations in
the unknowns ai. Once the problem is solved by some appropriate
method, Eq. (25) will hold, independently of the values of
C and n. Equation (26) provides a method of solving the set
of Eq. (25). If it converges to a solution
of (25), that solution will therefore be independent of the
values of C and n.
. This can be seen as follows:
Eq. (25) represents a set of B simultaneous equations in
the unknowns ai. Once the problem is solved by some appropriate
method, Eq. (25) will hold, independently of the values of
C and n. Equation (26) provides a method of solving the set
of Eq. (25). If it converges to a solution
of (25), that solution will therefore be independent of the
values of C and n.
The constant C is introduced to insure the positivity of the solution. The presence of the negative entropy term
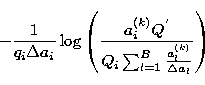
on the right hand of (26) means that the positivity of the solution is not automatically guaranteed unless an appropriate constant is introduced. As indicated above, different choices of C will not affect the convergence point. Such a problem is often present in maximum entropy approaches, either by gradient or EM algorithms.
Since the first term in (26) is always positive, a value of C somewhat larger than
![\begin{displaymath}
\max \left[ -\frac{1}{q_i \Delta a_i} \log \left( \frac{a^{(...
...ac {a^{(k)}_l}{\Delta a_l}}}
\right) \right] \;\;\;i=1,\cdots,B\end{displaymath}](/articles/aas/full/1998/13/ds6310/img85.gif)
will suffice. In practice, we find that changing C can affect the speed of convergence. Increasing C by a factor of 2 over the approximate smallest value necessary to maintain non-negativity results in slowing down convergence by approximately the same factor. The use of C=1 has usually resulted in adequate convergence speed and non-negativity of the pixels.
The constant n affects the rate of convergence. Since n affects the
correction factor in (26), one can expect a range of values of
n over which the iterative process is stable. We have observed that for
n=1, the convergence rate improves by a factor of approximately n with
respect to the rate for n=1. At the beginning of the process, when the
correcting factors are rather high, a large n could result in an
instability of the algorithm. After several iterations, when the
correcting factors are close to unity, large values of n can be used.
We have obtained stability using up to ![]() at the beginning of
the iterative process and larger values later.
at the beginning of
the iterative process and larger values later.
In the absence of readout noise or when it is negligible, ![]() in (23). Then the exponentials are dominant at
k=pj and
in (23). Then the exponentials are dominant at
k=pj and ![]() . We note that by its definition,
. We note that by its definition,
![]() is always positive, while the original data
is always positive, while the original data
![]() can be negative. For example, if the background is
small, as in the case of the Hubble Space Telescope, the mean background
is just above zero, but due to the readout noise, we may find a large
number of pixels with negative values. Negative values are not allowed in
any algorithm with projection-backprojection operations, like in the
classical Richardson-Lucy algorithm. A preprocessing of the data or other
approximations are common. We do not need any approximation or
preprocessing. In fact,
can be negative. For example, if the background is
small, as in the case of the Hubble Space Telescope, the mean background
is just above zero, but due to the readout noise, we may find a large
number of pixels with negative values. Negative values are not allowed in
any algorithm with projection-backprojection operations, like in the
classical Richardson-Lucy algorithm. A preprocessing of the data or other
approximations are common. We do not need any approximation or
preprocessing. In fact, ![]() is a representation of
the data that is positive and close to the data, with a degree of
closeness that depends on the projections
is a representation of
the data that is positive and close to the data, with a degree of
closeness that depends on the projections ![]() and
and
![]() . In this sense
. In this sense ![]() can be considered as a
Bayesian filtered version of the data.
can be considered as a
Bayesian filtered version of the data.
The practical computation of ![]() by
Eq. (23) is not a trivial problem of numerical analysis.
The p'js are numbers in the same range of the data, but to compute
them, we need to compute summations from to
by
Eq. (23) is not a trivial problem of numerical analysis.
The p'js are numbers in the same range of the data, but to compute
them, we need to compute summations from to ![]() . In addition,
exponentials and factorials can easily give either machine overflow or
underflow, even using quadruple precision. To solve the
problem Snyder et al. (1993b) use Poisson and saddlepoint approximations. We preferred to
use a recursive technique without any approximation with very good
results. Also, it is easy to see that the summations from k=0 to
. In addition,
exponentials and factorials can easily give either machine overflow or
underflow, even using quadruple precision. To solve the
problem Snyder et al. (1993b) use Poisson and saddlepoint approximations. We preferred to
use a recursive technique without any approximation with very good
results. Also, it is easy to see that the summations from k=0 to
![]() can be reduced to summations from
can be reduced to summations from ![]() to
to
![]() with
with ![]() without loss of precision. By using
this method, we can compute the p'j values with high accuracy,
without increasing the CPU time apreciably.
without loss of precision. By using
this method, we can compute the p'j values with high accuracy,
without increasing the CPU time apreciably.
We can obtain a maximum likelihood algorithm from the general FMAPE by
taking the limit when ![]() .In that case the weight of the prior information (cross-entropy term) in
the Bayesian function (17) is zero and the solution becomes a
Maximum Likelihood one. The algorithm for the maximum likelihood (MLE)
case in the presence of readout noise and background is:
.In that case the weight of the prior information (cross-entropy term) in
the Bayesian function (17) is zero and the solution becomes a
Maximum Likelihood one. The algorithm for the maximum likelihood (MLE)
case in the presence of readout noise and background is:
![\begin{eqnarray}
a^{(k+1)}_i & = & K a^{(k)}_i\left[
\frac{1}{q_i}\sum_{j=1}^{D}...
...}a^{(k)}_l}
+ C_jb_j}}\;\right]^{n} \nonumber \\ & & i=1,\cdots,B,\end{eqnarray}](/articles/aas/full/1998/13/ds6310/img96.gif) |
||
| (22) |
where p'j is given by Eq. (23).
In the case of no background and no readout noise, algorithm (28) becomes:
![\begin{displaymath}
a^{(k+1)}_i = a^{(k)}_i\left[
\frac{1}{q_i}\sum_{j=1}^{D}{\f...
...\sum_{l=1}^{B}{f_{jl}a^{(k)}_l}
}}\;\right]^{n}\; i=1,\cdots,B.\end{displaymath}](/articles/aas/full/1998/13/ds6310/img97.gif) |
(23) |
For n=1 and disregarding the gain (flatfield) corrections (qi=1), (29) is identical to the Richardson-Lucy algorithm.
Copyright The European Southern Observatory (ESO)