2 Notation and imaging model

The notation used in this paper is the following:

D Number of detectors in the array
B Number of elements (pixels) in the
		  reconstruction
$p_j, j=1,\cdots D$ projection (measured) data
$a_i,i=1,\cdots B$ emission density in the image
		 (parameters to  be estimated)
fji Point  Spread  Function  (PSF)  or
		  probability  that  an emission in
		  pixel i in the source be detected at
		  detector  j
$b_j, j=1,\cdots D$ background in the data
$n_j, j=1,\cdots D$ readout noise in the data
$C_j, j=1,\cdots D$ detector gain corrections (flatfield)
 
$f^{'}_{ji} = \frac{f_{ji}}{C_j}$ corrected  PSF
 
$q_i = \sum_{j=1}^{D}{f^{'}_{ji}}$ total detection probability for an
		 emission from pixel i 
$h_j = \sum_{i=1}^{B}{f^{'}_{ji}a_i} + b_j$ forward projection or blurring
		       operation
Qi prior  distribution density or default
		 image (if any)

let ${\bf p,a,f,b,n,C,f^\prime,q,h,Q}$ be the corresponding arrays.

We shall work with the following imaging model: an object emits light with an intensity given by a spatial distribution ${\bf a}$. The light is focused by the optical system over a detector array consisting of individual, discrete, independent detectors. Each detector has a different quantum efficiency characterized by a gain correction distribution ${\bf C}$. A certain background radiation ${\bf b}$,coming mainly from the sky but also from sources inside the detector system, is detected along with the spatial distribution ${\bf a}$. We assume that the detection process is Poisson distributed. Finally, the detector is read by an electronic process which adds a Gaussian readout noise ${\bf n}$ with zero mean and known standard deviation $\sigma$. The imaging equation corresponding to this model is:

 

$${\bf f^{'}\;a + b + n = p}\;\;.$$ (1)

Equation (1) in discrete form becomes:

$$\sum_{i=1}^{B}{\frac{f_{ji}}{C_j}\;a_i} + b_j + n_j = p_j \;\;\;\;j=1,\cdots,D\;\;.$$

Most imaging systems are described by Eq. (1), particularly those based on Charge Coupled Device (CCD) cameras, and Image Pulse Counting Systems (IPCS).

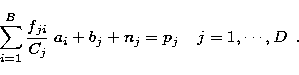
The background in Eq. (1) is an input in our algorithm. Some authors (Bontekoe et al. 1994; Narayan & Nityananda 1986) have raised questions about the introduction of the background in Eq. (1). Bontekoe et al. demonstrated that the solution depends on the background in standard Maximum Entropy Method (MEM) algorithm. However, in our approach, the background term includes not only light from the sky but also light from sources inside the camera. In the case of a CCD camera, the background term b can be considered as: ${\bf b} = {\bf b}_{\rm ext}+ {\bf b}_{\rm int}+ {\bf b}_{\rm dark}+ {\bf b}_{\rm bias}$ (Snyder et al. 1993). The term ${\bf b}_{\rm ext}$ is the external background radiation. The term ${\bf b}_{\rm int}$ is the internal background radiation from luminiscent radiation on the CCD chip itself. The term ${\bf b}_{\rm dark}$ is the number of thermoelectrons that are generated by heat in the CCD and ${\bf b}_{\rm bias}$ is the number of electrons that are due to bias or "fat zeros". Those terms are all Poisson distributed random variables and their sum can be represented by a single background term. We have not observed in our algorithm the background dependence effect reported by Bontekoe et al. (1994). In our opinion, if the background is large and acurately known, it is better to include it in the equation and in the reconstruction algorithm. Otherwise, it is always possible to set it to zero in the algorithm and reconstruct the background as part of the image.