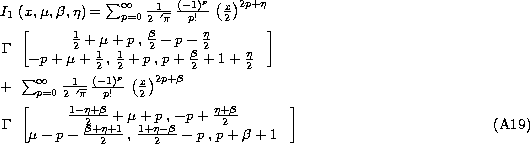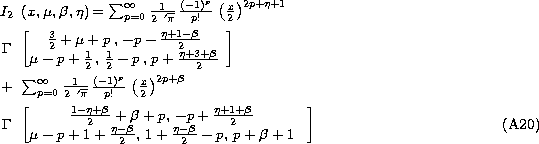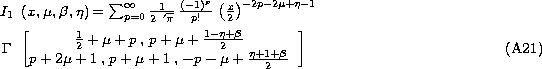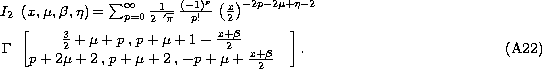As demonstrated by Sasiela (Sasiela 1994), the properties of Mellin transforms
(see for instance (Colombo 1959;
Dautray & Lions 1987)) and Gamma functions
are useful in problems dealing with wave propagation in turbulence. This
technique is applied here to solve the integral in Eq. (12 (click here)),
Eq. (24 (click here)), Eq. (34 (click here)) and Eq. (35 (click here)).
The Mellin transform pair is given by:
The general form of the integral to solve has been presented by Chassat
(Chassat 1989) and can be written (
):
From the properties of the Mellin transforms
(Colombo 1959; Dautray & Lions
1987) and using 
, the
integral becomes:
Tables of Mellin transforms
(Sasiela 1994; Colombo 1959;
Dautray & Lions
1987) are helpful to solve Eq. (A3 (click here)). Moreover, the Mellin transform
of functions can usually be expressed as the ratio of Gamma functions. We use
the notation:
We have for Jn the 
order Bessel function of the first
kind:
It leads to the Mellin-Barnes integral:
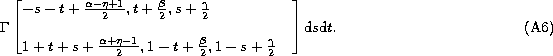
This integration can be performed using the method of pole residues. The value
of the integral, as given by Cauchy's formula, is just 2i
times the sum
of the residues at the enclosed poles. The result can be expressed in terms of
generalised hypergeometric functions
(Abramovitz & Stegun 1965). For instance,
in the case 
1, one of the interesting cases, the
integral is given by:
where:
When the function is expressed in terms of generalised hypergeometric functions,
the integral leads to the more restrictive convergence condition which
can be expressed as: 
. This condition determines
the maximum field of view which can be reached by this method.
The limited convergence domain encountered in the evaluation of integrals
involving the product of three Bessel functions has been first remarked by
Tyler (Tyler 1990). Chassat proposed a method using the Bessel recurrency
law (Chassat 1992):
Two easily evaluable Mellin integrals appear, 
and
With the notation 
and 
, Eq. (A2 (click here)) becomes:
The Bessel reccurency law becomes reccurency law between Mellin integrals which
can be written as:
Now, we can use the Mellin transform tables to solve 
and
which can be expressed as Mellin-Barnes integrals of the
following type:
where G and F are the Mellin transform of g and f
respectively. g and f are
defined as:
We have the Mellin transforms:
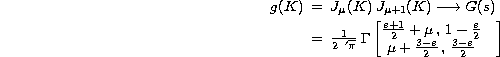
The Mellin transform of f(Kx) is given by Eq. (A2 (click here)).
Finally, using the Cauchy's formula, we find:
