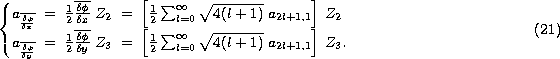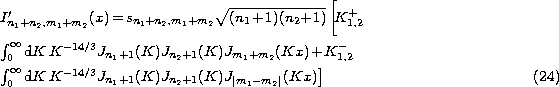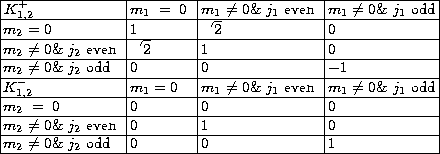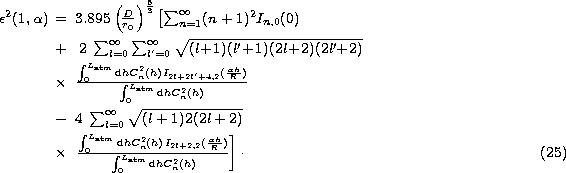In the previous paper
(Molodij et al. 1996), we have presented a new tracking
method, called granulation tracking, for measuring image motions by which
extensive sources can control a tiltable mirror in real-time. The principle
of this method is to monitor the variation of the image Fourier transform with
respect to some reference, in order to estimate its motions. The image is
detected by two detectors (Reticon 128 s photo-diode arrays), which
cover a
square field together but which each have resolution in one direction only.
The reticon has elongated
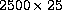micron pixels that are sensitive to motion
in the direction of the smaller diode dimension. Therefore, in the granulation
image, the cross-section of the two arrays defines a square field of view
which can be adjusted from 
arcsecond to 
arcsecond, depending on the
Fried parameter r0 (Rayrole 1992).
This tracking method, as in correlation tracking method, uses extended solar
granulation images as target structure to detect wavefront aberrations. The
size of the analyzed field of view is adjusted so the tracker will successfully
operate under any seeing conditions. One has to keep in mind, however, that
wavefront slope measurements are made to correct pure wavefront tilts.
All higher order aberrations such as coma Zernike polynomials (Z7 or Z8)
are interpreted by the system as image motions because it is not possible to
distinguish between, for example, a tilt in the wavefront and deformations of
the object itself. The granulation tracker can not determine the appropriate
tilts of the wavefront surface (which is the best correction in term of Strehl
resolution). Such wavefront analyzer system determine relative displacements
of successive images in real time. These shifts constitute arbitrary position
of stabilization defined both by the target motions and the target structure
deformations, which are applied to the tilting mirror.
We propose to analyze the problem of the wavefront slope measurement
calculating the first phase derivative expansion on the Zernike polynomials
using Primot's approach (Primot et al. 1990) in order to determine the image
quality after image stabilization from wavefront slope measurements.
The wavefront slope measurements (in x and y direction) can be written:
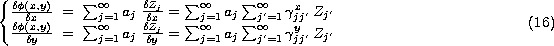
where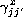 
and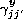 
are the matrices expressed by Noll
(Noll 1976) for representing derivatives of Zernike polynomials as a linear
combination of Zernike polynomials.
We can express the wavefront slope measurements over the circular aperture of
the telescope. For instance, the wavefront slope in x direction, denoted
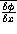is written:
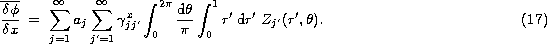
Let us notice that averaging the Zernike polynomials over the aperture of the
telescope is zero if j' > 1:
So that:
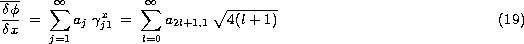
where the notation Zj(n=2l+1,m=1) is adopted to define the concerned Zernike
polynomials (the radial degree is odd and the azimutal frequency m = 1 because
the averaging over the circular aperture). The measured quantity is quite
different from pure tilt Zernike polynomials. Wavefront tilt Z2 not only
appear to define the first mean phase derivative in x direction, but also
the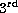 
order coma Z8 and higher order aberrations such Z16,
Z30, Z46, Z68 etc.. Wavefront tilt Z3 and others Zernike
polynomial aberrations as Z7, Z17, Z29, Z47, Z69 etc.
appear to define the first mean phase derivative in y direction.
Therefore, the estimated wavefront reconstructed by the system from the
measurements can be written:
with:
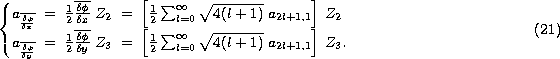
Figure 1: Angular correlation functions for the higher order
aberrations participating in the modal expansion of the first
phase derivative
versus the angular separation. The notation Zj(n=2l+1,m=1) is adopted to
define the concerned Zernike polynomials j (n is the radial
degree and m the azimuthal frequency). These correlations are calculated
using the simulated Cn2 turbulence profile (D/r0= 5)
from experimental
measurements at Iza
a site by Arcetri University
(Barletti et al.
1973)
Let us remark that effects of anisoplanatism must be taken into account to
understand all the effects that might arise when adjusting the analyzed field
of view of the target from arcsecond to arcsecond. The statistical
analysis of angular cross-correlation allows to determine the aberration
strenghts of all the higher order aberrations participating in the modal
expansion of the first phase derivative of Eq. (21 (click here))
in such situation.
Figure 1 (click here) shows the normalised angular correlation functions of
the first polynomials of the expansion concerned for the 0.9 m telescope
diameter (T.H.E.M.I.S.). These correlations are calculated using the simulated
Cn2 turbulence profile (Fig. 2 (click here)) from experimental
measurements at Izaa site by Arcetri University
(Barletti et al.
1973). For a given angular separation 
corresponding to the size of the
field of view analyzed by the granulation tracker, the only Zernike polynomials
defined by Eq. (21 (click here)) which are useful in the measured quantity, are the
polynomials having their 50% correlation angle larger than .
The peculiar shape of the curves is related to the turbulence
profile simulated, (r0 = 18 cm of Fig. 2 (click here))
(Barletti
et al. 1973).
The higher order aberrations participating in the modal expansion of the
first phase derivative of Eq. (21 (click here)) are correlated on the field of view
delimitated by the granulation tracker so that the measured quantity by the
analyzer is very close to the wavefront slope.
Figure 2: Cn2 turbulence profile from experimental
measurements at Izaa site by Arcetri University
(Barletti et al.
1973). The profiles are integrated from 10 m (above the ground) to 2000 m
to give Fried's parameter r0 at 
= 0.5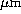 
from 10 cm to 22
cm (respectively D/r0 from 9 to 4)
Let us notice that Fig. 1 (click here) reveals the strong dependence of the
angular correlations on the angular separation and the
radial degree
n. If the decorrelation of the tilts (n=1) is slow when increasing ,
for others polynomials the decorrelation is steep. This result is general in
the modal analysis of the effects of the atmospheric turbulence on the
wavefronts (Rousset 1993).
Let us now consider how the correction is made by the image stabilizer system
considering the residual wavefront error Eq. (7 (click here)) when correcting
pure wavefront tilts from slope measurements.
The estimated wavefront tilts by the system are given by Eq. (21 (click here))
so that the residual error becomes:
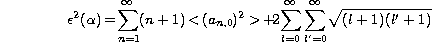
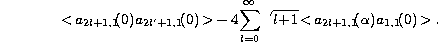
The residual error after image stabilisation expansion contains angular
cross-correlation of Zernike polynomials j1(n1,m1) and j2(n2,m2):
<an1,m1 an2,m2> which can be calculated introducing minor
corrections in Eq. (11 (click here)):
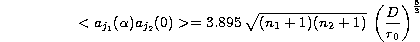
where In1+n2,m1+m2'(x) is now written:
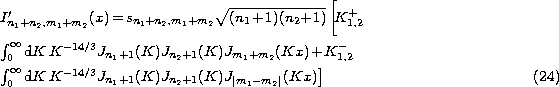
where K1,2+ and K1,2- ,quantities depending on the coefficient
pairs (j1,j2) parity, are listed in Table 1 (click here).
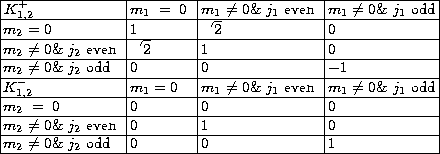
Table 1: Angular cross-correlation
Zernike polynomial coefficients
The residual wavefront error
after image stabilization may be expressed:
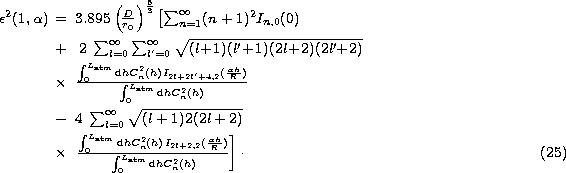
In any case the residual phase variance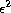 
can be estimated from the
knowledge of the Zernike coefficient angular correlations.