In order to determine the compensation quality in a field of view, the residual
phase variance over the telescope aperture is expressed expanding the turbulent
wavefront on the Zernike polynomials (or modes). The properties of Zernike
polynomials, denoted Zj, are well described by Noll
(Noll 1976) whose
notation is adopted.
The wavefront 
incoming from a determined area on the
Sun, located at angular distance 
from the on-axis observed direction, is
expanded as (piston mode removed):
where 
is the normalized position vector in the aperture, R the
radius of the telescope aperture and the 
the Zernike expansion
coefficients given by:
introducing the Noll normalisation function:
So, the polynomials 
normalised on the telescope aperture
are defined in polar coordinates 
by:
and
where n is the radial degree of the 
polynomial and m its azimuthal
frequency.
Let 
be the estimated wavefront reconstructed by
the adaptive optics system on the first J polynomials from the measurements.
In this paper, noise in the wavefront measurement will not be considered,
therefore we write:
The residual phase variance 
is estimated for an adaptive
optics system having J degrees of freedom and for an angular distance
between the two directions, calculating:
Using the orthogonality properties of Zernike polynomials, Eq. (1 (click here))
and Eq. (6 (click here)), and the stationarity hypothesis, the residual phase
variance is:
This result is classical in the estimation of wavefront residual error on the
Zernike polynomial (Chassat 1989; Rousset 1993).
The first term in brackets of the right hand side of Eq. (8 (click here)) represents
the fitting error for an adaptive optics system which corrects the first J
polynomials. It has been given by Noll (Noll 1976). The other term of the
right hand side of the Eq. (8 (click here)) is the spatial and angular wavefront
errors.
The residual error can be written as:
The quantity 
) is the spatial and angular error for the corrected
polynomial Zj. Correction by the adaptive optics system will be effective
when 
is larger than 0 for each polynomial Zj, i.e. when:
When the criterion of Eq. (10 (click here)) is satisfied, the measured wavefront
at angular distance provides a satisfactory fit of the on-axis
wavefront when the correlation criterion of Eq. (10 (click here)) is verified for
all the correction modes. For instance, this criterion allows to select the
number of useful correction modes for a given angular distance between the
two wavefronts. Keeping in mind that all the low orders must be first corrected,
a higher order mode will be corrected only if the criterion is verified.
This result is general in wavefront residual error estimation for adaptive
optics using the modal analysis (Rousset 1993).
Now, the Zernike coefficient angular correlations
between the two wavefront directions can be derived as indicated in References
(Valley & Wandzura 1979; Chassat 1989;
Molodij & Rousset 1997).
Therefore, the Zernike coefficient angular correlation can be written as:
where r0 in this equation is the Fried parameter, D is the telescope
diameter (D=2R), Cn2 is the turbulence profile, h is the altitude along
the propagation path from 
(the effective altitude of the considered
atmosphere is 20000 meter) to the telescope, and using the notation
:
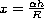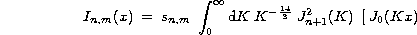
where K is the Fourier space of the Zernike polynomials in polar coordinates
(Noll 1976).
and
Let us notice that it is also possible to deduce from Eq. (11 (click here)) and
(12 (click here)), the Zernike polynomial coefficient variances. The result is in
perfect agreement with the variances given by Noll
(Noll 1976). Let us remark that the variance only depends on the radial degree n and is given by:
where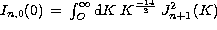 
.
To calculate the residual phase variance Eq. (8 (click here)), we consider first
that the number J of corrected polynomials is chosen in order to include all
the polynomials of the maximum radial degree N. Knowing that there is n+1
polynomials per radial degree n, we have therefore:
.
Secondly, the azimuthal frequency symmetry properties of Zernike coefficient
correlations are useful. Summation on all azimuthal frequencies of a radial
degree leads to only a radial degree dependence. Then, we have using
Eq. (11 (click here)):
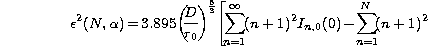
Integral In,m(x) (Eq. (12 (click here))) can be evaluated in closed form using Mellin transform techniques as proposed by Sasiela and expressed in terms of rapidly converging series (Sasiela 1994). This integral is transformed into a Mellin-Barnes integral and is then expressed as a sum of generalised hypergeometric functions in the appendix A. As mentioned by Tyler (Tyler 1990), this analytic form is related to integral involving product of three Bessel functions and can be evaluated only for restrictive cases, i.e. here depending on the angular separation. To overcome this limitation, Chassat (Chassat 1992) proposed an analytic solution applying a recursive development which is also presented in the Appendix.