The image quality obtained, after the T.H.E.M.I.S. adaptive optics system is applied,
can be evaluated by comparing the restaured image frequencies of the optical
tranfer function in the field of view. The optical transfer function after
correction (OTF) can be defined as the mathematical expectation of the
cross-correlation function of the complex amplitude 
of the
compensated wavefront.
Assuming that scintillating effects are negligible, this amplitude can be
written:
where the wavefront after compensation 
is the difference
between the wavefront 
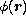coming from the observed source
and the estimated wavefront 
reconstructed by the
adaptive optics system from the measurement at angular distance 
.
Assuming the near field approximation is verified, the OTF can be written:
where 
is the normalised function defined by Eq. (3 (click here)).
Having remarked that phase is a Gaussian random function
(Roddier 1981),
Eq. (30 (click here)) becomes:
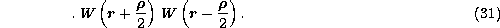
The statistics of the Zernike coefficients for an expansion of Kolmogorov
turbulence phase distortion have been applied by Wang and Markey to calculate
the OTF for a point source case ( = 0)
(Wang & Markey 1978).
We have extended the method to cases when the observing source is extended
in order to evaluate the degradation in the field of view of the image due to
anisoplanatism after adaptive optics compensation.
Using Eqs. (1 (click here)) and (6 (click here)) for the wavefront expansions, the argument
of the exponential of Eq. (31 (click here)) can be expressed as:
We recognize in the right half of the equation the first term as the wave
structure function. For a Kolmogorov type of turbulence, the wave structure
function for a plane wave can be expressed:
The cross-correlations of the Zernike coefficients 
are
calculated when the reference source target is at angular distance
from the observed source for J corrected modes by the adaptive optics system
(see Appendix). The turbulence profiles Cn2 used in the calculation of the
angular cross-correlation are presented in Fig. 2 (click here):
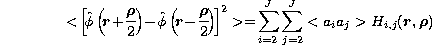
Introducing the notation:
The OTF in the field of view is obtained evaluating the following numerical
expression as indicated by Wang & Markey
(Wang & Markey 1978):
with
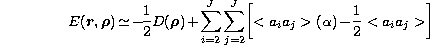
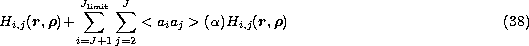
and
where 
is the argument of 
.
First, we have verified that the infinite sum can be stopped at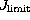 
=
91 when the compensating phase distribution is an expansion through coma
J = 10 and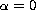 
, as indicated by Wang and Markey.
Secondly, when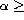 
10 arcsec with the considered turbulence profile,
the cross-correlation terms can be approximated by truncating the infinite
sum over a more appropriate limit around 
(for an estimated
convergence at 10-8). This is due to the fact that the loss of
cross-correlations of higher order aberrations is more important in the field
of view (depending on ) than the lower orders.
Figure 6: 
versus the normalised spatial
frequency (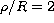
corresponds to the diffraction limited, i.e. a
spatial resolution around 0.145 arcsec
at 
), for
several orders of modal corrections
(compensation through coma J = 10,
compensation of tilts J = 3 and after
image stabilization), at D/r0 = 5.
The full curve is the diffraction
limited comparatively to the dot curve
without correction
Figure 6 (click here) shows the OTF(=0) versus the spatial
frequency calculated with the turbulence profile presented
in Fig. 2 (click here)
and zero field of view
for 10 orders of correction (compensation
through coma) and for 3 orders of correction
(compensation of tilts) comparatively
to image motion correction (image stabilization).
The results obtained for J = 10 and J = 3 agree exactely with the analytical
calculation reported by Wang
and Markey.
Figure 7: OTF(=0) versus the normalised spatial
frequency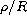 
, for various level of turbulence taking into account the
central obscuration of telescope T.H.E.M.I.S. (u = d / D = 0.44).
The Cn2
turbulence profiles used in the calculations, have been simulated from
experimental measurements made at Iza
a site. The full curve is the
diffraction limited
An analytic expression of the OTF taking into account the central obscuration
of the telescope has been published by Perrier
(Perrier 1989). Therefore, the
OTF can be written:
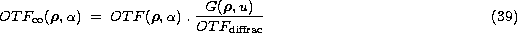
where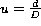 
is the linear central obscuration by comparison to the
T.H.E.M.I.S. diameter D. In this case u = 0.44.
Figure 7 (click here) presents the image quality improvement after compensation
by the image stabilizer system taking into account the central obscuration of
the magnetograph for various levels of turbulence and zero field of view. One
observes that the image quality improvement grows
when the turbulence strength expressed by Fried's
parameter r0 increases, i.e.,
when the ratio D/r0 decreases. For instance,
in Fig. 7 (click here) the
image motion stabilization is insufficient
for high turbulence levels caracterized
by a ratio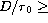 
6 when imaging in the visible wavelength
(). High spatial frequencies are
not restored by image stabilizer
system compensation.
Effects of anisoplanatism are presented in Fig. 8 (click here).
The OTF for compensation through the coma J = 10 are shown for different angular
separations in the field of view for the same turbulence profile. As expected
comparing with Fig. 4 (click here), one observes that the image quality
improvement when compensating 10 modes decreases rapidly when the angular
separation increases for an extended source. At very large angle (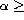
20 arcsec) in Fig. 8 (click here), the image quality after compensation of
10 modes for
D/r0 = 5 is hardly better than the one obtained without
correction, because of the wavefront angular decorrelation.
Figure 8: OTF() versus the normalised spatial
frequency 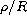, for several angular separation for a
compensation by the adaptive optics system through the coma J=10. The full
curve is the diffraction limited
Figure 9: Relative OTF = OTFJ=10 / OTFJ=3
versus the normalised spatial frequency 
for several angular
separations in the field of view. Curves are calculated with the
modelised profile (r0 = 18 cm from experimental measurements at
Izaa site by Arcetri University
(Barletti et al. 1973)
In Fig. 9 (click here) the relative OTF corresponding to the ratio of
the OTF after compensation through J=10 by the OTF
after compensation through
J=3, OTF = OTFJ=10 / OTFJ=3, are plotted versus the normalised spatial
frequency for different angular separations . Figure 9 (click here)
allows to understand the problem of the degradation of the compensation in the
field of view due to anisoplanatism when increasing the order of correction from
J = 3 up to J = 10. In the case of point source correction (curve
= 0), increasing the order of correction permits a higher-level image quality.
In the case of an extended source (
arcsec for the turbulence
profile studied), increasing the order of correction can be detrimental to the
image quality. For instance, the curve 
arcsec of Fig. 9 (click here)
shows that higher spatial frequencies 
are degraded when
the compensating phase distribution is an expansion through coma comparatively
to a tilts compensation by the adaptive optics system. This anisoplanatism
effect can be understood by remarking that the loss of correlation is faster
for the higher order coefficients than for low order. Of course, this behaviour
is emphasized in the comparison between OTFJ=10 and OTFJ=3 because
of the large isoplanatic patch for the tilt aberration. Similar conclusions
were found by Abitbolt and Ben-Yosef
(Abitbolt & Ben-Yosef 1991).
We present the results of numerical simulations to analyze the effects of
anisoplanatism when observing extended sources with possible configurations of
adaptive optics system which could be considered for practical implementation
on T.H.E.M.I.S. We compute analytically the long exposure optical tranfer functions
OTF in the field of view (for different angular separation ) in order
to simulate the filtering process of the atmospheric turbulence on the spatial
frequencies of a long exposure image of the solar granulation.
Figure 10 (click here) demonstrates the necessity to use adaptive optics
system to compensate the terrestrial atmospheric perturbations on wavefronts
coming from the Sun to the telescope (comparison between Fig. 10 (click here)a
and Fig. 10 (click here)b). Figure 10 (click here)a shows a 15 arcsec2
field of view of the solar granulation obtained with short exposures
(
few ms in imagery mode). This image allows to simulate the effects of
atmospheric turbulence in cases when long exposure are indispensable for
accurate measurements in spectroscopy mode ( 300 ms) before and after compensation.
A comparison of the effects of anisoplanatism is shown on an extended image
of solar granulation after real time compensation by the image stabilizer
system and by a 10 controlable modes adaptive optics system (Fig. 10 (click here)c and
Fig. 10 (click here)a).
Let us underline the significant improvement of the image quality when
compensating the 10 first aberration modes on this small field of view of the
image granulation (Fig. 10 (click here)d). By comparison, the on-axis correction
is relatively good with the image stabilizer optical system. It reveals the
importance of the contribution of the tilts in the adaptive optics compensation
when observing with a 90 cm telescope aperture for mean atmospheric turbulences.
Notice also that tilt variances represent 90% of the total variance phase
(Noll 1976).
Figure 11 (click here) presents the same comparison on a very large field
of view (around 50 arcsec2). One observes the significant increase of
anisoplanatism effects in the field of view with the increase of the number of
corrected modes (Fig. 11 (click here)c: image stabilization with a tip-tilt
mirror, Fig. 11 (click here)d: compensation through the coma J = 10). This
simulation allows to understand that for small field of view observations,
compensation of the 10 first aberration modes is the best choice in terms of
image quality keeping in mind the fast degradation of this quality in the field
of view as shown by Fig. 11 (click here)d. In contrary, with image stabilization,
the image quality does not vary fastly with the field angle. It reveals the
important contribution of the large isoplanatic patch of the tilt aberrations
for the adaptive optics compensation. At very large angle (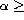 20
arcsec),
the correction with the image stabilizer optical system (Fig. 11 (click here)c)
is even better than the one obtained with the compensation of 10 first aberration
modes by adaptive optics system (Fig. 11 (click here)d).
Figure 12 (click here)a demonstrates the capacity of image stabilizer
system for large field of view observations and medium image quality. The
on-axis correction is relatively good considering the evaluation of the
Fried's resolution (0.45 arcsec in the center part of the field of view) and
the degradation does not vary fastly with the field angle. This is due to the
dominant contribution of the lawest altitude layers in the angular correlation
of the wavefronts. This system is well designed for solar observations like
sunspots (up to 30 arcsec), active regions and protuberances (few arcminutes).
Notice that the temporal analysis of solar phenomena needs also an homogeneous
field of view.
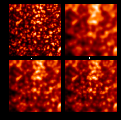
Figure 10: A) Solar granulation at diffraction
(short exposure). Image obtained by R. Muller. The size of the
field-of-view is 
arcsec. B)
Effects of the turbulence for long
exposure. The Fried's resolution is around 0.8 arcsec (r0 = 18 cm). The
turbulence profile has been simulated from experimental measurements at
Izaa site by Arcetri university
(Barletti et al. 1973). C)
Anisoplanatism effects after real-time compensation by the image stabilizer
optical system. D) Anisoplanatism effects after correction of 10 controlable
modes (tilt, focusing, astigmatism and coma)
Figure 11: A) Solar granulation at diffraction (short
exposure). Image obtained by R. Muller. The size of the field-of-view is
50x50 arcsec. B) Effects of the turbulence for long exposure. The
Fried's resolution is around 0.8 arcsec .
The turbulence
profile has been simulated from experimental measurements at Izaa
site by Arcetri university
(Barletti et al. 1973). C) Anisoplanatism effects
after real-time compensation by the image stabilizer optical system. D)
Anisoplanatism effects after correction of 10 controlable modes (tilt,
focusing, astigmatism and coma)
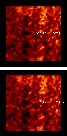
Figure 12: Evaluation of Fried resolution in the
field-of-view (50 arcsec) for image stabilizer system (top: A) and (bottom:
B) for adaptive optics system after correction of 10 controlable modes
(tilt, focusing, astigmatism and coma). By comparison, the resolution
without correction is only 0.8 arcsec
By comparison, Fig. 12 (click here)b allows to understand that for small field of view observations, the 10 corrected modes adaptive optics system is the best choice in terms of image quality keeping in mind the fast degradation of the quality in the field (resolution of 0.25 arcsec up to 0.62 arcsec in the 50 arcsec field). This demonstrates the importance of the decorrelation of the higher wavefront deformation modes in the field. So, the fast degradation of the resolution in the field will be problematic for many astronomical observations. Nevertheless, this system will be well designed to the observation of concentrated structures of the magnetic field (0.2 arcsec), penumbra fibrils (0.5 arcsec) or details of sunspots.