C. Calculations with B-splines

  Computation with B-spline is not familiar in stellar modelling, so I briefly describe the basic of the method directed towards interpolation and integration of differential equations. For more advanced description and proofs refers to deBoor (), Shumaker () and to the literature cited herein.

With this technique the functions to be interpolated (respt. integrated) e.g. pressure, temperature, etc... are approximated by piecewise polynomials which coincide with the function at interpolation points (respt. fulfill the differential equation). With a lattice with points at q_i, for algebra, the simplest way for writing piecewise polynomials at the location q, is the use of the canonical basis, i.e., the powers of (q-q_i). For the calculations that basis leads to algorithms having poor stability conditions; among the bases available for the linear set of piecewise polynomials, a local basis, the normalized B-spline basis, leads to stable algorithms.

A B-spline is itself, obviously, a piecewise polynomial. It can be defined either from divided differences (deBoor, loc. cit.; Gaches, 1988), or from the algorithm used for their calculation; they are convolution products of the (door) function (Marchouk & Agochkov 1985).

C.1. The nodal vector: the key of the computations with B-splines

  Before going ahead in the definition of the B-splines, one must define more precisely what is a piecewise polynomial of order s, on a given partition of [1,n], : is defined as a function which coincides, on each sub-interval , with a polynomial of degree s-1. The existence and uniqueness of on results from the knowledge, at each breakpoint q_i, of the kind of connection which is required between the right and the left pieces of polynomials. As an example, the so-called "natural spline" is a piecewise polynomial of order 4 (degree 3), constructed in such a way that, at the inner breakpoints , the second derivatives are continuous.

Formally, the rules of connection can differ from one breakpoint to the next: at some of them, can be discontinuous, at some others the left and right pieces can be tied fulfilling the continuity of their first derivatives or only of , etc...\ For each q_i, the connection is characterized by the so-called multiplicity m_i obtained as follows: let be the order of the oscularity of the connection between the left and right polynomial pieces at the breakpoint q_i; d_i=0 means continuity of , d_i=1 means continuity of the first derivative, d_i=2 () of the second ones etc... and one sets d_i=-1 for a discontinuity of the function itself. At i=1 and i=n (inner and outer boundaries) one fixes the value of . This is equivalent to assume that is discontinuous at these points. Hence, one has d₁=d_n=-1. The multiplicity of the point q_i is then defined as:

From the vector of multiplicities: one constructs the heart of the calculation with B-spline: the so-called "nodal vector": associated to a B-spline basis; it is the vector which has the q_i for coordinates, each of them appearing m_i times. is written:

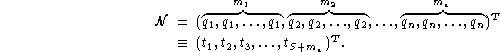
The dimension of is then S+m_n, with . A convenient schematic representation of a nodal vector consists in writing one column of m_i elements for each breakpoint q_i.

As an example, with s=4, n=7, continuity of at q₃, of at q₆, of at q₂ and q₅, and discontinuity of at q₄, the nodal vector is represented as:

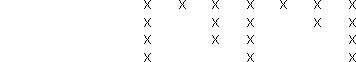
Once given this nodal vector, the value of the k-th normalized B-spline on () is obtained by induction:

and, for :

Note that its first derivative can easily be calculated:

From these relationships one can see that if . Hence the B-spline basis is a local basis. Moreover, , only s B-splines of order s are not identically zero and their sum is equal to 1. For their calculation, algorithms which avoid zero denominator have been designed. The present work uses the Schumaker's () algorithms 5-5, 5-11 and 5-13.

It can be shown that the set of all the B-splines , forms a basis for the linear space of the set of the piecewise polynomials having for nodal vector. Thus, the dimension of is precisely S.

For discontinuous piecewise polynomials the use of B-spline basis is particularly convenient since only the algorithm which constructs the nodal vector is concerned with the discontinuity.

The extension to several dimensions are found in Schumaker (loc. cit.) and in deBoor (loc. cit.)

C.2. Interpolation

  Let f(q) be a real function to be interpolated on the grid , ( if ), at each q_i, f(q_i) is known. For interpolation of order s the so-called Schoenberg's basis allows to reach an accuracy almost optimal (deBoor, loc. cit., Chapt. XIII, p. 219). The n coordinates of this nodal vector are written:

The dimension of this basis is exactly n. As an example, the standard natural spline of interpolation employed this basis, with s=4, the interpolating function is a cubic piecewise polynomial with pieces continuously connected up to second derivative.

C.3. Computation of the B-spline coefficients

  For the interpolating piecewise polynomial is written:

where the coefficients p_i fulfill the linear system:
 
It is a banded, totally positive linear system, thus it can be accurately solved by Gauss elimination without pivoting (deBoor, loc. cit., Chapt. XIII, p. 203).

C.4. Piecewise polynomial interpolation is conservative

  First briefly recall that standard polynomial interpolation is conservative. Let be a set of real functions to be interpolated on the grid , if . The polynomial P(x) for interpolation is written (Stoer & Bulirsch, ):

where L_j(x) is the j-th. Lagrange's polynomial. Owing to the property:

if any linear combination holds for the functions, e.g. conservation of baryon and charge numbers are relationships of that form, then:

it also holds for the polynomials of interpolation:

Piecewise polynomials have the same property, since between to break points (i) they are polynomials and (ii) according to the Schoenberg-Whitney theorem (deBoor, loc. cit., p. 200, Theorem XIII.1) where is at least a location where the linear combination is fulfilled. As seen Sect. 3.3.1 (click here), the chemicals are interpolated using piecewise polynomials, the former property ensures the conservation of baryon and charge numbers.

C.5. Integration of differential equations

  One seeks, on [a,b], the solution of a differential equation in the form of piecewise polynomials. Then, with respect to their B-spline basis, of order s, at q, for the variables, the piecewise polynomials are written:

where the p_k,j are the coordinates of the j-th unknown with respect to the B-spline basis. The quantities to be calculated consist in the B-spline coefficients p_k,j, rather than in the functions themselves. Formally, each of the differential equations can be expressed, for the p_k,j, in the form:
 
where the function is the jth. coordinate in the right hand side of the differential equation. Hence, derivatives of the functions can be readily calculated by differentiation of the basis function N_k^s(q).

There are two standard methods for the calculation of the coordinates p_k,j: i) in the collocation method one fulfills Eq. (B4 (click here)) at a number of grid points, , equal to the dimension S of the B-spline basis, ii) in the Galerkin method one defines an inner product and calculates the weak solutions which ensure that the residual:

is orthogonal to the basis:
 

With non-linear differential problems, Eq. (B4 (click here)) and Eq. (B5 (click here)) are also non-linear. They are linearized for the p_k,j and solved by iterations (Newton-Raphson method). For the sake of brevity details are omitted.

C.5.1. Collocation with the deBoor's basis.

  With the deBoor's basis, in the case of first order differential equations, the continuity of the piecewise polynomials is ensured at the mesh points but not their subsequent derivatives. Hence, the nodal vector is represented by:

and

This allows to obtain the B-spline functions shown in Fig. 8 (click here); with s=2 the scheme is similar to the centered finite difference mid-point scheme. It is clear that the continuity of the derivatives of the functions is not ensured at the mesh points. This does not mean that the functions derivatives will be discontinuous but rather that they can be discontinuous at these points. (This property has been used in the Sect. A.2 (click here).)

  
Figure 8: Normalized B-splines of order s=2 (left panel) and s=3 (right panel) calculated with deBoor basis for n=3 equidistant mesh points. The nodal vectors are indicated by crosses below both graphs

For each mesh and for each piecewise polynomial, s parameters have to be known (recall that is, on [q_i,q_i+1], a polynomial of degree s-1). The continuity of the function or the boundary conditions of the problem provide one constraint, the equations have to be written at s-1 points within each mesh. These are called the collocation points, noted , where S=(n-1)(s-1)+1 and are defined as follow:

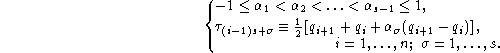
The quantities can be almost arbitrarily chosen. However, for the deBoor's nodal vector, they are chosen as the zeros of the (s-1)-th Legendre polynomial. Note that the collocation points are therefore different from the mesh points q_i; this disposition is particularly convenient at the center. For this particular collocation pattern, it can be demonstrated that, for first order differential equations, the overall approximation is of order O(h)^s, but that it is of order up to O(h)^2(s-1) at the mesh points (deBoor & Swartz 1973); here h is the size of the mesh. This is the so-called superconvergence.

Once written the differential equation on this particular basis, including boundary conditions at both ends, is formally written:
 
where for the j-th unknown is a function of q and of the vector of the coordinates p_k,j, . The resolution of the non-linear system Eq. (B7 (click here)) is obtained by linearization (Newton-Raphson method) starting from the initial model. Since the B-splines basis is a local basis, the jacobian matrix is block-diagonal. This allows storage ease and faster calculations. Here one usually uses either s=2, s=3 or s=4 for the order of the piecewise polynomials. As an example for system Eq. (21 (click here)), the linear system to be solved has then one of the following structures for s=2 (left) and s=3 (right):

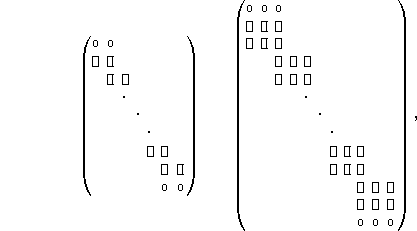
here the "" are matrix for the collocation points and the are matrix for the boundaries.

C.5.2. Basis for Petrov-Galerkin's method

  With the Galerkin type methods, the choice of the basis is more flexible. Here a basis with continuity up to for the derivatives at the grid points and (continuity) or (discontinuity) at LMR. As examples the nodal vectors with s=4 with continuity at LMR () is written:

and with discontinuity ():

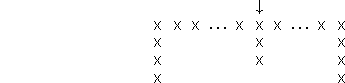
As an example from Eq. (21 (click here)) results a jacobian matrix 2s+1 bloc-diagonal of blocks. For s=2, the linear system to be solved has the following structure:

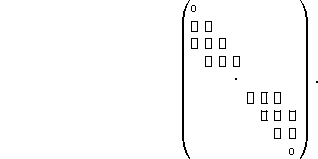
Note that the inner products between two B-splines of order less or equal to s are obtained without error with a Gaussian type integration formula with s points; the same integration formula is also used for all the inner products; the calculation of these inner products is conveniently made with the algorithm 5-22 of Schumaker (loc. cit.). Emphasize is made again on the fact that the values of the functions are not needed at the grid points, particularly at the center.

C.5.3. Solving the linearized systems

  The resolution of the linear system is performed with partial pivoting. The robustness of the solution is improved by using the modified Newton-Raphson method which is based on the fact that, for unconstrained optimization problems, the "Newton direction is a descent direction" (Conte & de Boor 1987, p. 219), giving the values of the unknown functions at iteration l+1 from their values at iteration l:
 
where are the corrections and is a parameter which ensures that the variations of the unknowns p_k,j remain small even when is large; here is adjusted in order that The iteration then stops when a sufficient accuracy is reached.