

Up: CESAM: A code
For results concerning external numerical tests using the simplified physics
of the Solar Model Comparison project (SMC)
see Christensen-Dalsgaard (1988, 1991).
Otherwise stated, the following physics is employed in numerical tests:

Figure 4: Panels a), b), c), e):
relative accuracy on the closure for,
respectively, the first four differential equations of stellar evolution; panel
d): enlargement for outer layers for the pressure gradient; panel f): relative
difference on number of baryons.
These plots are computed, using the improved solution, for more than 3500
points, randomly distributed in the model; the radius of the innermost point is
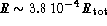 .
The accuracy of the solution is better than
.
The accuracy of the solution is better than 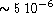 except in the
neighbourhood of the LMR and in the atmosphere
except in the
neighbourhood of the LMR and in the atmosphere
- EOS: EFF formalism (Eggleton et al. 1973).
- Opacities: 4D linear (T6,A,X,Z) interpolation of OPAL radiative
opacity
data (Rogers & Iglesias 1992) extended with Kurucz's (1991) opacity
data for low temperatures; as usual, with OPAL opacity data,
 .
.
- Convection: at each level, the Schwarzchild's criterion is employed to
decide if the energy transport is made by radiation or by convection. The basic
formulation of the classical mixing length theory according to Henyey
et al. (1965)
is used for the calculation of the convective gradient; it also
takes into account the optical thickness of the convective elements.
- Thermonuclear reactions: the nuclear network contains the following twelve
species which enter into the most important nuclear reactions of the PP, CNO
and the beginning of the
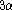 cycles chain (Clayton 1968): 1H,
2D, 3He, 4He, 7Li, 8Be, 12C, 13C,
14N, 15N, 16O, 17O; in some models, the species 2D, 7Li, 8Be are
assumed to be at equilibrium; the relevant nuclear reactions are interpolated
from the tabulated rates of Caughlan & Fowler (1988); weak screening is
assumed; the initial abundances are taken from Anders & Grevesse (1989)
meteoric abundances.
cycles chain (Clayton 1968): 1H,
2D, 3He, 4He, 7Li, 8Be, 12C, 13C,
14N, 15N, 16O, 17O; in some models, the species 2D, 7Li, 8Be are
assumed to be at equilibrium; the relevant nuclear reactions are interpolated
from the tabulated rates of Caughlan & Fowler (1988); weak screening is
assumed; the initial abundances are taken from Anders & Grevesse (1989)
meteoric abundances.
- Atmosphere: single shell approximation or restoration of an atmosphere
using a
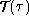 law derived from Kurucz's model atmospheres
(Morel et al. 1994).
law derived from Kurucz's model atmospheres
(Morel et al. 1994).
- Diffusion coefficient: if diffusion is not ignored, the microscopic
diffusion coefficients of Michaud & Proffitt (1993) are employed.
- Angular momentum: the rotation is ignored.
- Mass loss: the mass loss is assumed to be zero and the mass defect is
ignored.
The expansion of the unknown functions on a basis allows to recover
exactly the numerical solution at any location, i.e., not only at the grid
points. Moreover with the de Boor's choice of the collocation points
(de
Boor 1978),
the order of the accuracy of the numerical solution, at the grid points, is
improved by
superconvergence (see Appendix C2).
This nice numerical property avoids the Richarson extrapolation
(Christensen-Dalsgaard 1982) which is, with stiff problems, sometimes
unstable (Hairer & Wanner 1991).
That improvement is illustrated Fig. 3 (click here): for a
calibrated standard solar model, evolved from the PMS to the present age with
"standard accuracy" (sa), but with a constant number of shells fixed to
300, the
relative accuracy on the pressure gradient
by
superconvergence (see Appendix C2).
This nice numerical property avoids the Richarson extrapolation
(Christensen-Dalsgaard 1982) which is, with stiff problems, sometimes
unstable (Hairer & Wanner 1991).
That improvement is illustrated Fig. 3 (click here): for a
calibrated standard solar model, evolved from the PMS to the present age with
"standard accuracy" (sa), but with a constant number of shells fixed to
300, the
relative accuracy on the pressure gradient  :
:
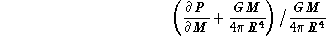
is plotted for points randomly distributed on the interval 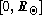 ;
as seen, the relative precision, taking advantage of the super convergence, is
improved by one order of magnitude.
Figure 3 (click here) illustrates also the stability of the numerical solution near
the center, the possibility of recovering, with full accuracy, the
numerical solution everywhere and, the significant
improvement of the accuracy in the envelope due to the superconvergence.
;
as seen, the relative precision, taking advantage of the super convergence, is
improved by one order of magnitude.
Figure 3 (click here) illustrates also the stability of the numerical solution near
the center, the possibility of recovering, with full accuracy, the
numerical solution everywhere and, the significant
improvement of the accuracy in the envelope due to the superconvergence.
For more than 3500 points randomly distributed
in a model of 1 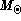 , evolved from
ZAMS to 4550My, with "Solar accuracy" (Sa), the relative differences
between left and right hand sides of the four first differential equations of
Eq. (1 (click here)), namely the derivatives
, evolved from
ZAMS to 4550My, with "Solar accuracy" (Sa), the relative differences
between left and right hand sides of the four first differential equations of
Eq. (1 (click here)), namely the derivatives  ,
, 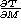 ,
,
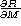 and
and 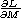 , have been computed from the improved solution of
fourth order; the results, plotted Fig. 4 (click here), allow an estimate of the
internal accuracy achieved. That model includes an atmosphere reconstructed (see
Sect. 3.2.4 (click here)) and smooth opacity data have been
provided using the bivariate rational spline interpolation scheme of
Houdek & Rogl (1996).
, have been computed from the improved solution of
fourth order; the results, plotted Fig. 4 (click here), allow an estimate of the
internal accuracy achieved. That model includes an atmosphere reconstructed (see
Sect. 3.2.4 (click here)) and smooth opacity data have been
provided using the bivariate rational spline interpolation scheme of
Houdek & Rogl (1996).
As seen, the differential equations are fulfilled within a relative
precision better than 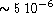 except in the neighbourhood of
the LMR at
except in the neighbourhood of
the LMR at 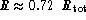 , and in the atmosphere for
, and in the atmosphere for
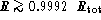 .
At LMR the local drop of the precision is a consequence of the small
discontinuity of the density, caused by the mixing in the convective zone
where the nuclear reactions, though weak, are active; there
.
At LMR the local drop of the precision is a consequence of the small
discontinuity of the density, caused by the mixing in the convective zone
where the nuclear reactions, though weak, are active; there 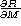 is
discontinuous, the solution is only of class
is
discontinuous, the solution is only of class 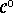 , the fourth order
accuracy cannot be reached; the effect is more sensitive for
, the fourth order
accuracy cannot be reached; the effect is more sensitive for 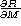 than for the other gradients, Fig. 4 (click here) panel (c). The cause of
the low accuracy
than for the other gradients, Fig. 4 (click here) panel (c). The cause of
the low accuracy  in the restored atmosphere, panel (d),
is a consequence of the non-linear dependence of the natural variable
in the restored atmosphere, panel (d),
is a consequence of the non-linear dependence of the natural variable
 , used for the restoration of the atmosphere, with respect to R through
the
, used for the restoration of the atmosphere, with respect to R through
the 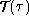 law and the opacity.
law and the opacity.
In the model, the closest grid
point from the center is located at 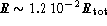 ;
in the plots, deliberately, the first point was located
at
;
in the plots, deliberately, the first point was located
at 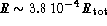 , i.e., quite near to the central singularities;
the stability of the numerical solution there is clearly illustrated
Fig. 4 (click here), panels (a), (b) (c) and (e).
, i.e., quite near to the central singularities;
the stability of the numerical solution there is clearly illustrated
Fig. 4 (click here), panels (a), (b) (c) and (e).

Figure 5: Plots, with respect to the normalized radius, of
discontinuous quantities 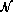 (dots) and
(dots) and 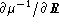 (full) -
(full) - 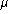 is the mean molecular weight - in the neighbourhood of the LMR
of a solar model with microscopic diffusion; on the
is the mean molecular weight - in the neighbourhood of the LMR
of a solar model with microscopic diffusion; on the 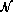 curve,
between two grid points
curve,
between two grid points  , each dot corresponds to a
calculated and not to an interpolated value of
, each dot corresponds to a
calculated and not to an interpolated value of 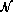
As demonstrated Appendix B4 and Appendix C4, the algorithm employed for the
calculation of the chemical composition are conservative; that is illustrated
Fig. 4 (click here) panel (f), where the local departure from the mean value of the
number of baryons,
 is plotted; ni and Ai are, respectively, the baryonic number and the
atomic weight of Xi. As seen, the conservation of the number of baryon is
ensured within the machine accuracy except at LMR, due to the mixing which is
not made with so high numerical accuracy (see Sect. 3.3.2 (click here)) and, also to the
displacement of the LMR.
is plotted; ni and Ai are, respectively, the baryonic number and the
atomic weight of Xi. As seen, the conservation of the number of baryon is
ensured within the machine accuracy except at LMR, due to the mixing which is
not made with so high numerical accuracy (see Sect. 3.3.2 (click here)) and, also to the
displacement of the LMR.

Figure 6: Evolutionary tracks of two  models computed with low
(dotted) and super (full) accuracy from PMS initial conditions to the onset of
the
models computed with low
(dotted) and super (full) accuracy from PMS initial conditions to the onset of
the 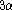 cycle. Large time steps are responsible of the angular behavior
of the solution of low accuracy; the two tracks do not significantly
differ, they are superimposed on the main sequence
cycle. Large time steps are responsible of the angular behavior
of the solution of low accuracy; the two tracks do not significantly
differ, they are superimposed on the main sequence
Figure 5 (click here) illustrates the ability to restore the solution at any location,
even with discontinuous functions. Due to the convective mixing, in a stellar
model taking diffusion into account the gradient of the mean molecular weight
(here noted 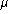 ) and the quantity:
) and the quantity:
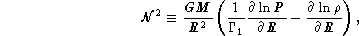
are discontinuous at LMR - 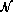 , difference between two gradients,
is equivalent to a second derivative -
, difference between two gradients,
is equivalent to a second derivative - 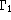 is the adiabatic exponent. In
the neighbourhood of the LMR of a model
is the adiabatic exponent. In
the neighbourhood of the LMR of a model with microscopic diffusion (Michaud & Proffitt
1993), the above discontinuous functions have been derived from the
solution, taking advantage of the superconvergence; in Fig. 5 (click here) more
than 20 point are inserted between two adjacent grid points.
Emphasize is made on the following facts: i) the discontinuity is well marked,
ii) in its vicinity, even with jumps,
for the diffusion coefficients, as large as thirteen magnitudes, the solution has
no oscillation, iii)
with microscopic diffusion (Michaud & Proffitt
1993), the above discontinuous functions have been derived from the
solution, taking advantage of the superconvergence; in Fig. 5 (click here) more
than 20 point are inserted between two adjacent grid points.
Emphasize is made on the following facts: i) the discontinuity is well marked,
ii) in its vicinity, even with jumps,
for the diffusion coefficients, as large as thirteen magnitudes, the solution has
no oscillation, iii) 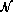 , a second
derivative, is smooth, iv) a grid point is placed right on the LMR.
, a second
derivative, is smooth, iv) a grid point is placed right on the LMR.
Two models of  have been evolved starting from PMS to the onset of
the 4He burning phase; these two models differ only by the numerical
accuracy achieved. The first one, is computed with low accuracy (la), the
second with
standard accuracy (sa), see Table 1 (click here); the numbers
of, time steps, shells at the onsets of PMS, ZAMS, POST and
have been evolved starting from PMS to the onset of
the 4He burning phase; these two models differ only by the numerical
accuracy achieved. The first one, is computed with low accuracy (la), the
second with
standard accuracy (sa), see Table 1 (click here); the numbers
of, time steps, shells at the onsets of PMS, ZAMS, POST and 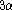 cycle
burning phase, are given Table 2 (click here). The
evolutionary tracks are notably stable, even for the rugged solution obtained
with (la); notice also that, on the main sequence,
the two tracks are superimposed.
cycle
burning phase, are given Table 2 (click here). The
evolutionary tracks are notably stable, even for the rugged solution obtained
with (la); notice also that, on the main sequence,
the two tracks are superimposed.


Up: CESAM: A code
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr


