

Up: CESAM: A code
The flow chart of CESAM takes advantage of two spaces: a functional
space (B-spline), where the differential equations are integrated with the
mathematical formalism and, a physical space, where the
equations are written regarless of the method employed for their solution; it
ensues a modular structure which allows to exploit, with the same algorithm,
several sets of physical data, e.g.
EOS, opacity, thermonuclear reactions, diffusion, atmosphere, etc...\
and a few numerical parameters allow to adjust the order and the accuracy of
the solution.
The iterative process is initialized with a
model which is, either, for t=0, a starting model of PMS or ZAMS or,
for t>0, a previously evolved model;
a new initial model is then computed with the requested open parameters for
physics, i.e., mass, mixing length, etc... and for numeric, i.e., number of shells,
order of piecewise polynomials etc...\
Along the evolution, the calculation of a new model is initialized with the
previous model without extrapolation.
When the gravothermal energy is the leading term in the energy equation, such
as occurs during the PMS phase or with shell sources,
the values for density and specific internal energy need to be accurately
initialized (Kippenhahn et al. 1968); since the approximate model is the previous
one, the initial value for the gravothermal energy is zero, the energy
equation
is strongly in error and the Newton-Raphson scheme does not converge. The
remedy of Härm & Schwarzchild (1966), consists in taking the
approximate model as the previous one shifted in mass; in the B-splines space,
this technique is not
easy to be worked out and, by experience, it does not work for PMS. A trivial
solution has been found: for the first Newton-Raphson
iterate,
but only for this first, the gravothermal energy is taken equal to its
value in the former model; hence the energy equation remains in almost closed
form (recall that
is one of the necessary conditions for the convergence of the Newton-Raphson
method).
There are three levels of time step controls; as soon as one of the
following criteria is not fulfilled the time step is divided by two,
otherwise, for the next model it increases, at most, by 20%:
- inadequate accuracy of the solution or no convergence
of the IRK scheme, after more than 12 Newton-Raphson iterations,
- slow convergence or divergence of the Newton-Raphson scheme
used for the two points boundary problem,
- too large changes in chemicals,
- too large gravothermal energy change.
The amount of calculations increases with the accuracy to be achieved, for some
applications precise models are not necessarily needed, e.g. with uncertain or
unstable physics; for others applications, high accuracy is reachable and is of
necessity, e.g. calibrated solar models used for
the calculations of frequencies; therefore the
numerical parameters have to be adjusted to the aims towards the model is
directed. Table 1 (click here) gathers three sets of numerical parameters of common use:
i) (la) low accuracy, for tests, uncertain or unstable physics, ii) (sa)
standard accuracy, iii) (Sa) Solar accuracy, for the
calculation of precise solar models.
In Table 1 (click here), C is the repartition constant, 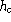 the order of
piecewise polynomials employed for interpolation of chemicals with (in
parenthesis) their values with diffusion; p is the order of the IRK scheme;
the order of
piecewise polynomials employed for interpolation of chemicals with (in
parenthesis) their values with diffusion; p is the order of the IRK scheme;
 is the maximum relative change allowed for 1H and 4He
during a time step of maximum length
is the maximum relative change allowed for 1H and 4He
during a time step of maximum length 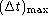 ;
; 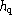 is the order of
piecewise polynomials of the solution with (in parenthesis),
their orders magnified by super
convergence (see Sect. 5.2 (click here));
is the order of
piecewise polynomials of the solution with (in parenthesis),
their orders magnified by super
convergence (see Sect. 5.2 (click here));  is the closure used for the damped Newton-Raphson
scheme;
is the closure used for the damped Newton-Raphson
scheme; 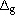 is the maximum relative change allowed to the gravothermal
energy in the core during a time step;
is the maximum relative change allowed to the gravothermal
energy in the core during a time step; 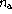 and
and 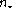 respectively
are the total number of shells in the atmosphere and between the bottom of the
atmosphere and the level where the radius of the star is located;
respectively
are the total number of shells in the atmosphere and between the bottom of the
atmosphere and the level where the radius of the star is located; 
 ,
, 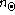 respectively are typical numbers of shells in solar
model at the onset of the PMS, of the ZAMS and for the present solar age.
respectively are typical numbers of shells in solar
model at the onset of the PMS, of the ZAMS and for the present solar age.
The solar models are calibrated by
adjusting the ratio  of the mixing-length to the
pressure scale height,
the initial mass fraction X of
hydrogen and the initial mass fraction Z/X of heavy elements to hydrogen in
order to have, at present day, the luminosity
of the mixing-length to the
pressure scale height,
the initial mass fraction X of
hydrogen and the initial mass fraction Z/X of heavy elements to hydrogen in
order to have, at present day, the luminosity 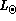 , the radius
, the radius  and the mass fraction
and the mass fraction  . According to
Guenter et al. 1992 the most
recent determinations for the solar luminosity, radius, mass and age are:
. According to
Guenter et al. 1992 the most
recent determinations for the solar luminosity, radius, mass and age are:
 erg s-1,
erg s-1,
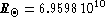 cm,
cm,
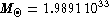 g, and
g, and  Gy.
The value of the ratio of heavy elements to hydrogen, at present day is,
Gy.
The value of the ratio of heavy elements to hydrogen, at present day is,
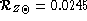 (Grevesse & Noels 1993;
Noels et al. 1995).
(Grevesse & Noels 1993;
Noels et al. 1995).
With the microscopic diffusion coefficients of Michaud & Proffitt (1993), the
following dependences on the initial PMS values of the unknown parameters has
been
found:
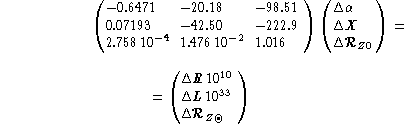
with 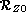 as the value of Z/X at t=0 and
as the value of Z/X at t=0 and 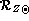 its value at present solar age.
Along the calibration process the matrix of the dependence can be updated, using
the one rank Broyden's method (Conte & deBoor 1987, p. 222)
its value at present solar age.
Along the calibration process the matrix of the dependence can be updated, using
the one rank Broyden's method (Conte & deBoor 1987, p. 222)

Figure 3: Comparison of the relative accuracy on the pressure gradient
between the numerical solution and its improvement taking advantage of
the super convergence. Clearly one order of magnitude is acquired. One
also emphasizes on the good behavior of the solution in the vicinity of the
center


Up: CESAM: A code
Copyright by the European Southern Observatory (ESO)
web@ed-phys.fr
![]() the order of
piecewise polynomials employed for interpolation of chemicals with (in
parenthesis) their values with diffusion; p is the order of the IRK scheme;
the order of
piecewise polynomials employed for interpolation of chemicals with (in
parenthesis) their values with diffusion; p is the order of the IRK scheme;
![]() is the maximum relative change allowed for 1H and 4He
during a time step of maximum length
is the maximum relative change allowed for 1H and 4He
during a time step of maximum length ![]() ;
; ![]() is the order of
piecewise polynomials of the solution with (in parenthesis),
their orders magnified by super
convergence (see Sect. 5.2 (click here));
is the order of
piecewise polynomials of the solution with (in parenthesis),
their orders magnified by super
convergence (see Sect. 5.2 (click here)); ![]() is the closure used for the damped Newton-Raphson
scheme;
is the closure used for the damped Newton-Raphson
scheme; ![]() is the maximum relative change allowed to the gravothermal
energy in the core during a time step;
is the maximum relative change allowed to the gravothermal
energy in the core during a time step; ![]() and
and ![]() respectively
are the total number of shells in the atmosphere and between the bottom of the
atmosphere and the level where the radius of the star is located;
respectively
are the total number of shells in the atmosphere and between the bottom of the
atmosphere and the level where the radius of the star is located; ![]()
![]() ,
, ![]() respectively are typical numbers of shells in solar
model at the onset of the PMS, of the ZAMS and for the present solar age.
respectively are typical numbers of shells in solar
model at the onset of the PMS, of the ZAMS and for the present solar age.
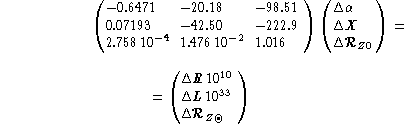
![]() as the value of Z/X at t=0 and
as the value of Z/X at t=0 and ![]() its value at present solar age.
Along the calibration process the matrix of the dependence can be updated, using
the one rank Broyden's method (Conte & deBoor 1987, p. 222)
its value at present solar age.
Along the calibration process the matrix of the dependence can be updated, using
the one rank Broyden's method (Conte & deBoor 1987, p. 222)
