For data reduction both interferometric signals are processed
independently. We shall consider only one of them, which will help us
simplify the notations as we can then drop index i. Thus for example,
when the recombination is incoherent the wide band interferometric signal
can be expressed as
where the 
are the proportionality factors detailed in
Sect. 4 (click here).
To establish an expression of the intensity after coherent recombination in
the X coupler, we first describe the monochromatic interferogram at wave
number 
; the wide band interferogram will then be obtained by
integration over the optical bandpass of the system.
At the recombination point in the correlator the complex representations of
the electric fields of the two guided beams have the general expression:
and
where 
is the angular pulsation and 
the
phase accumulated from the source to the recombination point through
channel i. The correlator sums the instantaneous amplitudes of the
electric fields and the instantaneous amplitude at its output is:
What is measured by the observer is a quantity proportional to the average
(over a period much greater than the coherence time of the radiation) of
the squared modulus of the amplitude:
The quantity 
is the complex degree of
coherence (Goodman 1985) between the signals collected by each
fiber. Here because the source is by definition monochromatic (with an
optical frequency 
and a wave number 
), the complex degree of
coherence takes the simplified form of an oscillating function of the delay
between the two waves:
where 
is the
complex coherence factor between the two beams at the recombination point.
It is the product of the complex object visibility V
at the input (the entrance
pupils) of the interferometer by an instrumental transfer function
T
:
According to the Van Cittert-Zernike theorem (Born & Wolf 1980;
Goodman 1985), the quantity V
is also
the monochromatic complex visibility of the object at the spatial frequency
corresponding to the interferometric baseline vector. The modulation
transfer function 
of the instrument expresses
mainly the frequency response of the detectors and a coherence loss due to
polarization mismatch in both radiations. The phase term
includes dispersion in the guided optics
components (Coudé du Foresto et al. 1995), and possible
differential phase jumps when reflecting on telescope mirrors.
It should be emphasized that the transfer function, as defined here, is
purely instrumental and does not involve atmospheric turbulence. Assuming
that the instrument is stable enough, the impulse response of the system
can be calibrated on a reference object whose complex visibility V
is well known (it can be for example an unresolved point source for which
V
). If 
is the complex coherence factor measured on the reference, the instrumental
transfer function is
The modulus and phase of the Fourier transform of the object are then given by
Let us now return to the general expression of the interferogram
(Eq. 25 (click here)), which can be rewritten, with
relation 26 (click here) in mind,
Thanks to the results of the previous section (Eqs. 9 (click here), 12 (click here) and 15 (click here)), we can relate the
squared monochromatic amplitudes of the fields, which cannot be accessed
directly, to the photometric signals 
and 
which are measurable
quantities:
Defining 
and 
, we
have for the cross term:
Since the photometric signals 
and 
vary with time (i.e., with
the OPD x), the monochromatic interferogram can be written as:
It is the sum of the scaled photometric signals (an additive scintillation
noise) and a sinusoid whose amplitude is modulated by the geometric average
of the injection efficiencies (a multiplicative noise).
The wide band interferogram is calculated by integration of the
monochromatic signals over the optical bandpass:
After having extended to negative wave numbers the validity range of all
functions of 
(their value is set to 0 for 
),
Eq. (34 (click here)) yields:
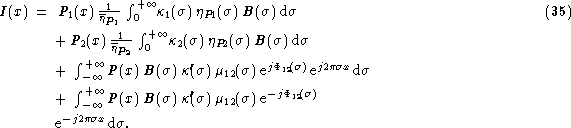
The first two lines of Eq. (35 (click here)) are related to the
wide band scintillation noise. The last two lines can be identified with an
inverse Fourier transform, and the multiplicative noise of the fringe
signal in the OPD space becomes a convolution in the wave number space:
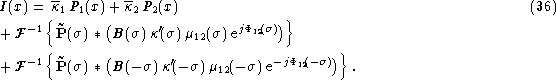
In what follows we will use either the symbol 
or the tilde
for the Fourier transform (FT) operation. The FT of
the interferometric signal is:
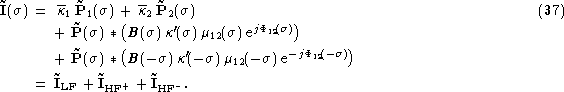
If the OPD scanning speed is fast enough for the fringe frequency to be
larger than the bandwidth of the coupling fluctuations (typically a few
tens of Hz), then the interferogram has two distinct components in the
frequency space:
Figure 3: An example of a time sequence, with the interferometric signal
I(t) and the two photometric signals 
and 
. Scanning
speed is 359
m/s. The duration of the recorded scan is 1.024s but
only the central 0.6s is displayed here to better show the fringes
Figure 4: Modulus of the Fourier Transform of I(t), showing the low
frequency scintillation noise and the interferometric signal at a higher
frequency
An example of interferogram obtained on Arcturus is shown Fig. 3 (click here), while its one-sided amplitude spectrum is in
Fig. 4 (click here). During the scan 1024 points have been
recorded at a sampling rate of 1kHz. In the time sequence, the number of
fringes is substantially larger than what might be expected from an
interferogram obtained with a K band filter. This is caused by chromatic
differential dispersion in the waveguides, which affects the phase part
of the instrumental transfer function, but not its amplitude
, and therefore does not have consequences on visibility measurements
(Coudé du Foresto et al. 1995). The amplitude spectrum shows
the contribution of scintillation noise at low frequencies (
Hz)
and the fringe signal at higher frequencies. The spectral width at half
maximum of the scintillation noise being only a few Hertz, the convolution
broadening of the fringe signal is very small. What is better seen here in
the fringe signal is the effect of differential piston, which corrupts the
Fourier relationship between the fringe pattern in the OPD (time) domain
and the spectral intensity distribution of the source. Here the nominal
fringe speed is 
m/s, which corresponds to fringe frequencies
ranging from 150Hz (for 
m) to 180Hz (for 
m). However, because of piston phase perturbations the fringe
signal is spread substantially beyond this nominal frequency range, and
presents deep spectral features that cannot be attributed to the real
spectroscopic lines of Arcturus, a standard K2III star.