The aim of this section is to determine, when photometric intensities 
and 
are recorded at the outputs of the Y couplers, what are the
actual intensities of the beams that are being correlated in the X coupler.
We need to establish what proportionality factors link the outputs of the
interferometric X coupler and the outputs of the photometric Y couplers. So
for this section it is assumed that the recombination is fully incoherent.
The monochromatic signal produced at any given time by the photometric
detector 
(
) is proportional to its overall gain
and to the transmission 
of the coupler 
towards the output 
:
For what follows it is convenient to introduce the global efficiency
of the photometric channel 
:
which leads to
The signal provided by the interferometric detectors 
and 
is
proportional to the optical powers 
and 
at the output of the
X coupler, and to the gain of the photometers:
Optical powers at the inputs and outputs of X are linked by a transmission
matrix:
where 
is the transmission of the coupler 
towards the X coupler, and 
is the transmission
of the X coupler from input (telescope) j towards output i.
Here it should be noted that, since most fiber couplers are chromatic (and
because of aging processes, their chromaticism can evolve over the years),
the coefficients 
and 
are 
-dependent and cannot be known with a sufficient
accuracy. There is also no way to access the raw coupling efficiencies.
Thus the only matrix that can actually be measured links the photometric
signals to the interferometric signals:
Combining the relations 7 (click here), 11 (click here) and 12 (click here) leads to
The wide band photometric relationships are obtained by integration
over 
. For the 
detectors:
From this follows:
where
is the global wide band efficiency of the photometric channel 
.
According to Eq. (12 (click here)), the monochromatic signal
provided by detector 
is linked to 
and
by
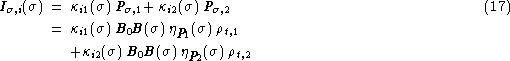
and an integration yields
Thus a linear relationship links the two wide band signal pairs:
with:
Figure 2: The 
(+)
and 
(
) coefficients, as measured on
Boo (Arcturus) in a batch of 122 scans
The main interest of the (
) transfer matrix is that
it can be evaluated directly from the data, without requiring an a priori
knowledge of the individual transmissions and gains in the system. The
evaluation is performed by adjusting a least square fit of a linear
combination of 
and 
to 
for the 
,
and to 
for the 
. Figure 2 (click here)
shows an example of a series of measurements of 
and 
. In order to reduce statistical errors, for
each 
all measurements in a batch are averaged to
produce the value adopted for the rest of the data reduction procedure.