6. Deriving the fringe visibility from aninterferogram

  The expression 37 (click here) is the basis on which will be derived the coherence factor between the two beams. In a first step we need to correct the interferogram from the turbulence induced modulation of the fringe pattern; then we can derive an expression of the coherence factor that does not depend on turbulence.

6.1. Correcting the interferogram

  The first operation consists in separating the low- and high frequency components of the signal, to isolate the interferometric signal from the scintillation noise. This is best achieved by a subtraction in the OPD space:

It is known from Eq. (37 (click here)) that in the wave number space is written as:
 
which yields by inverse Fourier transform in the OPD domain, where the convolution by the scintillation noise becomes a product:

Dividing by P(x) and going back to the wave number space help us establish an interferometric signal which is corrected from the atmosphere induced fluctuations:
 
The factor 1/2 was introduced to normalize to 1 the integral of the modulus of in the canonical case where and .

  
Figure 5: The interferogram of Fig. 3 (click here), after correction

Figure 5 (click here) shows the corrected sequence corresponding to the interferogram of Fig. 3 (click here).

6.2. Double Fourier mode

 

From the relationship (41 (click here)), and after calibration of the instrumental transfer function, can be measured the product V of the object complex visibility by its spectral intensity. To obtain this result, which is at the basis of double Fourier interferometry (Itoh & Ohtsuka 1986; Mariotti & Ridgway 1988), three conditions need to be fulfilled:

1. The instrumental response needs to be perfectly known. We have seen that the complex transfer function T could be measured on a reference star; the coefficient needs also to be calibrated (on a reference star or an internal source);
2. The differential piston between the two pupils must be removed;
3. The decoupling of time and wavelength in the injection efficiency must be effective.

Because it combines spectral information with high angular resolution, the scientific potential of double Fourier interferometry is considerable as it fully exploits the fundamentally tridimensionnal nature of interferometric data. While the spatial coherence of the source (the 2D FT of the object intensity distribution) is explored by the double pupil of the interferometer, its temporal coherence (the 1D FT of its spectral distribution) is explored by the scan around the zero OPD. One can also use the generalized version of the Van Cittert-Zernike theorem (Born & Wolf 1980), and say that the mutual coherence of the collected beams is linked by a tridimensionnal FT to the spatio-spectral intensity distribution of the object. In the type of interferometer we consider here, each interferogram can in principle lead to the measurement of one line in the interferometric data cube. Although interferometric data cubes are familiar to radio astronomers (Perley 1985), dealing with them in the context of optical and infrared observations is quite new: one can consult Claret et al. (1991) for a first approach.

6.3. The wide band coherence factor

In all data obtained so far, there is no piston compensation and the phase information in the interferogram is lost. Acknowledging this situation, we shall concentrate on the squared modulus of the Fourier transform, which is the spectral power density of the corrected interferometric signal:
 

  
Figure 6: Spectral power density of the corrected interferogram

It is clear, however, that Eq. (42 (click here)) remains an idealization because it does not take into account the piston which perturbs the Fourier relationship. Thus we should not hope that it holds for each ; however, provided that the piston is not too strong, we can assume that it only redistributes the fringe energy in the power spectrum, so that the relationship (42 (click here)) is valid in an integral form:
 
Any departure from this approximation will be referred to as ``piston noise'', and we will see in Sect. 7.3 (click here) how its relative importance as a noise source can be evaluated.

Now if is the integrated value, weighted by , of the squared modulus of the coherence factor:

then can be deduced from S thanks to the relationship
 

6.3.1. The shape factor

From Eq. (45 (click here)) it appears that the value of depends on a weighting factor
 
which is intrinsic to the photometric behavior of the system and to the spectral intensity distribution of the source.

In practice, the quantity of interest is not the coherence factor per se but the visibility of the source, which is obtained after the interferometer has been calibrated on a reference whose visibility is well known. From the relationships (28 (click here)) and (29 (click here)), the modulus of the object visibility is given by:

and the weighting factor disappears in the calibration process if the source and the reference have the same spectral intensity distribution. Thus, provided the reference is adequately chosen, the determination of F is not critical.

  
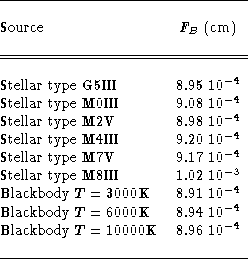
Table 1: Shape factor computed for different sources, observed with a standard K filter. For the stellar types, the calculation was based on infrared FTS spectra (Lançon & Rocca-Volmerange 1992)

Usually the coefficient F cannot be established directly because the quantity , defined by Eq. (32 (click here)):

is difficult to measure at all wave numbers. We can make the reasonable approximation that is achromatic and for all wave numbers

This assumption holds all the better as the couplers are less chromatic, but it is never rigorously true because of the chromaticism of the injection efficiency that is included in the coefficients (the global efficiency of the photometric channels). Nevertheless, any departure from the approximation can be seen, in the first order, as a purely instrumental effect, which is then included in the transfer function .

Once has been set to a constant value the determination of F is equivalent to the determination of another factor, , which involves the source only and is defined by

It will be called the shape factor because it depends on the shape of the normalized spectral intensity distribution:

Some numerical values of are given in Table 1 (click here) for different types of sources observed with a standard K filter. The deeper the spectral features of the source, the larger the value of . But if we except the very late type class M8III, the relative variation of the shape factor with the stellar spectral class is contained within 3%. For a blackbody, depends very little on the temperature.