In Paper I the use of synthetic, noise-free spectra implied zero random errors, and enabled us to examine the mismatch shifts obtained for a number of quite small windows. With observed spectra, however, the presence of noise gives rise to random errors that are correlated with window size. We therefore concentrate this discussion on the RV shifts measured with the widest windows, where the random errors should be smallest, i.e. Windows 1 (everything included) and 3 (only the problematic Balmer lines and CaII K line blocked out). We offer in Sect. 5.6 an appraisal of the other windows that were tested.

Because the wavelength scale of each observed spectrum is in its own rest-frame, the only discernible RV shift between object and template is attributable either to random and/or systematic errors, or to spectrum mismatch. Figure 3 shows one sub-set of RV shifts that were measured for the stars in our sample when (as far as we could ascertain) the total internal error was minimized. The latter is estimated as 0.15 kms^-1 (Sect. 4.2.2), of which no more than 0.1 kms^-1 is due to systematic errors in the wavelength scale (Sect. 3.6).

In order to interpret the residual RV shifts, and especially the curvature, shown in Fig. 3, we must first confirm the generality of the results, or discover whether any significant contribution is caused in some way by the very nature of the spectral lines in Sirius. We therefore sought to reproduce the shape of the mismatch curves in Fig. 3 by three different routes: (a) by investigating star-to-star mismatch shifts, i.e. keeping the temperature differences $\Delta$ $T_{\rm eff}$ to a minimum, and (b) by using different stellar spectra as the template. We also examined the effects of replacing the stellar spectra with synthetic spectra calculated for comparable values of $T_{\rm eff}$ , choosing as a template a model whose $T_{\rm eff}$ was near that of Sirius.

Keeping $\Delta$ $T_{\rm eff}$ to a minimum

We cross-correlated pairs of spectra of stars that are neighbours in Table 1, thereby minimizing $\Delta$ $T_{\rm eff}$ . The results, shown in Fig. 5, exhibit the pattern one would expect from a sequence of totally unrelated cross-correlations between spectra which are basically at rest with respect to one another: the mean of all the shifts is obviously very close to zero, while individual shifts are scattered around that mean. Again, the amplitude of the scatter is much larger that the expected random error so it must be due mainly to spectrum mismatch. If the curvature which is visually apparent in Fig. 3 reflects some property of the object spectra themselves, in Fig. 5 it should leave a signature in the form of a monotonically rising trend underlying the scattered shifts, but none such is apparent. We conclude therefore that a major contribution to the said curvature originates in the nature of the Sirius template.

However, if we examine the differences between successive shifts in Fig. 3 (also to be read from Table 3), we notice that the sign of those differences is mostly the same as the sign of the corresponding shifts in Fig. 5. Taking that notion a step further, we have calculated the sample correlation coefficient ( CC) between the differences between successive shifts with respect to Sirius (excluding those involving Sirius itself) and the shifts in Fig. 5; its value is 0.71 and is evidence, at the 5% significance level, of a positive correlation between the two sets.

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.steps.eps}}\par\end{figure}$

Figure 5: RV shifts determined by cross-correlating pairs of adjacent spectra as listed in Table 1. Each horizontal bar illustrates the level of a measured shift and the (B-V) interval in question. The horizontal dotted bars represent the corresponding shifts when one of each pair of spectra has (if necessary) been rotationally broadened slightly so that its line widths match those of the other star in the pair. The sets of bars have been conjoined at their midpoints to improve clarity. Note that the application of broadening tends to increase the scatter

5.1.2 Using other spectra as the template

The return of the curve in Fig. 3 towards zero at the coolest end of the plot suggested that the coolest star in our sample ( $\iota$ Psc) might have enough spectrum lines in common with much hotter stars to constitute a useful template, notwithstanding the large $\Delta$ $T_{\rm eff}$ involved. We therefore selected new templates to represent the full range of $T_{\rm eff}$ examined: (a) $\iota$ Psc (F7V), (b) 14 Del (A1V) and (c) 21 Peg (B9.5V). The results are shown in Fig. 6, where the thick lines are the same as those in Fig. 3 for Sirius. In Table 3 we list the RV shifts measured, for Window 3 only, with the four different templates.

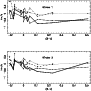$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.comps.eps}}\par\end{figure}$

Figure 6: Comparisons of mismatch curves measured using different templates. Thick line: Sirius template (see Fig. 3), dashed line: $\iota$ Psc (F7 V), dotted line: 14 Del (A1 V), thin line: 21 Peg (B9.5 V). The illustration has been limited to Windows 1 and 3; other windows showed similar trends but with larger scatter owing to the dominance of a few blends

Table 3: RV shifts derived by cross-correlating the programme stars against 4 different templates, using Window 3
RV shifts (kms^-1)

Template

Star Sp. B-V Sirius $\iota$ Psc 14 21

type Del Peg

64 Ori B8III -0.11 -0.11 0.53 0.29 0.03

HR 8094 B9V -0.10 -0.01 -0.07 0.24 -0.04

HR 7664 B9p -0.08 -0.43 -0.29 -0.09 -0.37

$\phi$ Her B9p -0.07 0.35 0.26 0.73 0.28

21 Peg B9.5V -0.07 0.17 0.23 0.26

$\beta^2$ Cap B9.5 -0.02 0.07 0.07 0.13 -0.09

o Peg A1p -0.02 -0.11 0.07 0.13 -0.14

Vega A0V 0.00 0.20 -0.75 0.40 -0.36

$\gamma$ Gem A0IV 0.00 -0.15 0.00 0.26 -0.36

Sirius A1m 0.01 -0.11 0.33 -0.17

14 Del A1V 0.02 -0.33 -0.04 -0.26

HR 104 A2V 0.03 -0.37 0.00 0.07 -0.20

60 Leo A1m 0.05 -0.28 0.00 0.22 -0.45

95 Leo A3V 0.11 -0.55 -0.21 -0.03 -0.32

32 Aqr A5m 0.23 -0.66 -0.02 -0.02 -0.40

$\iota$ Psc F7V 0.51 0.10 0.04 -0.23

**Table 3:** RV shifts derived by cross-correlating the programme stars against 4 different templates, using Window 3
			RV shifts (kms^-1)
			Template
Star	Sp.	B-V	Sirius	$\iota$ Psc	14	21
	type				Del	Peg
64 Ori	B8III	-0.11	-0.11	0.53	0.29	0.03
HR 8094	B9V	-0.10	-0.01	-0.07	0.24	-0.04
HR 7664	B9p	-0.08	-0.43	-0.29	-0.09	-0.37
$\phi$ Her	B9p	-0.07	0.35	0.26	0.73	0.28
21 Peg	B9.5V	-0.07	0.17	0.23	0.26
$\beta^2$ Cap	B9.5	-0.02	0.07	0.07	0.13	-0.09
o Peg	A1p	-0.02	-0.11	0.07	0.13	-0.14
Vega	A0V	0.00	0.20	-0.75	0.40	-0.36
$\gamma$ Gem	A0IV	0.00	-0.15	0.00	0.26	-0.36
Sirius	A1m	0.01		-0.11	0.33	-0.17
14 Del	A1V	0.02	-0.33	-0.04		-0.26
HR 104	A2V	0.03	-0.37	0.00	0.07	-0.20
60 Leo	A1m	0.05	-0.28	0.00	0.22	-0.45
95 Leo	A3V	0.11	-0.55	-0.21	-0.03	-0.32
32 Aqr	A5m	0.23	-0.66	-0.02	-0.02	-0.40
$\iota$ Psc	F7V	0.51	0.10		0.04	-0.23

Several features of Fig. 6 stand out:
(i) All curves define a similar relationship that is nearly flat or slightly dish-shaped with a steeper gradient for (B-V) < 0.1. (That commonality incidentally demonstrates a degree of objectivity in the results).

(ii) There is a marked similarity between the curves for $\iota$ Psc and 14 Del, suggesting that an F-type template can be used reliably with early A-type spectra and that one can thus build the necessary links between the zeroes of the early-type and late-type scales. The similarity in shape between the curves for $\iota$ Psc and 21 Peg suggests that a series of such links can also be extended to B-type spectra.

(iii) Again using Table 3 to calculate the difference between successive shifts, we find that the differences obtained with 14 Del as the template correlate even better with the points in Fig. 5 than do those obtained with the Sirius template ( CC = 0.86, indicating a positive correlation at the 1% significance level). On the other hand, similar CCs for the other two templates (21 Peg and $\iota$ Psc) are 0.46 and 0.15 respectively, offering no evidence of correlation at all, possibly because of the relative extremeness of their spectral types.

(iv) There is a strong tendency for the curves for Sirius and 21 Peg to lie below the other two, and for the Sirius one to show more curvature than the other three. Other windows (not illustrated) showed the same behaviour, despite a tendency for mismatch effects caused by individual blends to dominate.

5.1.3 Tests with synthetic spectra

In order to verify our methodology, we selected models with $T_{\rm eff}$ from 7000 $\times$ 500 to 13000 K (all with logg = 4.0) from the set used in Paper I, and cross-correlated them against the model for 9000 K (corresponding roughly to A2 V) without truncation. Because the models did not include rotation, little mismatch shift was discernible; for Window 3 the curve mimicked the upturn at the hot end of the corresponding cross-correlations between stellar spectra (e.g. Fig. 6), but with only 10% of the amplitude.

5.2 Modelling the results for the Sirius template

The tests carried out above have not reproduced the curvature that is so prominent in the mismatch relation derived with our Sirius template. In fact, the 14 Del template produced a mismatch curve that is much closer to the flat result (zero RV shift) that was obtained with the synthetic-spectrum template. Use of the B9.5 template (21 Peg) resulted in a trend that was also flat, similar to that for 14 Del but displaced downwards from it (and from zero) by about 0.3 kms^-1. We also note, with some surprise, that the results seem not to depend very critically upon the magnitude of $\Delta$ $T_{\rm eff}$ .

The differences in the mismatch shifts that were generated with the Sirius and 14 Del templates were also surprising. It is important to find the reason(s), since it is only through a more general understanding of the situation that we will derive with confidence the intrinsic mismatch shifts between different stars of this spectral range. 14 Del was chosen for the test in Fig. 6 because of its close resemblance to Sirius in (B-V) and spectral type (the Am peculiarity of Sirius is described as "mild''). The only pronounced dissimilarity between these two stars is their projected rotational velocities, as is visually evident from our spectra; Sirius has vsiniof about 17 kms^-1, while that of 14 Del is about 6 kms^-1. To discover whether the obvious differences between the Sirius and 14 Del curves in Fig. 6 could be an artefact of the greater projected rotation of Sirius, we created a template of 14 Del that was blurred by a rotational velocity of 20 kms^-1 and cross-correlated the other spectra against it in the habitual fashion. The result is shown in Fig. 7, and is striking. To a first order, all of the excess curvature arising from using the Sirius template can be explained by the rotation of Sirius. Stellar rotation is therefore liable to cause a significant increase of the mismatch shift between two (even slightly) dissimilar spectra, even for rotational velocities of about 20 kms^-1, which are very modest by A-type standards. We amplify that statement further in the following section.

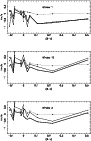$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.14del.eps}}\par\end{figure}$

Figure 7: Reproducing the Sirius mismatch curve. The heavy line is the curve for Sirius, while the dotted line represents the curve for 14 Del (see Fig. 6). The thin line shows the results obtained when 14 Del is spun by a rotational velocity of 20 kms^-1. In all three windows illustrated here, and in the top one in particular, our model of a moderately rotating A1 star reproduces closely both the curvature and the details of the Sirius curve

5.3 Spectrum mismatch and stellar rotation

In the case of noise-free synthetic spectra, and in the absence of other causes of spectrum mismatch, rotational mismatch has been shown to produce only neligible systematic errors (Verschueren 1991). Using numerical simulations Verschueren & David (1999) argued that, in order to keep the random error of the measurement of the CCF peak position close to its lower bound, it is nevertheless advisable to use a template whose rotational broadening matches that of the object.

For the studies of observed spectra in this paper we had deliberately selected sharp-lined stars with projected rotations not exceeding 20-25 kms^-1. Most have lines sufficiently narrow that the MgII doublet at $\lambda$ 4481Å is partially resolved, though in Sirius and Vega that feature is a smooth blend; thus the range of $v_{\rm rot}$ in our sample is far smaller than even the individual velocity steps (50 kms^-1) employed by the two papers cited above. Nevertheless, in view of the high resolution of our spectra we supposed initially that we might decrease the error in the CCF position by making object and template spectra match in apparent rotational velocity. However, in the case of observed spectra that premise seems to have been at least partly ill-founded, as was adumbrated by Fig. 5: the dotted lines there indicate the effects of applying a small amount ( $\le$ 15 kms^-1) of rotational broadening to one member of each pair of spectra prior to cross-correlation in order to improve the visual fit. The overall result of almost zero trend is the same in both cases, but the scatter has been made worse - i.e. the mismatch shifts have increased - by applying the broadening even though the line profiles then looked to be more similar.

We went on to test the generality of the above results by imposing different amounts of rotational broadening upon a series of cross-correlations that used first Sirius and then 14 Del as the template. In each case we broadened the template from 10 to 40 kms^-1 in steps of 10 kms^-1, and worked with Windows 1, 3 and 7. We show in Fig. 8 the results obtained (for Window 3) with the two templates: Sirius (Fig. 8a) and 14 Del (Fig. 8b). From there we draw the conclusion that any tinkering with the natural line-widths of the template, particularly in cases of very narrow lines, is liable to increase the mismatch shift.

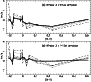$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.spins.sirius.eps}}\\ \resizebox{8cm}{!}{\includegraphics{fig.spins.14del.eps}}\\ \par\end{figure}$

Figure 8: RV shifts measured by cross-correlating test spectra against a) Sirius and b) 14 Del, when the template has been rotationally broadened up to 40 kms^-1 in steps of 10 kms^-1. The heavy line in a) is the same as that in Fig. 3, while the heavy line in b) is the same as the dotted line in Fig. 7. Thin line: broadened by 10 kms^-1 (scarcely distinguishable from the thick line); dot-dashed line: 20 kms^-1; dotted line: 30 kms^-1; dashed line: 40 kms^-1. These plots illustrate the results obtained for Window 3; the other windows yielded results that were qualitatively similar

In view of the finding that even very slight differences in spectral structure or line shapes between object and template are liable (depending on their nature and on the rotational velocities involved) to cause a systematic RV error that is well above the expected level of the random error, we can now understand why the theoretical studies did not predict this result: the conclusions of Verschueren & David (1999) were based on an investigation of synthetic spectra in which object and template were intrinsically identical.

In concluding this discussion on the effects of rotational broadening, we recall that the purpose of this series of papers is to specify a set of conditions, or limits to a general procedure, for measuring radial velocities in hot stars to a high precision and accuracy, and that one likely application will involve numerous, real-time measurements of stars in clusters for statistical analyses. An efficient system must avoid the need to determine precisely the projected rotational velocity of each individual star in order to select the best matching template. Even though the question regarding the possible reduction in accuracy due to a difference in rotation is unanswered in the case of non-identical spectra - and is likely to remain so until there is a centroiding algorithm for an asymmetrical CCF peak which can be shown to keep the random error close to its lower bound (see Verschueren & David 1999) - one must bear in mind the risk of severely decreasing the accuracy by increasing the rotation (whether artificially or through selection) in order to match the line widths of template and object. At least for spectra of a quality comparable to ours (high but not atypical S/N ratio and resolution) it has been shown (Figs. 5, 7 and 8) that rotational matching is not only unnecessary but actually harmful to the final quality of an RV measurement.

Our conclusions (Sect. 5.7) regarding the overall magnitude and sign of mismatch shifts for observed spectra are therefore based on the use of the spectrum of 14 Del, not Sirius, as the template.

5.4 How critical is the spectral type of the template?

In Fig. 9 we have repeated the series of cross-correlations performed earlier (see Fig. 3) but using 14 Del as the template. Because the results for Vega do not assist in clarifying any general trends, they have been omitted. In the bottom panel the mismatch curve has been "tidied up'' by omitting the spectra of the chemically-peculiar B stars as well, for reasons that are amplified in Sect. 5.7. The deviation shown there is less than 0.1 kms^-1 between spectral types mid-F to A3 or A2, but rises fairly abruptly to about 0.3 kms^-1 for spectral types A0 - B9. We note parenthetically that a spectral-type sub-class is equivalent to a somewhat larger $\Delta$ $T_{\rm eff}$ at late B than at mid A, so the trend with increasing $T_{\rm eff}$ is actually less abrupt than is depicted.

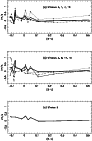$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.finala.eps}}\\ \resizebox{8cm}{!}{\includegraphics{fig.finalb.eps}}\\ \par\end{figure}$

Figure 9: The results of cross-correlating the spectra against that of 14 Del, for different windows (cf. Fig. 3). The heavy line drawn in the top two panels is that for Window 3. Panel a) includes the curves derived from using Windows 1 (thin full line and squares), 7 (dotted line and asterisks) and 10 (dashed line and triangles). Panel b) shows the results from using Windows 8 (thin full line and squares), 12 (dotted line and asterisks) and 15 (dashed line and triangles). Results for Vega have been omitted. Panel c) demonstrates how the scatter is reduced when the CP stars are also omitted (for reasons, see text), and enables the size of the scatter from those sources to be appreciated

For stars of types $\sim$ A3 and cooler, including those classified as Am, an F-type template appears to suffice for measuring RVs to a high accuracy (see Fig. 6), whereas for very early-A and late-B types a positive error of 0.2 - 0.4 kms^-1 may be incurred if an F-type template is used, and (more importantly) the accuracy achieved will depend fairly critically upon spectral peculiarity. It is therefore adviseable to establish for the hotter stars a linked sequence of templates for different spectral peculiarities.

We tested the validity of the above statements by replacing the 14 Del template with a synthetic solar-abundance spectrum calculated for $T_{\rm eff}$ = 9000, logg = 4.0 (i.e. no more than two subclasses removed from the spectrum of 14 Del), and broadened by a rotational velocity of 8 kms^-1. Cross-correlations were performed as for Fig. 9, for Windows 1, 3, and 7. In Fig. 10 we compare the results obtained with the synthetic and the 14 Del templates. The closeness of the comparison confirms the objectivity of all the results derived with the 14 Del template. Since the 14 Del results resemble those for templates at both extremes of the range, we infer that the precise spectral type of the template is not critical at all. When measuring the RVs of unknown programme stars, therefore, a guide as to their approximate spectral types would be helpful, but it is not necessary to classify the stars beforehand in any great detail.

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.synthetic.eps}}\\ \par\end{figure}$

Figure 10: Comparison of stellar and synthetic-spectrum templates for three different windows. The thick line depicts the results obtained by cross-correlating the test spectra against a synthetic noise-free spectrum calculated from a solar-abundance model with $T_{\rm eff}$ = 9000 K, logg = 4.0; the thin line refers to the results for the 14 Del template

A comparison of Figs. 5 and 9 clearly shows that the mismatch shifts between spectra which are closely adjacent in spectral type are dominated by the effects of individual differences other than those associated with a difference in $T_{\rm eff}$ . A procedure that is based primarily upon the criterion that the spectral types of the objects match as closely as possible a template from a grid of MK standards alone is therefore ineffective, but will be more rewarding if the grid is rich enough to include a diversity of spectral peculiarities (and provided that the vsini of all templates is sufficiently low). Since mismatch in intrinsic line profiles can give rise to larger RV shifts than does mismatch in spectral type, we conclude that - at least for the low rotational velocities represented by our sample - narrowness of line profiles should be regarded as a more important criterion in the choice of template than a close match in spectral type.

5.5 Unsuspected binary membership

HR 104 has a faint early-type companion (Hill et al. 1993). In Fig. 4 the large deviation of the thin line (no truncation) at (B-V) = 0.03 corresponding to HR 104 illustrates the strong disturbance to the CCF centroid that can be caused by even a faint companion spectrum if its velocity separation lies within a particular range. In order to examine more rigorously the conditions under which secondary spectra can or cannot be tolerated, we created two fake binary spectra. Each included a primary formed from one of two sub-sets of Sirius spectra; for the secondary, one binary incorporated the spectrum of the F5IV-V dwarf Procyon (Griffin 1979), while the other included the spectrum of Vega (A0 V). A grid of each type of binary was then generated, in which the secondary was reduced in magnitude relative to the primary by 7 values between $\Delta m$ = 1 and 5, and separated from it in RV by values ranging from 0 to 0.5 Å. Each resulting "binary'' was cross-correlated with the other subset of Sirius spectra. The results for Window 3 are illustrated in Figs. 11a and 11b. Figure 12 depicts in 3-D the effect of the Sirius-Procyon binary.

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.fakep.eps}}\\ (a) RV... ....fakev.eps}}\\ (b) RV shifts for a binary of Sirius + Vega \\ \par\end{figure}$

Figure 11: The influence of a faint companion upon the CCF (Window 3). An artificial binary was generated by adulterating the spectrum of Sirius with the spectrum of Procyon (upper plot), reduced by factors delta-m and displaced by 0.1 Å (full line), 0.3 Å (dotted line), 0.4 Å (dot-dashed line) and 0.5 Å (dashed line), respectively. The "binary'' was then cross-correlated against an independent spectrum of Sirius. The results for Window 1 gave slightly larger, but generally very similar, RV displacements. The lower panel shows the results of a similar test using Vega instead of Procyon as the secondary. (The model with 0.4 Å separation has been omitted for clarity)

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.3Dfake.eps}}\\ \par\end{figure}$

Figure 12: 3-D description of the influence of the "Procyon'' secondary in the fake binary. The maximum influence of this fairly narrow-lined secondary occurs near a separation of 30 pixels (0.3 Å). Beyond about 0.4 Å separation the secondary would scarcely affect the cross-correlation, however small the difference in magnitude, delta-m

These tests illustrate the non-negligible effects of even a faint ( $\Delta m >$ 4) secondary, and can be explained by considering the characteristics of the spectra forming the secondary in the fake binaries.

In our Procyon spectra the lines around $\lambda$ 4500Å have a FWHM of about 0.18 Å, and half-widths at the continuum of 0.25 to 0.3 Å; in our Sirius spectra the lines have a typical FWHM of about 0.375 Å. At zero RV separation between primary and secondary there is of course no disturbing influence upon the measured RV of the primary, but as a separation begins to grow it causes line asymmetries that deteriorate rapidly, giving rise to mis-match shifts that reach a maximum when the flanks of the secondary's lines reach just to the centre of the primary's lines (Figs. 11a and 12). Beyond that point, as the separation continues to increase the primary's contributions to the blends are less contaminated with the secondary's lines, so the mismatch shift decreases. At 0.5 Å separation enough of the cores of the primary's line-profiles are unaffected by the blending secondary that the mismatch shift falls to zero even with $\Delta m$ as small as 2, and the binary can be treated as a single-lined star.

The crucial factor is therefore the width of the lines in the secondary spectrum. In Vega the FWHM was measured on our spectra to be 0.55 Å, which explains why the disturbing influence of that secondary (Fig. 11b) persists when the binary is separated by 50 pixels (0.5 Å) even though the lines in Vega are weaker than those of Procyon and their overall influence is correspondingly smaller.

We conclude that a secondary spectrum can distort a measured CCF even if the companion star is too faint to be detected spectroscopically, and even if its temperature is fairly dissimilar from that of the primary; Sirius and Procyon are about 3000 K apart. The key factor seems to be not so much the actual temperature difference, as whether or not the secondary spectrum contains enough of the primary's spectral lines to produce a CCF signal from a template that matches the primary spectrum.

5.6 The usefulness of different windows

The windows defined in Table 2 were selected so as to include specific regions or groups of lines. It was expected that Windows 6 and 11 would only be suitable for a rather restricted range of spectral type. Thus Window 6, which contains the strong lines of FeI RMT 43, should have worked well for the cooler test stars but not the hotter ones, though in practice those Fe I lines are themselves asymmetrical and proved unsatisfactory for all types. Window 4, which isolates the Balmer lines, gave (not unexpectedly) broad CCFs and ragged results, and was only tried for contrast; it was not employed in any of the tests to measure RV shifts or errors. An additional window to include the SiI lines near $\lambda$ 3850Å was also tried, but was abandoned because that region is contaminated by other features in all but the hottest stars.

In general, the smaller the window the smaller the number of lines (i.e. signal), so the larger the random errors in the CCF. All of our observed spectra contain internal noise, though to differing degrees, and our experiments proved repeatedly that the tests decribed in Sect. 4 were best carried out with very wide span (Window 3), with supporting evidence where possible from Window 1 and subsets of Window 3 (chiefly Windows 7, 10 and 12). Window 12, which is a subset of Window 10, also tended to give results that were consistent (within a tolerance of 0.2 kms^-1) with those from Windows 1, 3 and 7, as did one of its sub-divisions (Window 15), though such a narrow window is prone to increased random errors. The other windows either contained features that tended to mask the underlying trends that we were measuring, or contained too few lines for robust results.

By examining the differential behaviour of the windows we were able to identify some of the blends that cause problems. Thus, while the behaviour of Window 12 was generally good, and that of Window 15 was also acceptable for the most part, the two other subsets, Windows 13 and 14, were noticeably bad. Here our conclusions differ slightly from those of Paper I, which found that its Windows 16-17, 17-18 and 18-19 (our Windows 13, 14 and 15, respectively) all returned low shifts for low $v_{\rm rot}$ . The problems with 13 and 14 stem largely from the strong FeII-TiII blends at $\lambda \lambda$ 4534 and 4549Å; both are somewhat temperature-dependent, the lower exciation potentials of the FeII lines being roughly twice those of the TiII lines. The blend at $\lambda$ 4534Å, a very unequal juxtaposition of two lines, is fully resolved when rotation is absent, whilst the feature at $\lambda$ 4549Å is a close blend of two fairly comparable lines of FeII and TiII plus a more distant line, and only the latter is fully resolved for zero rotation. Even though the amounts of rotational blurring present in many of our spectra are small, they are nevertheless sufficient to cause different mismatch shifts in the observed spectra of the individual stars when the components of the blends overlap by different amounts (see Sect. 5.5).

Window 12 also contains several lines of CrII which are enhanced in the Bp stars; CrII lines mostly occur in Window 15, but as they are not intrinsically blended there they do not give rise to a mismatch shift. Figure 13 illustrates the lines in Window 15 in different stars at about 9500 K. We note parenthetically that Window 15 occurs at the redward limit of our spectra where the signal was probably somewhat degraded, and unevenly so among the sample; in Sect. 6 we propose that further studies based on this region, with correctly optimized observations, should be particularly rewarding.

$\begin{figure} \resizebox{\hsize}{!}{\includegraphics{fig.4570.eps}}\\\par\be... ... 38 & 2.79 & 4596.060 & Fe I 820 & 3.59 \\ \hline \end{tabular}\par\end{figure}$

Figure 13: Spectra of o Peg, A1p (top), Sirius, A1m (centre) and 14 Del, A1V (bottom) in the region defining Window 15. The strongest lines are given ( NIST database; Moore 1945) as: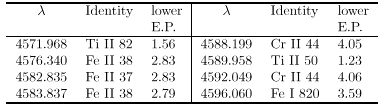

5.7 General conclusions

The overall results of this paper, now depicted in Fig. 9, are really quite surprising. Our cross-correlations sample a wide range of temperature (6500 < T < 12500), with the spectral type of the template (A1) near the median value. Enormous visible changes take place in spectral-line intensities across that range, and we would suspect that few lines were common and sufficiently unblended throughout. Yet it would appear that enough good-quality lines do persist between those two extremes to provide a basis for meaningful cross-correlation.

Our tests have also shown that large mismatch shifts can occur between any given pair of stars, whereas when one template is used to measure a range of spectral types a fairly smooth relationship is found, especially if extremes of spectral peculiarities and deviating line shapes are not included. We found moreover that the presence of natural broadening in the template, even as little as about 15 or 20 kms^-1, gives rise to a trend in RV shifts that demonstrates how rotation can aggravate the effects of spectral-type mismatch, and in addition we showed that any attempt to effect rotational matching by artificially broadening either object or template can seriously exacerbate existing slight differences in intrinsic shapes of lines and blends, and can magnify an RV error that need not be apparent if the spectra are cross-correlated in the natural state.

The use of real spectra for these experiments has thus provided some interesting and decisive results that complement the theoretical studies, especially since we could differentiate visually between profiles broadened by stellar rotation, and profiles that are broadened by a star's characteristic surface velocity fields, or "microturbulence''. The scope of the conclusions has however been limited by the S/N ratio of the observations and by the number and variety of stars in the sample. The need for high resolution in these tests has also been affirmed, particularly from our experiences with the spectra of Sirius and Vega; with coarser sampling it might not have become apparent that such modest rotational broadening does have an appreciable effect at the level of accuracy for which we are aiming, nor that line profiles could be so strikingly non-Gaussian.

The spectrum mismatch shifts depicted by the heavy line in Fig. 9 occur very largely because line blends in stellar spectra are composed of features whose relative strengths differ, principally through $T_{\rm eff}$ , logg or chemical composition. Rotational broadening, whether present in the object or the template or both, will clearly tend to exacerbate that situation. Were all the lines in a stellar spectrum sufficiently isolated, none of those errors would arise. Our selection of different windows helped to identify some of the more prominent lines or blends e.g. of FeII and TiII at $\lambda$ 4534 and 4549Å, which are responsible for the observed mismatch shifts.

Where the dominant factor in spectrum mismatch is the difference in temperature and not chemical peculiarity, we have been able to confirm, for all but the hottest samples, the magnitude of the mismatch shifts ( $\Delta$ RV $\approx$ 0.05 kms^-1) derived in Paper I for synthetic, noise-free solar-abundance spectra. However, inasmuch as mismatch shifts are also caused by intrinsic differences between spectra of similar $T_{\rm eff}$ but different chemical composition, the results of the present paper complement those of Paper I. For reasons already given, our sample contained several spectroscopically "abnormal'' stars, there being little actual choice of "normality'' owing to our insistence upon the sample being restricted to narrow-lined spectra. (The description "normal'' has confusing connotations for B and A types, where the seemingly high frequency and disparity of chemical peculiarities, together with a possible bias through observational selection and high binary incidence (Ramella et al. 1989), calls into question the definition of a norm). We have shown that spectral peculiarities among stars of types late B to mid A are more deleterious in causing RV shifts than are differences in temperature between spectral sub-classes. However, since the occurrence of a foreign feature in the test spectrum close to a line that is common to both test and template is random, albeit shared to some extent by stars showing generically the same peculiarity, chemical abnormalities chiefly cause scatter on the mismatch curve.

To identify the effects of spectral-type mismatch (to within the noise limitations of our data), we eliminated from Fig. 9 the 4 stars classified as CP (HR 7664, $\phi$ Her, $\beta^2$ Cap and o Peg) - see Fig. 9c. We also eliminated Vega because its lines have profiles that appear sufficiently unusual (see Sect. 2.2) to cause particularly deleterious mismatch, but retained the metallic-lined stars since their abundance peculiarities are chiefly represented by an overall strengthening of metallic lines. The curve in Fig. 9c has much less noise than those in Figs. 9a and b, and indicates how much of the small-scale scatter in the upper parts of those and similar figures is attributable to chemical peculiarities. Figure 5, on the other hand, is not substantially changed by eliminating the CP stars.

Similarly to what we found in Paper I for spectra with high rotational velocities, the results from the reduced sample suggest that for slow rotators too the RV displacements caused by spectrum mismatch are not as random as might be supposed intuitively (or as Fig. 5 might be thought to indicate). Even across a span of more than 800 Å the mismatch shift for the hotter stars is systematic. The tendency of mismatch curves to turn upwards towards the earlier types (see Fig. 9c) reflects a correlation between the temperature of the hotter objects and the mismatch shift, if a fixed template is used. We note that Morse et al. (1991) also found the same positive correlation of shift with $\Delta$ $T_{\rm eff}$ for $T > 9\,000$ (the lower limit of their study). We have also shown that the gradient towards decreasing (B-V) is independent of the spectral type of the template (Fig. 6).

There is a general trend towards smaller mismatch shifts at the cooler end of the sample even when the template's lines are broader than those of the test spectra (Figs. 3, 8). While it is true that the cool stars in our sample do not include such striking chemical peculiarities as occur among the hot ones, the chief reason for that trend is (we suggest) an increasing tendency for mismatch shifts arising from individual blends or groups of blends to cancel statistically with increasing lateness of type as the density of lines grows. Microturbulence may also tend to increase with cooler A types (Landstreet 1998), slightly counteracting the benefits of an increasing line density; however, its links to the structure of the convective movements in a stellar atmosphere imply a dependence upon spectrum peculiarities and hence wide individual deviations from the norm, and it will require a much larger sample of spectra than ours to support a quantitative differentiation between its effects. At present we can simply give the opinion that, in most applications, the total RV error will best be contained by choosing a template with the narrowest possible lines, and disregarding any "rotational mismatch" between object and template.

We have shown that it will be possible to measure RVs to an accuracy considerably better than 1 kms^-1 for slowly rotating stars in the temperature range examined, provided certain criteria are met in the selection of the template spectrum. In view of the large range of spectral idiosyncrasies that occur beween mid-B and early-A types, a choice of stellar templates is likely to prove more reliable than a grid of synthetic spectra which is not able to include either the diverse spectral peculiarities of CP stars or a good detailed representation of stellar velocity fields. In choosing a stellar template to minimize systematic mismatch shifts, the principal criterion is for as little rotation as possible. The other criteria specify that the spectra need to be of sufficiently high S/N ratio that random errors are contained, and (obviously) as free as possible themselves from internal systematic errors (e.g. in wavelength scales). For many applications the cross-correlation should use a window of maximum width. Figure 9 shows that the mismatch curve may exhibit considerably more scatter when a small-span window is used in cross-correlating real spectra, though in the next section we comment on the potential of using a small window in the case when it does not contain any harmful blends and when random errors are controlled by employing very high S/N. We must however point out that the above results have been reached through studies of quiescent dwarf stars, and may therefore only be applicable to those and similar stars.

5 Interpreting the measured RV shifts

5.1 Are the Sirius results representative?