In this section we describe the generation of wavelength-calibrated spectra from the observations, and discuss aspects of their derivation which impinge upon the accuracy and precision of their wavelength scales.

The observed spectra to be used in these experiments must have wavelength scales that are more accurate (i.e. have smaller systematic errors) than the likely mismatch errors that we propose to investigate. However, the extraction of spectra from observations can introduce extraneous errors of technical (instrumental and processing) origin. We therefore focus first on those sources, and describe our attempts to minimize, if not altogether eliminate, the attendant errors. We address the question of absolute stellar RVs here, also. We aim to reduce all controllable errors in these spectra to less than 0.1 or 0.2 kms^-1 (< 3 mÅ at $\lambda$ 4200Å).

In order to satisfy the project's demands for variety and wealth of spectroscopic features (which in early-type stars implies a wide wavelength range), we require a large, homogeneous set of high-resolution, high-S/Nspectra representing a broad selection of early-type stars, all with accurately-known absolute velocities. The greater the resolution, the better our ability to investigate the effects of blends, provided $v_{\rm rot}$ is also small; a resolving power of 10⁵ has the same blurring effect as $v_{\rm rot}$ = 3 kms^-1. If practical considerations dictate that the spectra have to be observed with different equipment, modes must be selected that are as similar as possible to one another so as to reduce any systematic effects due to differences in resolution, spectral definition or wavelength range; whenever spectral characteristics are not fully shared between object and template, the likelihood of distorting the symmetry or position of the CCF, i.e. of adding systematic error to the RV, is increased.

Despite nominal similarities in resolving power, different spectrographs possess different characteristics of instrumental profile (point-spread function), spectral definition, and fiducial wavelength source ("arc" spectra). If the lines being cross-correlated are isolated and symmetrical and instrumental profiles are symmetrical, small differences in resolution or definition are not expected to contribute errors that are significant for this project. Problems arise when spectral lines are blended, particularly if they are of unequal strength, because the degree of blending will depend both upon instrumental resolution and upon the extent of the wings of the instrumental profile. Moreover, some differential behaviour of those properties with wavelength can be expected since the design of the optical components in the spectrograph will have been optimized optically for a particular wavelength.

The foregoing refers, of course, to the intrinsic properties of a spectrograph, and excludes spectral degradation caused by incorrect focus or spectrum tilt.

3.2 Observational material

Owing to various constraints of time, resources and equipment we have depended upon archived photographic spectra for this project. The wide wavelength coverage and fine pixel size that are characteristic of many photographic spectra (e.g. Griffin 1968; Griffin 1979) render the latter particularly suitable as test material. High S/N can be achieved by co-adding multiple spectra. We chose a wavelength region of $\sim 1\,000$ Å between the Balmer discontinuity and H $\beta$ .

The quantity of such data is in principle vast; in practice, lack of ready access to many plate stores restricted the choice substantially. To minimise the dangers discussed above, we selected spectra mostly from two sources: the Dominion Astrophysical Observatory (DAO) and Calar Alto (CA), and from two specific instrumental combinations: the 96-inch camera and mosaic grating (830 lines mm^-1) of the DAO 1.2-m, and the f/12 camera and 632 line mm^-1grating of the CA 2.2-m telescope. Both spectrographs offer a maximum reciprocal dispersion near 2.3 Åmm^-1 in the blue, and in both cases two 10-inch plates are placed end-to-end in the plate holder, thereby admitting a small gap at the exposure centre. Other relevant characteristics are substantially different, however. Intensity calibrations at the DAO are exposed directly onto the plate, whereas at CA one must employ an auxiliary system; at the DAO the relatively small telescope aperture is compensated by an image slicer whose fixed area limits the attainable S/N of a photographic exposure, whereas at CA the conventional entrance slit can be widened to 2.7 mm, and even to twice that, if feasible.

Table 1: Selected spectra
Star HR Spectral (B-V) $T_{\rm eff}$ $^{\dagger}$ vsin $i^{\S}$ Source No. of S/N Wavelength Remarks

type^* spectra range

64 Ori 2130 B8 III/V -0.11 12000 5 DAO 1 50 3750-4600 SB2

8094 B9 V -0.10 11700 12 DAO 1 30 3750-4600 SB

7664 B9p -0.08 11100 9 DAO 11 140 3750-4600 SB HgMn

$\phi$ Her 6023 B9p -0.07 10850 10 CA 2 50 3750-4418 SB HgMn

21 Peg 8404 B9.5 V -0.07 10850 5 (3.9) DAO 1 30 3750-4600

$\beta^2$ Cap 7775 B9.5 -0.02 9850 4 DAO 1 40 3750-4600 SB Hg Mn

o Peg 8641 A1p -0.02 9850 8 DAO 13 150 3750-4600 SB HgMn

Vega 7001 A0 V 0.00 9550 25 MW 9 $^{\P}$ 300 3750-4600 Unusual line profiles

$\gamma$ Gem 2421 A0 IV 0.00 9550 12 (11.3) CA 2 70 3750-4317 SB

Sirius 2491 A1 V 0.01 9400 17 (16.5) MW 10 $^{\P}$ 300 3750-4600 A1m (mild)

14 Del 7974 A1 V 0.02 9250 6 DAO 1 40 3750-4600 SB

104 A2 V 0.03 9150 6 DAO 3 70 3750-4600 Very faint secondary

60 Leo 4300 A1m 0.05 8900 14 CA 1 60 3750-4453

95 Leo 4564 A3 V 0.11 8350 8 CA 1 30 3750-4600 SB2

32 Aqr 8410 A5m 0.23 7600 12 (1.0:) DAO 8 80 3750-4600 SB

$\iota$ Psc 8969 F7 V 0.51 6250 8 DAO 3 70 3750-4600

**Table 1:** Selected spectra
Star	HR	Spectral	(B-V)	$T_{\rm eff}$ $^{\dagger}$	vsin $i^{\S}$	Source	No. of	S/N	Wavelength	Remarks
		type^*					spectra		range
64 Ori	2130	B8 III/V	-0.11	12000	5	DAO	1	50	3750-4600	SB2
	8094	B9 V	-0.10	11700	12	DAO	1	30	3750-4600	SB
	7664	B9p	-0.08	11100	9	DAO	11	140	3750-4600	SB HgMn
$\phi$ Her	6023	B9p	-0.07	10850	10	CA	2	50	3750-4418	SB HgMn
21 Peg	8404	B9.5 V	-0.07	10850	5 (3.9)	DAO	1	30	3750-4600
$\beta^2$ Cap	7775	B9.5	-0.02	9850	4	DAO	1	40	3750-4600	SB Hg Mn
o Peg	8641	A1p	-0.02	9850	8	DAO	13	150	3750-4600	SB HgMn
Vega	7001	A0 V	0.00	9550	25	MW	9 $^{\P}$	300	3750-4600	Unusual line profiles
$\gamma$ Gem	2421	A0 IV	0.00	9550	12 (11.3)	CA	2	70	3750-4317	SB
Sirius	2491	A1 V	0.01	9400	17 (16.5)	MW	10 $^{\P}$	300	3750-4600	A1m (mild)
14 Del	7974	A1 V	0.02	9250	6	DAO	1	40	3750-4600	SB
	104	A2 V	0.03	9150	6	DAO	3	70	3750-4600	Very faint secondary
60 Leo	4300	A1m	0.05	8900	14	CA	1	60	3750-4453
95 Leo	4564	A3 V	0.11	8350	8	CA	1	30	3750-4600	SB2
32 Aqr	8410	A5m	0.23	7600	12 (1.0:)	DAO	8	80	3750-4600	SB
$\iota$ Psc	8969	F7 V	0.51	6250	8	DAO	3	70	3750-4600

^*Source: Bright Star Catalogue (Hoffleit 1982).

$^{\dagger}$ $T_{\rm eff}$ merely corresponds to a calibration of (B-V) (see text).

$^{\S}$ Values in parentheses are for rotation alone (Landstreet 1998), whereas our measurements include microturbulence.

$^{\P}$ Individual exposures cover no more than half of the full span used in the project.

We also used some very high-dispersion spectra (down to 0.75 Åmm^-1) of Sirius and Vega taken on IIIa-J emulsion with the Mount Wilson (MW) 100-inch telescope and coudé spectrograph, and intended as material for a spectrophotometric atlas (in preparation). For those spectra the 3 $^{\rm rd}$ or 4 $^{\rm th}$ orders of the 133B grating (900 linesmm^-1) and 114-inch camera had been used. The grain size of the IIIa-J emulsion is almost 3 times smaller than that of the IIa-O emulsion employed at the DAO and CA.

One disadvantage of using archived spectra is an inevitable sacrifice of homogeneity. Fortunately, however, the diversity of the material - dictated by the differing original purposes for which the observations were made - was tolerable. The DAO archive contains the fruits of several programmes designed to study chemical abundances in sharp-lined Bp, Ap and Am types or to monitor RVs of binaries, and includes several fairly homogeneous sub-sets of sharp-lined spectra. The CA archive is much less extensive; we used a number of high-dispersion spectra of late-B and early-A stars taken by REMG for a programme whose objective was to push the spectral coverage deep into the photographic UV. Few of those plates have the same wavelength coverage.

The selected observations, listed in Table 1, comprise the test spectra which we will cross-correlate in pairs in order to investigate the effects of spectrum mismatch. For each star, the table gives its listed spectral type, source of observation(s) and number of exposures used, its measured (B-V), a suggested temperature derived from its (B-V) (Flower 1996), the S/Nratio, and our estimates of vsini. Note that the values of $T_{\rm eff}$ given in the Table are not spectroscopic derivations, and should not be treated as such. S/N ratios were determined from the noise levels in selected regions of continuum; the values are closely related to the total spectrum width (perpendicular to the dispersion) and inversly to the grain size of the emulsion used. All spectra were of high resolution; the DAO instrumental profile, for instance, measured as 75 mÅ at 4500Å from the FWHM of arc lines (in good agreement with the value of 73 mÅ determined by Booth et al. 1990 for the same equipment), is equivalent to an instrumental broadening of 2.5 kms^-1. Projected rotational velocities could therefore be determined empirically by broadening the arc lines to make them match the widths of the stellar lines. Our measurements agree well with those of Landstreet (1998), except for 32 Aqr. However, Landstreet segregated rotation and microturbulence whereas our values refer to the combined broadening. For 32 Aqr, he gives a microturbulence of 4.5 kms^-1. Each DAO spectrum covered the full extent of 850 Å (3750-4600Å) used in this paper. The MW spectra were randomly centred since each included only 400-500 Å at higher dispersion, so were pieced together to cover the same wavelength range as the DAO spectra. Most of the CA observations were centred at shorter wavelengths than the mid- $\lambda$ of the DAO spectra; as a result our spectra of $\phi$ Her, $\gamma$ Gem and 60 Leo do not quite cover the full wavelength range used in these experiments.

The rest of this section describes the steps taken to generate accurate wavelength scales for these spectra.

3.3 Digital microphotometry

The DAO plates were traced with the DAO's modified PDS scanner (Stilburn et al. 1992). Most of the Calar Alto plates and all of the MW plates were traced with the PDS at the Royal Greenwich Observatory, Cambridge; a few were scanned at the DAO. The two machines offered a different range of set-up parameters. We used a slit-aperture of 8.5 $\times$ 350 $\mu$ m at the DAO, and 10 $\times$ 200 $\mu$ m at Cambridge; the output was recorded in steps of 6.01 $\mu$ m at the DAO, or 5.0 $\mu$ m at Cambridge. Since neither scanner provided an entrance slit that could accommodate the full height of our spectra, both had to be used in raster mode. "Clear plate'' was traced as closely as possible to the stellar spectrum and with the same effective slit aperture, but with a sampling frequency of 1/20, i.e. in steps of 120.2 $\mu$ m at the DAO, or 100 $\mu$ m in Cambridge. Arc spectra were traced with the same step-size and slit-width as for the stellar spectra, but with the number of rasters adjusted as appropriate. The DAO scans were recorded as FITS files and were read with IRAF; the Cambridge scans were recorded in a local format. Both sets were reduced with purpose-designed software.

Direct-intensity calibration exposures consisted of (a) a sequence of contiguous strips recorded on the star plate at the DAO, (b) two sets of individually separated strips, also recorded directly, on the MW plates, or (c) a set of individually separated strips in random order observed with an auxiliary spectrograph for the Calar Alto plates. The calibration equipment and procedures at the DAO are described in detail by Richardson (1968), whilst those of MW, including the auxiliary calibration equipment also used at CA, are given by Griffin (1979). The calibration strips were also traced in rasters, mostly at intervals of 200 Å(100 Å very occasionally), to yield the respective characteristic (H&D) curves (Hurter & Driffield 1890). The plate transmission measurements, normalized to the local, smoothed "clear plate'', were converted into direct intensities by applying, at every point, the calibration relation that was nearest to it in wavelength. An extracted spectrum thus consisted of regularly-spaced intensity values recorded in the direction of the dispersion.

3.4 The problem of absolute stellar radial velocities

A cross-correlation between two observed spectra will include the difference between the actual (intrinsic) stellar velocities, together with systematic errors due to mismatch and errors stemming from processing the spectra. Clearly, the assessment of mismatch errors can only commence if the intrinsic RV difference is known and the processing errors are contained. Unfortunately, few of the wide selection of stars needed for this project have known RVs that meet our needs in terms of accuracy and precision. Early-type stars with sharp lines are often suspected of belonging to binaries, but it cannot be determined to the same degree of certainty whether those rotating more quickly are not also binary members. Sharp-lined CP stars also manifest line-blending with periods of a few days which is ascribed to spots that traverse the visible disk as the star rotates. Seeking accurate values of constant velocity for many of those stars may be impractical, even meaningless.

We circumnavigate the problem by determining a wavelength scale for each observed spectrum within the velocity frame of the star itself, thus making available very many more early-type stars for this project. The accuracy with which such a wavelength scale can be determined depends chiefly upon the density of the selected lines and their intrinsic widths, but also upon their intrinsic shapes. Single-lined spectroscopic binaries can thus be included in this study without requiring any knowledge of their orbital periods; even dominant primary components in double-lined systems can be used if necessary, with care. Our cross-correlation tests will therefore simply look for CCF displacements that differ from zero. But the level of accuracy achieved will depend critically upon how accurately the wavelength scales have been generated.

3.5 Deriving accurate "stellar'' wavelength scales

The technique we adopt is to assign rest-wavelengths to unblended stellar lines whose relative positions are measured accurately, and to apply the grating equation to solve for the parameters describing the spectral dispersion. The calculated wavelength scale is thus anchored to the rest-wavelengths of the star. The technique was described in the Introduction to the Procyon Atlas (Griffin 1979), and those authors have in fact long adopted it as routine. For stellar abundance work, where the stellar RV may not be required, it avoids the need to correct measured wavelengths for purposes of line identification. It also avoids the introduction of errors between the reference source ("arc") and the stellar spectrum; a discussion of the sources of those errors is given by Griffin (1973).

According to the grating equation, each point at wavelength $\lambda$ on the focal plane obeys the relationship

where n is the grating order (n = 2 for the DAO and CA spectra described here, 3 or 4 for the MW spectra), d is the grating constant and $\alpha$ is the angle between the incident light and the normal to the grating. $\beta$ , the angle of refraction, involves the camera focal length Fand the measured position D of each point. Positions are measured relatively, so $\beta$ includes a constant representing the origin of the measurements.

We measure the positions of the identified lines by cross-correlating the raw spectrum with a symmetrical, empirical profile that resembles the stellar line profiles, and select wavelengths from a homogeneous, high-quality source. The numbers of identified lines will vary widely (from $\sim$ 100 downwards per span of 400 Å), depending upon the nature of the spectrum; however, it is important that they be well distributed in wavelength. Values of F and $\alpha$ , which are coupled, are derived iteratively by least-squares solution, and the resulting spectra are re-binned into the required step-size.

Each derivation of F and $\alpha$ will be affected by random errors in Dand in the quoted wavelengths, by asymmetries (whether of instrumental or astrophysical origin) present in the spectrum lines, and possibly by systematic errors (e.g. thermal drifts) in the PDS; however, the latter are normally found to be negligible. Incorrect camera focus and tilt can be a significant source of instrumental asymmetry; the shapes and locations of extra- and intra-focal images differ, as is readily appreciated when examining focus tests on emission lines, and even the best focus setting will be a compromise to cope with the simultaneous existence of extra-focal asymmetries, plate-tilt errors, and irregularities in the plate-holder.

3.6 The usefulness of comparison arc spectra

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.w16.eps}}\par\end{figure}$

Figure 1: Residuals, in mÅ, for arc lines (asterisks) and stellar lines (circles) on one half of a DAO exposure, after solving and correcting for the stellar radial velocity. The solution derived from arc + star combined has $\alpha$ = 25.510, $F = 243.25148 \pm 0.00061$ cm, and an rms deviation of $\pm$ 3.31 mÅ for the 49 stellar lines and $\pm$ 1.69 mÅ for the 38 arc lines (0.23 and 0.12 kms^-1, respectively, at the median wavelength). The derived topocentric radial velocity was 19.723 kms^-1 $\pm$ 0.037 kms^-1

The derivation of a star's radial velocity by the classical method of measuring its spectrum against a fiducial one (a laboratory spectrum) can produce low formal errors under favourable conditions. In our application of the method (see Fig. 1), F and $\alpha$ are first derived separately from the arc lines and from the stellar lines; the RV is then the shift required to merge the two sets and is determined iteratively, making adjustments to F and $\alpha$ so as to minimize the overall residuals. The rms deviation in Fig. 1 is 0.23 kms^-1 at the median wavelength for the 49 stellar lines and 0.12 kms^-1 for the 38 arc lines, with formal errors of 0.03 kms^-1 and 0.02 kms^-1, respectively, while the formal precision of the measured RV difference between them was 0.037 kms^-1. However, those levels of precision are misleading, as we now show.

The method outlined in Sect. 3.5 obviates the need for a fiducial wavelength reference. Nevertheless, because arc lines are always more narrow, and usually more numerous, than stellar lines in early-type spectra, F and $\alpha$ for a given exposure can in principle be derived with higher precision from arc lines. We therefore applied the grating equation to the Fe-Ar arc spectra on the DAO exposures, measuring the positions of all unblended low- and medium-strength lines by cross-correlation with a matching, symmetrical emission profile, and adopting Ar I, Ar II, Fe I and Fe II wavelengths from the NIST database (http://physics.nist.gov/cgi-bin/AtData/main_asd). Measurements of the arc spectra on either side of a star spectrum were averaged. The pairs of data points (wavelength, position) constituted a set of simultaneous equations whose solution yielded least-squares values for $\alpha$ and F.

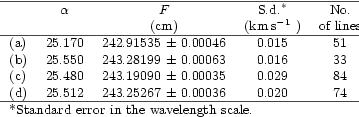Figures 2a and 2b show typical optimized solutions for the separate halves of a DAO exposure; the rms scatter of the points around zero, in kms^-1 at the median wavelength, is recorded in the caption. Lines near the extreme short- and long-wavelength ends were not used as they tend to be distorted through vignetting in the spectrograph. Lines within at least 1 cm of the plate join were also rejected; as a wet photographic emulsion dries it does so at the edges first, causing slight stretching and distortion there and producing wavelength residuals close to the plate join (positive for the short-wavelength half of an exposure, negative for the other) that are several times larger than the expected accidental errors.

As the caption to Fig. 2 indicates, the two halves of the same plate do not yield the same solution, and the differences are well outside the respective error bars. Accordingly, when the two halves are brought together (Fig. 2c), the solution can only force a compromise that suits neither half as well as do the individual solutions. The two curves in Fig. 2c are actually part of the same curve, but because the measurements of line positions were not continuous across the plate join the wavelength solution has been able to introduce an arbitrary shift between the two halves in an effort to minimise the overall errors. All the arc spectra behaved in a similar fashion, apart from random errors of measurement. The same effect was also visible (though with increased noise) in the individual arc exposures above or below the star exposure.

We have not yet found a satisfactory explanation as to why the physically separate halves of an exposure should consistently give distinctly different sets of scaling parameters ( $\alpha, F$ ). Possible causes include misalignment in the arc, image-slicer or camera (its focus or tilt), the collimation of the spectrograph, optical vignetting, errors in the figure of the camera mirror or in the plate-holder, or an error of runs in the grating. The pattern of residuals from the DAO spectra maintained a similar amplitude regardless of the epoch or the observer; it therefore seems unlikely that the cause lay in a single maladjustment (such as camera focus) over which the observer has control, though camera tilt is less industriously investigated, and spectrograph collimation is not often altered. A similar effect was also found, in a separate investigation, in arc spectra on plates from both Calar Alto and Mount Wilson. At CA the effect was less pronounced, while at MW it was similar in magnitude to that at the DAO but in the reverse sense. At the DAO and CA the grating is used almost normal to the incident beam whereas at MW it is used at a substantial angle of incidence, so indeterminacy in the grating equation is not thought to be a cause. In our investigation of the stellar spectra themselves (Sect. 3.7), where random noise was sufficiently small we found indications of the same anomaly but smaller in amplitude, and in one case of particularly sharp stellar lines it was not present at all (Fig. 2d). The formal error for the stellar lines in that example is only 1.5 times the values derived for the half-sets of arc lines in Figs. 2a or 2b. But the optimal solution of 25.512 for $\alpha$ differs significantly from the 25.480 derived from the arc lines (Fig. 2c); imposing one value upon the other solution gives unacceptably bowed residuals. We can summarize the situation by stating that, for stellar spectra, the systematic errors in the residuals tend to be smaller than the random errors, whereas the reverse is true for arc spectra.

We recall that we only proposed the use of arc spectra here in the expectation of improving the precision in our stellar wavelength scales. Clearly we cannot rely upon arc spectra for that purpose to the level of accuracy required, though we can estimate an uncertainty of $\sim$ 1.5 mÅ (0.1 kms^-1) arising from our procedure (as opposed to other internal errors, Sect. 4.2.2), with the formal error of 0.02 kms^-1 as the lower limit. The findings have actually raised more questions than they answered, not all of which are directly relevant to the tasks set by our project, and merit a study of their own. The search for the cause(s) of the anomalous behaviour in arc spectra would benefit from studies of other wavelength regions and other spectrographs, and could make use of archived spectra. Unfortunately, few of the sharp-lined stellar spectra from CA and MW which we used in this study included suitable arc exposures.

3.7 Wavelength scales for our test spectra

We determined wavelength scales directly for the stellar spectra. Positions of identified stellar lines were measured on each exposure by cross-correlation with a matching, symmetrical absorption profile, and least-squares values for $\alpha$ and F were derived, as above. Stellar wavelengths were taken from the solar tables by Pierce & Breckinridge (1973), where the estimated total error (systematic + random) in the blue region is given as $\pm$ 3 mÅ. Given the experience of Sect. 3.6, we decided to treat each half of a stellar exposure independently. The solutions did not include high-order terms (i.e. no curvature of the residuals). Since many of the DAO spectra had been obtained in homogeneous series, the values of ( $\alpha$ , F) derived for the sharp-lined stars were helpful in constraining the solutions for spectra with less sharp lines (i.e. with intrinsically higher random errors).

We attempted to optimize the wavelength solutions by considering the residuals from the same lines measured in different spectra. Some lines gave unacceptably poor residuals, either because of random errors in the stellar measurements or the solar wavelengths - many lines in A-type stars are very weak in the solar spectrum - or because of unsuspected blending, and were rejected. Lines were also rejected from individual plate solutions if the residuals were greater than 10 mÅ, and were not used at all if they proved to be bad in more than half of the samples in cases of multiple exposures. We then examined the three spectra for which we had multiple homogeneous exposures (13 of o Peg, 11 of HR 7664, 8 of 32 Aqr), and determined for each star the straight mean of the wavelengths calculated for each individual line, normalizing the means so as to eliminate an overall shift. With little variation, the adjustments to the formal wavelengths were similar in sign and size in all three stars. We then adopted these adjusted wavelengths as our new reference ones for all the spectra and repeated the wavelength solutions, extracting spectra in steps of 10 mÅ. The spectra were finally normalized in intensity by placing the continuum at 100%.

Each DAO spectrum was extracted in two intervals, $\lambda 3750-4150$ Å and $\lambda 4200-4600$ Å, conjoined with a 50-Å blank continuum; we thus avoided the troublesome plate joins, and also accommodated small differences in the precise centering of the different exposures. The CA and MW spectra were also extracted within the same overall interval, as far as the extent of each individual observation permitted.