Since an RV shift is linear in log $\lambda$ , we re-binned each spectrum in uniform steps of log $\lambda$ , choosing a step size $\Delta$ (log $\lambda)$ = 2.3 10^-6 as a reasonable compromise to match both the spacing (10 mÅ) and the number of points (mostly 85000) in the original spectra. One bin thus corresponds to 0.75 kms^-1. Since mismatch shifts may depend on a great variety of factors, both astrophysical (see Sect. 2) and related to the technical details of an RV measurement (e.g. the choice of a suitable spectral "window'' to be used), the first step in our strategy to study those shifts was to choose one spectrum (of high S/N ratio, to reduce random errors) as a reference template and to cross-correlate all the other spectra in turn against it. The obvious choice for this reference was the Sirius spectrum because of its high quality (see Table 1), and because its temperature is more or less at the median of the range covered by our sample. Vega, also of high quality, seemed less suitable because its lines are somewhat weaker and have unusual profiles. At a later stage we also used other spectra as a common template and investigated the mismatch shifts which occur when (as in Paper I) the temperature difference between template and object was kept to a minimum.

A cross-correlation measurement extended across 161 bins, yielding a smooth curve ( CCF) whose centroid was the required RV measurement. Anticipating that the CCF might not be symmetrical (frequently it was not), we generated the mirror image of each cross-correlation and superimposed the pairs graphically, allowing the fit to be modified manually. For symmetrical CCFs the position of the centroid was judged from the central section, which was normally not more than 40 bins wide, though in cases of asymmetry we considered only the central region of that.

We recall at this point that, in the absence of spectrum mismatch, the only expected deviations of a CCF's centroid position from zero will be caused by random or systematic errors originating in the processes of observation, data reduction and shift measurement; we refer to those errors as internal errors, as distinct from possible bias originating elsewhere. We also remark that any shifts due to spectrum mismatch, though formally "systematic errors'' in the framework of an RV measurement, are not regarded as errors per se in the present study.

The main results from cross-correlating the test spectra against Sirius are summarized in Fig. 3, which illustrates the dependence of the mismatch shifts on temperature. To achieve those results we followed a specific set of procedures, though only after various iterations since it was necessary first to recognise, control and as far as possible quantify the factors other than strict spectrum mismatch which could contribute their own RV shifts.

$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.sirius.eps}}\par\end{figure}$

Figure 3: Measured RV shifts, in kms^-1, resulting from cross-correlating test spectra against Sirius. The abscissa is the (B-V) of the test star. The heavy line drawn in both panels refers to Window 3. The upper panel compares the curves derived from using Windows 1 (thin full line and squares), 7 (dotted line and asterisks) and 10 (dashed line and triangles). The lower panel compares the results from using Windows 8 (thin full line and squares), 12 (dotted line and asterisks) and 15 (dashed line and triangles)

The interpretation of those results, with a discussion of the different effects of diverse kinds of spectrum mismatch, is presented in Sect. 5. In the present section we discuss the procedures adopted: the selection of spectrum "windows'' of various widths and purposes (Sect. 4.1.1), and why we truncated the spectra at 95% of the continuum level (Sect. 4.1.2). We also conduct tests on sub-sets of spectra in order to examine the internal errors (see Sect. 4.2), and describe other possible sources of error that might affect the results (Sect. 4.3).

4.1.1 Window selection

As in Paper I, we selected "windows'' to restrict the wavelength range of the cross-correlation, though here we included only three of Paper I's windows (Nos. 16-17, 17-18 and 18-19). Somewhat in contrast to Paper I, which employed window widths all around 30Å (except for those containing a Balmer line), we have chosen windows with a variety of widths, ranging from the total useable range of 850Å down to only 14Å. One purpose was to study the effects of isolating or excluding different groups of astrophysically-significant features such as the Balmer lines (Window 4), the CaII K line (Window 5), lines of FeI RMT 43 (Moore 1945) in Window 6 ( $\lambda$ 4063Å is a temperature-dependent blend of two FeI lines of different excitation potential), and other temperature-dependent blends, e.g. FeII and TiII at $\lambda$ 4534 and 4549Å (Windows 13 and 14). The wavelength limits of the windows are listed in Table 2. Care was taken to ensure that the end wavelengths occurred in continuum regions for all the spectral types considered. For that reason the first 32Å of spectrum could not be included in Windows 1 and 4.

Table 2: Windows for the cross-correlations
no. Start $\lambda$ End $\lambda$ Span Comment

(Å) (Å) (Å)

1 3782 4600 818 Full span

2 3811 4600 789 Balmer lines omitted

3 3811 4600 789 No Balmer lines or K line

4 3782 4127 345 Balmer lines only (5)

5 3924 3940 16 K line only

6 4038 4073 35 Fe I, RMT 43

7 4141 4292 151 All lines between H $\gamma$ & H $\delta$

8 4230 4265 35 sub-set of Window 7

9 4265 4282 17 sub-set of Window 7

10 4382 4600 218 Longward of H $\gamma$

11 4406 4420 14 Prominent lines at early A

12 4500 4600 100

13 4510 4537 27 Window 16-17 of Paper I

14 4537 4570 33 Window 17-18 of Paper I

15 4570 4600 30 Window 18-19 of Paper I

**Table 2:** Windows for the cross-correlations
no.	Start $\lambda$	End $\lambda$	Span	Comment
	(Å)	(Å)	(Å)
1	3782	4600	818	Full span
2	3811	4600	789	Balmer lines omitted
3	3811	4600	789	No Balmer lines or K line
4	3782	4127	345	Balmer lines only (5)
5	3924	3940	16	K line only
6	4038	4073	35	Fe I, RMT 43
7	4141	4292	151	All lines between H $\gamma$ & H $\delta$
8	4230	4265	35	sub-set of Window 7
9	4265	4282	17	sub-set of Window 7
10	4382	4600	218	Longward of H $\gamma$
11	4406	4420	14	Prominent lines at early A
12	4500	4600	100
13	4510	4537	27	Window 16-17 of Paper I
14	4537	4570	33	Window 17-18 of Paper I
15	4570	4600	30	Window 18-19 of Paper I

4.1.2 Should the spectra be truncated?

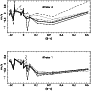$\begin{figure} \par\resizebox{8cm}{!}{\includegraphics{fig.trunc.eps}}\par\end{figure}$

Figure 4: RV shifts measured by cross-correlating test spectra against Sirius when the test spectra have been truncated at different percentages of the continuum. Heavy line: 95% truncation (the same heavy line as in Fig. 3). Thin line: no truncation. Other truncations represented are 90% (dot-dash line), 80% (dotted line) and 70% (dashed line)

We experimented with truncating the spectra at different levels below the continuum, both to gauge the effect of avoiding contamination from weak lines in a faint secondary spectrum, and also to discover whether the line cores produced a more reliable signal than did the total line profiles. Figures 4a and 4b show the results for Windows 3 and 1. Cut-offs at 90% or 95% produced almost the same results as no cut-off at all (though with one notable exception), whilst truncating the spectra below 90% induced large systematic trends. The exception was HR104, long documented as a single-lined spectroscopic binary (Udick 1912) but in which very weak lines from its faint companion have more recently been discerned on low-noise spectra (Hill et al. 1993). The influence of its faint secondary is very evident from the large excursion in the thin line (no truncation) at (B-V) = 0.03, and clearly has to be avoided; the possible influence of a faint spectroscopic companion is investigated from a more general point of view in Sect. 5.5. We found that excluding the continuum tended to improve the contrast and the cleanness of a CCF. We therefore decided to truncate all the spectra at 95%, as a general compromise between including as much of the height of each feature as was reasonable whilst at the same time excluding any contribution from a secondary spectrum that might be present but scarcely visible. We note, however, that in so doing we may have biased the CCF by up to +0.2 kms^-1.

It is interesting that Window 1 shows relatively little variation of RV shift with cut-off level for the cooler half of the diagram, ranging from about 0.4 kms^-1 at (B-V) = 0.1 to 0.2 kms^-1 at (B-V) = 0.5. We attribute that apparent lack of sensitivity to the fact that Window 1 includes the Balmer lines, whose effects on the CCF are dominant and do not alter much if the cut-off level is dropped from the continuum down to 70%.

4.2 Assessment of internal errors

Our scheme for imposing a zero-velocity wavelength frame conveniently avoids external systematic errors arising from comparisons with arc spectra, but internal errors are of course inevitable. We first consider the main error sources individually and then attempt to judge their total size by comparing sub-sets of spectra of the same objects.

4.2.1 Sources of internal errors

Among the internal errors, both random and systematic contributions can be identified. Photon noise causes a truly random error on the spectra, in the sense that the errors on neighbouring pixels are not correlated (except, probably mildly, through the process of rebinning). There may also be other errors which arise randomly in the process of observation, but which vary on a scale much larger than the sampling step and could therefore be regarded as systematic, depending on the use that is made of them. For example, a non-uniform distribution of detector grains can adversely affect a line's shape and symmetry (and hence its position), the problem increasing as spectral lines are weakened for reasons associated with a star's spectral type, or (more importantly) broadened through rotation; local infelicities in the clear-plate level might have a similar effect. The level of those errors is partly reflected in the S/N values in Table 1. We mention parenthetically that line intensities measured photographically are subject to errors in the calibration procedure, but those have no impact upon line positions; in any case, comparisons of spectra in instances of multiple exposures used in this study showed satisfactory interagreement. The random errors in the spectra propagate into the CCF (albeit at a much reduced level, which is of course the main advantage of cross-correlation) and thus cause a random error in the measured RV shift. This last increases directly with the widths of the lines and inversely with the number of lines in a window. Its magnitude is therefore related to the nature of a spectrum (hence the "phenomenological'' approach announced above), and is difficult to quantify in general terms.

Unlike most centroiding algorithms, the procedure described in Sect. 4.1 does not involve any model-fitting, so we thus eliminate at least the possibility of a systematic error arising from the fact that the model to be fitted does not describe exactly the underlying function whose position one is trying to determine. Instead, however, it adds a contribution to the random error owing to the fact that the position of even a noise-free peak cannot be read back with infinite precision. Nevertheless, for a strong, symmetrical CCF the method of measuring the peak position by inverting it precludes an uncertainty of < 0.03 bins, or 0.02 kms^-1 since the spectra are binned in steps of 0.75 kms^-1 (10 mÅ). That uncertainty is very modest compared to the total internal errors described in Sect. 4.2.2.

Possible errors in stellar wavelength scales have been addressed in Sect. 3.6, where the systematic error in a wavelength scale was estimated to be 0.02 - 0.1 kms^-1, the upper limit being judged from the way in which we were obliged to handle each spectrum reduction separately in the face of a lack of full agreement between the two halves of an exposure. We feel confident, however, that by treating each half of an exposure separately those errors were kept to a minimum - as will in fact be borne out by the small sizes of the total internal errors, at least part of which are random. Other systematic errors may arise from the process of levelling, which may be somewhat subjective when bridging the broad profile of a Balmer line or when smoothing a local irregularity in the background intensity, but are only of second-order importance here.

These systematic errors in the spectra deform the CCF, contributing an error to the measured RV shift. However, despite its undoubtedly systematic origin, this error is not necessarily to be regarded as itself systematic, i.e. it is not necessarily correlated with errors of the same origin in comparable measured RV shifts. In fact, an error in the wavelength scale does not amount to a uniform offset but is a (slowly) varying function of the wavelength, depending on several factors which are themselves random in nature (e.g. noise in the lines which were selected to define the wavelength solution) or whose distribution among the sample of stellar spectra is heterogeneous - such as the nature of an individual spectrum (chemical composition, line widths and profiles) or a tendency for a temperature-based dependence upon different solar wavelengths. Thus, an error in the wavelength scale is generally not reproducible (or only partly reproducible) from one spectrum to the next, even among spectra of identical objects. Likewise, an error in the function used for levelling, though systematic within a given spectrum where it has to perform a specific task, will not be identical for different spectra. So when we compare two measurements of position, the error in either can have a contribution originating from "systematic'' effects but generally those contributions are not (or only weakly) correlated and may therefore be treated as contributions to the random error of the measurements.

The above conclusion is of course based upon the specific nature of the data we are using here and cannot be generalized to all systematic errors in any other kind of spectra. Even in the present case it has to be used with caution, because one can conceive of situations where it is not valid; for example, if spectra are cross-correlated against the same template within a window which is sufficiently narrow that an error in the wavelength scale is approximately constant over that window, an actual bias will be caused in the series of measurements. But fortunately our main conclusions do not rely upon any such special cases.

The fact that, for our present purposes, all internal-error sources can be considered as (at least largely) random allows us to describe their combined effect on the measurements by a single number, the total internal error (see Sect. 4.2.2). The penalty we would incur in so doing, were the assumption of randomness not justified, is an over-estimate of the error in the sense that a series of independent identical estimates would yield values distributed around a non-zero mean, with a standard deviation less than the size we shall adopt for the total internal error.

4.2.2 Estimating the total internal error

We divided the 8 spectra of 32 Aqr into two independent sub-sets, and performed the cross-correlations described at the beginning of Sect. 4.1. We also selected 4 independent pairs of 32 Aqr spectra and carried out the same tests. We repeated that procedure for the 11 spectra of HR 7664 and the 13 of o Peg, but in the latter case just one pair of individual spectra, selected at random, was included in the error analysis. As discussed above, the magnitude of the error is largely expected to vary inversely with the width of the window, so we examined separately the errors shown by these internal cross-correlations in two groups of windows: (a) wide to medium-wide (Windows 1 to 4, 7, 10 and 12), and (b) small, i.e. 35 Å wide or less (Windows 5, 6, 8, 9, 11, 13, 14, 15).

The results for the two A-type stars (o Peg and 32 Aqr) showed that the internal errors in individual spectra are near 0.06 kms^-1 and unlikely to exceed 0.1 kms^-1 for large windows, while for small windows they are near 0.1 kms^-1 and unlikely to exceed 0.15 kms^-1. For averages of 4 or more spectra the above estimates are halved, e.g. around 0.03 kms^-1 and not exceeding 0.05 kms^-1 for large windows. HR 7664 (Bp) was included as an extreme case in which the density of lines is substantially lower than in the other spectra. The internal errors proved to be about twice as large for the larger windows but could rise to 3 or 4 times that amount for the smallest windows, indicating the sort of deterioration in the precision that must be expected for spectra with relatively few strong or medium-strong lines. For this star we also investigated whether the choice of cut-off level affected the internal errors, and found a small but systematic reduction in the standard deviations when a cut-off of 95% was imposed, as compared to no cut-off, thus adding a small extra weight to the decision to truncate spectra below the continuum level in order to avoid any weak secondary-star lines (Sect. 4.1.2). In general, the results of these particular tests demonstrate that the internal errors in our spectra are relatively minor and do not materially affect our main results.

4.3 Other errors

Mismatch shifts are small, so a careful assessment of all errors that might contribute is particularly important. Although the tests discussed in the previous section yield a realistic estimate of the internal errors, there are two other possible sources of systematic error - bias and sampling - to be discussed. Their effects are likely to be much smaller in cross-correlations without spectrum mismatch than in those which are the object of our study; they therefore cannot have contributed significantly to the internal error levels obtained above.

Bias may be caused by truncating the spectra slightly below their continuum levels, as mentioned in Sect. 4.1.2. For the reasons explained there we have chosen not to avoid it, but we did monitor its effects and we confirmed that it did not affect our conclusions regarding mismatch shifts. In any practical RV measurement where truncation is judged to be adviseable, this systematic error must be regarded as an independent bias; its contribution can be estimated for the spectra to hand by the sort of simple comparison illustrated in Fig. 4.

Another kind of systematic error might be anticipated to originate from interpolating the CCF position between sample steps when the CCF is asymmetrical. It would be detected as a correlation between the error in a measurement and the measurement itself. However, tests with high S/N spectra shifted over known fractions of a sample step revealed no such correlation. That result confirms that the error originating from the measurement process is in fact random, as already assumed in Sect. 4.2.

The absence of any systematic error in our process of measurement is probably due both to the high resolution of our spectra (relaxing the demands on interpolation) and to the nature of our centroiding algorithm. The latter leaves the user in complete control of the measurement (see Sect. 4.1), so any particular asymmetry can be dealt with judiciously as the situation requires. In cases of moderate asymmetry, the procedure of fitting the central region of the CCF implied that the interfering elements were considered to be secondary and were effectively ignored (though in cases of much more severe CCF asymmetry that were encountered exceptionally in the extremes of some of our tests, the measurement was abandoned). It was on account of asymmetrical CCFs that we regarded cross-correlations involving the Vega spectrum as less reliable than most (see Sect. 5.7).