4 The time dependent point spread function of the interferometer

   
4.1 Building the optical transfer function

This section describes the computation of the point spread function (PSF). As the PSF is the image of a point source the function $o(\vec{x})$in Eq.(1) becomes a $\delta$-function corresponding to a constant spectrum $O(\vec{u})$.

The spacing of the fringes that one obtains with an interferometer depends only on the shape of the exit pupil, or better, its autocorrelation, the OTF. In Fig.5 we show three different one dimensional pupil functions and their corresponding MTFs. The first two pupil functions show multiaxial beam combination, the last coaxial beam combination. If the pupils are so close together that the peaks in the OTF are overlapping, the information in the interferometric peaks cannot be fully retrieved. A loss of information in the interferometric peaks means a limit in the interferometric field-of-view. This can be understood if one remembers that an extended object leads to variations on small scales in the object complex visibility, which are not retrievable anymore in the entangled peaks. Using coaxial beam combination, one cannot disentangle the interferometric signal from the photometric signal anymore, since all peaks fall on top of each other (see Sect.4.3).

Figure 5: One dimensional pupil functions (left) and modulation transfer functions (right) for exit pupil separations of 2, 1, and 0 (pupil separation being the distance between the two pupil centers in pupil diameters). The solid lines in the MTFs show the three single parts of the MTF, the dashed lines (where visible) show the total MTF

In our approach we construct the pupil function and then calculate the OTFfrom the output of the interferometer simulations described in Sect.3. Since we must have access to all parts of the OTF separately without mixing them, we are internally computing the OTF always with well separated pupils and rearrange the peaks later to match the real OTF. A simulated two dimensional MTF for image plane beam combination with two telescopes and well separated exit pupils can be seen in Fig.6.

Figure 6: Modulation transfer function (MTF) for a multiaxial beam combiner. The structure of the MTF is mainly given by the autocorrelation of two uniform disks

The outputs from the optomechanical model are static electric field maps, dynamic Zernike coefficients for the time-dependent OPL maps, and the dynamic lateral pupil positions. For each of the two input polarizations there are three static electric field maps, corresponding to the three Cartesian components of the electric field. To reconstruct the exit pupil function from this output for a certain point in time, we take the static electric field maps and multiply them with the dynamic phasors exp $(j \Delta \phi_i(\vec{x},t))$ (see Eq.5). To simulate the combination of beams of different sizes (e.g. VLTI beams related to UT and AT) we use a virtual beam expander/compressor adjusting the beams to the same diameter.

From the vectorial pupil function $\vec{P}^{Pol}$ (Eq.4) one gets the internally used OTF^Polby computing its autocorrelation (Goodman 1968):

$$OTF^{Pol}(\vec{u}) = \frac{\vec{P}^{Pol}(\lambda{}\vec{u}) \... ...lambda{}\vec{u}) \right\vert^2 {\rm d}\vec{u}}; Pol \equiv s,p$$ (8)

where $\vec{u}$ is a two-dimensional, dimensionless vector in the spatial frequency domain ( $\vec{u}=\vec{x}/\lambda$). Within the model, the calculation of the OTF is performed using two Fourier transforms:

$$OTF^{Pol} = AC[\vec{P}^{Pol}] = F\{\left\vert F^{-1}\{\vec{P}^{Pol}\}\right\vert^2\}.$$ (9)

The simulation of the imaging process as described in Sect.2 is done independently for the two star polarizations ($s,\,p$) using the two transfer functions $OTF^s(\vec{u})$ and $OTF^p(\vec{u})$.

This way we construct an OTF_i for every timestep t_i of the dynamic simulation. The length of a single simulation interval $\Delta{}t\,=\,t_i-t_{i-1}$is chosen to ensure stationarity of the atmospheric perturbations. Over an exposure time T we have typically a few OTFs. It is the change of the OTF with time, which is degrading the interferometric signal, and in which we are interested. One gets the OTF for the whole exposure time when averaging the OTF_i.

Since the dimension of the electric field is $[{\rm V/m}]$, the autocorrelation above has the dimension ${\rm V}^2/{\rm m}^2]$. One retrieves intensities in $[{\rm W/m}^2]$ when multiplying by $0.5 \sqrt{\mu_0/\epsilon_0}$ with $\mu_0$ and $\epsilon_0$ being the dielectric constant and the permeability in vacuum. From here one comes to energies (and finally photons) by multiplying with the area of the beam Aand the length in time of the single simulation interval $\Delta{}t$.

The OTF constructed in this way is not dimensionless as described in Eq.(8), but already holds the photometric information. The object complex visibility we are multiplying with this OTF thus has to be dimensionless and normalized to one. Since we are using one object complex visibility for each polarization, the sum of these two visibilities has to be normalized. For an unpolarized object these two visibilities are identical and normalized to 0.5.

Since the OTFs already hold the intensity information, one can directly read the correlated flux for a point source from the OTF. It is the sum of the maxima of the interferometric peaks (or twice the height of one peak). The total flux is the maximum of the photometric peak, the uncorrelated flux is then the difference between the total flux and the correlated flux. It should be kept in mind that the two interferometric peaks are symmetric and carry exactly the same information. An extension of the described method to the case of extended objects is given in Sect.5.

The combination of more than two beams is performed by using the same method as for two beams. To compute the OTF, the N beams have to be arranged in a non-redundant way allowing to retrieve the photometric peak and the N(N-1)/2 interferometric peaks. Afterwards one has to rearrange them according to the exit pupil.

   
4.2 Multiaxial ("image plane'') beam combination

For combining the beams in the image plane the exit pupils of two or more interferometer arms are aligned side by side in the pupil plane (see Fig.7). Imaging this plane by an optical subsystem results in a spatial fringe pattern. The exit pupils have to be aligned so there is no redundancy in the distances between them. Usually the exit pupils are set on a line, with non redundant spacing, leaving the perpendicular axis available for spectroscopy (see Fig.8). A more compact setup can be achieved by using two dimensions, taking for example a trapezium structure with four exit pupils (Fig.9).

Figure 7: Multiaxial beam combination with fringe detection in an image plane

Figure 8: Non-redundant pupil function and the corresponding modulation transfer function for four beams and a linear setup

Figure 9: Non-redundant pupil function and the corresponding modulation transfer function for four beams and a compact setup

When observing in multiaxial mode one frame per atmospheric coherence time is taken. A usual method for estimation of the visibility amplitude V for an interferometer combining two beams, which have been spatially filtered to the extent of a single aperture Airy disk, is given in Roddier & Léna (1984): By taking the Fourier transform and squaring it one computes the power spectrum (squared MTF) of the spatial fringe pattern. The power spectrum has non-overlapping low and high-spatial frequency terms (the single photometric peak and the two interferometric peaks). The ratio of the high to low frequency energies gives a good estimation of the term $\frac{1}{2}\,V^2$.

For observations with a field-of-view exceeding the size of an Airy disk, one has to evaluate the values at every single spatial frequency within the interferometric peaks of the power spectrum.

This mode will be used by the AMBER beam combiner for the VLTI (Petrov et al. 1998). In Fig.10 a simulated image plane combined interferogram can be seen.

Figure 10: Image plane combined interferogram as observed in the focal plane of a Fizeau interferometer with three circular 1.8m subapertures (wavelength 550nm, effective focal length 34.65m, logarithmic dB-scale (relative to maximum)). The baselines have a length of 1.8m, 3.6m, and 5.4m

   
4.3 Coaxial ("pupil plane'') beam combination

Most interferometers are combining the beams coming from the arms of the interferometer in the pupil plane. This means that the exit pupils are aligned pairwise on top of each other. Afterwards usually an optical subsystem focuses the pupil on a detector (see Fig.11).

Figure 11: Coaxial beam combination with fringe detection in an image plane

To measure the fringe, the observer has to step through the fringe in time, namely modulating the optical path in one of the interferometer arms. One way to achieve this is to take four frames per atmospheric coherence time, each of which has (0, 1, 2, 3) $\times\lambda/4$ optical path difference (OPD) added to one beam. The visibility is estimated by determining the energy in each of the four frames ( A, B, C, D) and computing the modulus of the object complex visibility according to: $\frac{1}{2}\sqrt{(A-C)^2+(D-B)^2}$. The phase of the object complex visibility can also be computed from the four energy bins A, B, C, D (Shao & Staelin 1977).

For the beam combination in the model this means that one has to add 0, $\pi /2$, $\pi$, $3\pi /2$to the phase in one of the interferometric OTF peaks, and subtract the same value in the other interferometric peak. Figures12 and 13 illustrate what consequence this additional phase has on the OTF.

Figure 12: Optical transfer function for two rectangular apertures (multiaxial beam combination, exit baseline has the length of twice the pupil diameter), where a phase of $0, \pi /2, \pi ,$ and $3\pi /2$ is added to one of the beams. The interferometric peaks of the OTF are rotating around the complex axis. (Shown just for illustration since there is no path modulation necessary in multiaxial beam combination)

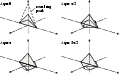Figure 13: Same as Fig.12, but for a coaxial beam combination. In the upper left the two interferometric peaks are enhancing the height of the photometric peak (no phase shift), in the two right drawings the interferometric peaks cancel, leaving only the photometric peak (phase shifts $\pi /2$ and $3\pi /2$), while in the lower left the two interferometric peaks cancel the photometric peak, leaving no signal (phase shift $\pi$)

This beam combination mode is foreseen with the MIDI instrument for VLTI (Leinert & Graser 1998). Four Airy disks of varying intensities, which form a typical interferogram can be seen in Fig.14.

Figure 14: Pupil plane combined interferograms at 10$\mu$m for delays of 0, $\lambda /4$, $\lambda /2$, and $3\lambda /4$(square root display). The lower left interferogram should be 0 over the whole image for a perfect interferometer and an unresolved object. This is not the case because of non-zero optical path difference (OPD) between the two arms of the interferometer and optical aberrations. Since the interferometric information is the total intensity on the detector, in real applications only one pixel is needed to record the data

When combining more than two beams in coaxial beam combination it is necessary to sample the fringe with more than four steps in time. This leads to different steps in phase for the interferometric peaks, which are now rotating around the imaginary axis with different speed. One of the beams is not delayed at all as another beam has to be delayed by steps of $\lambda /4$, just like in the case of two beam combination. The third beam has to be delayed with steps of $\lambda{}/12$. A total of 12 exposures has to be taken. For the six interferometric peaks of the OTF follows that two have to rotate by steps of $\pi /2$, two with $\pi/3$, and the last two with $\pi/6$. The first make three rotations during one fringe acquisition, the second two rotations, and the latter one rotation.

   
4.4 Taking temporal coherence into account

Within the modeling software we assume the validity of the quasi monochromatic approximation. A finite bandwidth of the source which is much smaller than the center wavelength/frequency can however be taken into consideration. This leads to a degradation of the visibility. In the picture of correlated versus uncorrelated flux this means that the correlated flux becomes less. Thus one has to lower the interferometric peaks in the OTF by a generally complex factor $\gamma$ $(0 \leq \left\vert \gamma \right\vert \leq 1)$. $\gamma$ is the degree of temporal coherence. It is a function of the OPD between the two interfering wavefronts and is computed as the Fourier transform of the power spectral density of the source (Goodman 1985). As a first approach we average the OPD between the beams across their areas and multiply the interferometric peaks in the OTF with this value. If the average OPD substantially exceeds the coherence length of the starlight the degradation factor $\left\vert\gamma\right\vert$ becomes zero and the fringes disappear. This computing approach does not consider a variation of the OPD across the beam areas.

   
4.5 Simulating polarized objects

A polarized object can be characterized in every pixel of the intensity distribution by three quantities: the flux, the degree of polarization, and the direction of polarization. In the model the polarized and the unpolarized flux are separated. The polarized flux is projected on the two polarization axes used within the optomechanical model. The unpolarized flux of the object is divided by two and added to the two polarization maps. From these two maps we calculate two object complex visibilities. Both are multiplied with their corresponding OTFs. Now the two different visibilities have to be added to retrieve the measured signal.