3 Computing the dynamic instrument response

For the simulation of the aperture synthesis imaging process of an interferometer the knowledge of the time-dependent optical transfer function (OTF) is of central importance. The OTF is given by the autocorrelation of the pupil function, i.e. the two-dimensional distribution of the complex electric field in the interferometer pupil plane when observing an point source. The task of computing the time-dependent electric field output of the different interferometer arms for a given baseline is performed by an optomechanical End-to-End model (EM). An EM contains models for structural mechanics, control system, sensors, actuators, various perturbations (e.g. atmospheric turbulence, wind), and - as a core part - an optical model which computes the optical signal flow through the instrument. For realistic simulation of the control loop sensors the source intensity in the respective wavelength range has to be taken into account. Modeling the fringe sensor performance requires the knowledge of the object visibility for the given baseline.

3.1 Modeling interferometer optics

We have developed a novel optical modeling tool (OM) which is specifically designed to meet the requirements for simulation of ground- and space-based astronomical interferometers (Wilhelm et al. 1998; Wilhelm & Johann 1999). A fast coordinate-free ray tracing algorithm (Redding & Breckenridge 1991) forms the basis of the OM. Diffraction propagation is handled either by numerical approximation of the Rayleigh-Sommerfeld integral or by Fourier-optical methods based on the Fast Fourier Transform (FFT). A Jones matrix formalism keeps track of the vectorial electric field. The OM includes a photometry algorithm which calculates the calibrated power flux through the instrument. In contrast to stochastic ray tracing methods of some commercial optical design programs our method makes use of a triangle grid interconnecting the rays. Each triangle is interpreted as an energy-carrying surface element of a locally planar wavefront. Beam propagation is modeled by a sequence of geometrical and physical-optical propagations. The choice of the adequate propagation model (geometrical/physical optics) for a single propagation step between two optical surfaces is made with respect to the respective "beam geometry'', i.e. the relative sizes of beam diameter, wavefront curvature, optical element aperture and wavelength.

Figures2 and 3 show scaled models of a VLT Unit Telescope and a VLTI optical delay line, both established with the OM.

Figure 2: Scaled model of a VLT unit telescope established with the optical modeling tool. The optical system is subdivided into three groups: (1) telescope optics (M1, M2, M3), (2) Coude train (M4... M8), (3) relay optics (M9... M11). The collimated beam at the telescope output (after reflection at M11) has a diameter of 8 cm. The coordinates (u,v,w) denote the VLTI site coordinates commonly used in ESO publications

Figure 3: Scaled model of a VLTI cat's-eye optical delay line established with the optical modeling tool. The optical design is of the "Ritchey-Chretien'' type: a telescope with a tertiary mirror at the focus which sends the beam back in a direction parallel to the one it came from. Apart from equalization of the optical path differences the delay line serves the purpose of imaging the exit pupil of a telescope to a fixed location inside the beam combination laboratory. Technically this is accomplished by actively controlling the curvature of the tertiary mirror (M15)

3.2 Computing the static electric field maps in the pupil plane

The observation of a point source is simulated by propagating a plane wave through each interferometer arm using a sequence of geometrical and physical-optical propagations. To simulate a naturally polarized starlight beam the computation is done sequentially for two uncorrelated, linearly polarized beams with mutually perpendicular polarization directions ("s'' and "p'') defined in the plane of the incident wavefront. The vectorial electric field distribution in the pupil plane is computed for each "star polarization'' (s, p):

$$\vec{P}^{Pol}(\vec{x}) = {\vec{E}}_1^{Pol}({\vec{x}}) + {\vec{E}}_2^{Pol}({\vec{x}}); Pol \equiv s,p$$ (4)

where $\vec{x}$ denotes a position in the pupil plane and the subscripts "1'' and "2'' correspond to the two interferometer arms. The function $\vec{P}^{Pol}$ is the vectorial pupil function which is used to compute the static OTF (see Sect.4).

Figure4 shows the distribution of the electric field amplitude and phase (one Cartesian component) in the exit pupil plane of a single VLTI arm (one interferometric beam). The field maps result from a hybrid propagation model combining geometrical- and physical-optical propagations. As the propagation of the starlight beam is within the near-field regime the beam diameter at the exit pupil does not substantially deviate from the 8 cm geometrical-optical footprint (indicated by the white circle in the amplitude map). 92.8% of the optical power is received within the 8 cm circular footprint for a wavelength of 2$\mu$m. On the other hand the amplitude pattern shows significant diffraction effects (typical "near-field ripples''). The phase variation across the 8 cm diameter corresponds to approximately one wavelength (phase difference $\approx 2\pi$). Outside the 8 cm circle the slope of the phase map is significantly bigger leading to a rapid oscillation between 0 and $2\pi$.

Figure 4: Field amplitude [V/m] (top) and phase [in units of $\pi$] (bottom) of one Cartesian component of the complex electric vector field in the exit pupil of a VLTI arm related to a Unit Telescope observing a point source ( $m_{\rm K}\,=\,10$). The two-dimensional field amplitude distribution is plotted in a 10 cm $\times$ 10 cm square defined in the exit pupil. The phase plot shows a cut through the two-dimensional phase map in theu-direction. In both plots the 8 cm geometrical-optical footprint of the starlight beam is indicated

3.3 Computing the time-dependent electric field maps in the pupil plane

Up to this point we have described the computation of the static electric field distributions. The calculation of the dynamic OTFs requires the knowledge of the time-dependent electric field distributions $\vec{E}_1^{Pol}(\vec{x},t)$and $\vec{E}_2^{Pol}(\vec{x},t)$. Therefore the OM is integrated into an EM. We have implemented the OM described above within the VLTI End-to-End Model, developed at ESO (Denise & Koehler 1998; Wilhelm & Koehler 1998). It simulates the dynamic response of the VLTI to a point source. Engineering objectives include the analysis of collective effects of disturbances and the study of interaction of optics and control loops. Eventually, the model is planned to be used as a diagnosis tool during the commissioning of the instrument. Simulated disturbances are wind load on telescopes, atmospheric wavefront piston and tip/tilt, and seismic noise. Atmospheric scintillation and high-spatial frequency corrugations of the wavefront are not taken into account. Mechanical structure modeling is done off-line using finite element software. The response of the interferometer to disturbances is then modeled in the End-to-End model using transfer functions between the disturbances (e.g. wind load) and optical parameters (e.g. optical path length (OPL)). The dynamic control environment model uses a "linear optical model'' ("small-motion model''). A linear optical model is represented by a sensitivity matrix characterizing the dynamic behavior of a set of optical output parameters in the presence of perturbations acting on the optical system. Examples for optical output parameters are the changes in the position or optical path of a ray or the changes in the Zernike coefficients representing the optical path distribution of a wavefront. The usage of a linear optical model assumes that the perturbations (translations and rotations) of the optical surfaces are small enough to ensure proportionality between the changes in output parameters and the perturbations.

For computation of the dynamic pupil function it is assumed that the time-dependent electric vector field $\vec{E}_i^{Pol}(\vec{x},t)$ in the exit pupil of an interferometer arm i is given by the product of a static vector field $\vec{E}_i^{Pol}(\vec{x})$ and a time-dependent phase factor

 

$$\vec{E}_i^{Pol}(\vec{x},t) \vec{E}_i^{Pol}(\vec{x})\,{\rm e}^{j\,\Delta\phi_i(\vec{x},t)}$$ = (5)

$$(i\equiv{}1,2; Pol\equiv{}s,p).$$

The time-dependent "phase error'' $\Delta\phi_i(\vec{x},t)$ arises from fluctuations of the optical path in the exit pupil with respect to the static situation. As the displacements of the optical elements due to the disturbances and active control are sufficiently small the resulting phase error can be regarded as polarization-independent, i.e. the same factor exp $(j\,\Delta\phi_i(\vec{x},t))$ is applied to all Cartesian components of the electric vector field. The equation $\Delta\phi_i(\vec{x},t) = (2\pi/\lambda)\,\Delta{}OP(\vec{x},t)$ links the phase error for a given interferometric arm ito an "optical path error'' $\Delta{}OP$ which itself can be expressed as a Zernike polynomial decomposition using M orthogonal Zernike polynomials $\Psi{}_m$ (typical number M = 15):

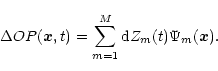$$\Delta{}OP(\vec{x},t) = \sum_{m=1}^M {\rm d}Z_m(t) \Psi{}_m(\vec{x}).$$ (6)

The M time-dependent coefficients dZ_m are the deviations of the MZernike coefficients with respect to the static situation. Within the dynamic simulation the coefficients dZ_m are computed by a linear optical model represented by a sensitivity matrix ${\bf A}$:

$${\rm d}{\bf Z}(t) = {\bf A} * {\rm d}{\bf p}(t)$$ (7)

where d ${\bf Z}(t)$ is a vector of size $M \times 1$ holding the deviations of the M Zernike coefficients, d ${\bf p}(t)$ is a vector of size $6N \times 1$ holding the perturbations (rotation and translation; 6 degrees of freedom per surface) of the N optical surfaces along a beam train and ${\bf A}$is a $M \times 6N$ sensitivity matrix. The computation of the sensitivity matrices for the different interferometer arms is done in the preprocessing phase of the EM by sequentially applying small perturbations to the optical surfaces, propagating the starlight beam and watching the changes in the Zernike coefficients in the respective exit pupils.

If the displacement of the exit pupils has to be taken into account appropriate sensitivity matrices can be defined analogously.