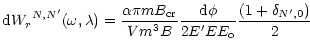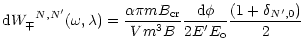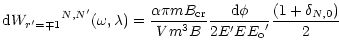Up: Polarization for pair annihilation
A single photon of energy
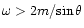 ,
with
,
with 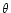 the photon emission
angle with respect to the magnetic field, may be produced by electron -
positron annihilation in a strong magnetic field.
This first order
process is permitted in the presence of an external magnetic field, which can
absorb the transverse momentum difference between the initial and final
particles.
the photon emission
angle with respect to the magnetic field, may be produced by electron -
positron annihilation in a strong magnetic field.
This first order
process is permitted in the presence of an external magnetic field, which can
absorb the transverse momentum difference between the initial and final
particles.
The S-matrix element for this process may be written in the form:
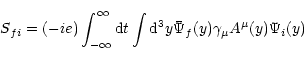 |
(1) |
with:
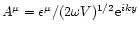 .
.
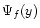 and
and 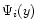 are the wave functions for positron and electron,
respectively. We used the wave functions for
are the wave functions for positron and electron,
respectively. We used the wave functions for  and
and  defined by
Sokolov & Ternov (1983).
defined by
Sokolov & Ternov (1983).
The photon has four possible polarizations to consider. The two linear
polarizations are defined by the unit vectors:
| |
|
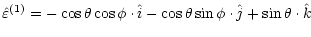 |
|
| |
|
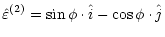 |
(2) |
where the photon momentum vector is given by:
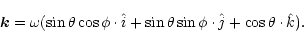 |
(3) |
The unit vectors
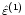 ,
,
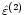 and
and
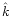 form a right handed triad:
form a right handed triad:
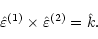 |
(4) |
The two circular polarizations (right-handed and left-handed
respectively) are given by:
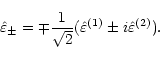 |
(5) |
The energies for 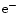 (E) and
(E) and 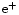 (
(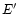 )
are:
)
are:
![$\displaystyle E {=} [ m^2{+}{p_z}^2 {+} 4N\gamma)]^{1/2};~
E^\prime{=} [ m^2{+}{p^\prime_z}^2 {+} 4N^\prime \gamma)]^{1/2}.$](/articles/aas/full/2000/11/ds9421/img78.gif) |
|
|
(6) |
Here pz is the longitudinal momentum for 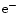 ,
,
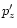 is the longitudinal momentum for
is the longitudinal momentum for 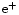 ,
N=0, 1, 2, ... is the Landau level of
,
N=0, 1, 2, ... is the Landau level of 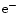 ,
,
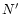 is the Landau level of
is the Landau level of 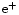 ,
and
,
and
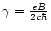 .
In natural units (
.
In natural units (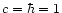 ),
which we adopt hereafter,
),
which we adopt hereafter,
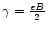 .
.
The probability for the annihilation process is:
| |
|
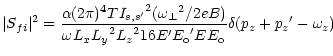 |
|
| |
|
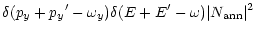 |
(7) |
with:
with
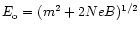 ,
,
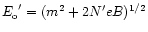 ,
and
,
and
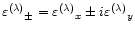 .
Formulae for
.
Formulae for
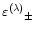 are given explicity in Table 1.
The polarization of the electron spin is
are given explicity in Table 1.
The polarization of the electron spin is
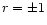 ,
except for N=0 which has r=-1 only.
The polarization of the positron spin is
,
except for N=0 which has r=-1 only.
The polarization of the positron spin is
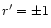 ,
except for
,
except for
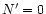 which has
which has
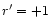 only.
only.
The Laguerre function is:
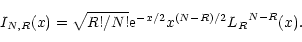 |
(9) |
If we sum over radial quantum number 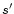 :
:
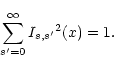 |
(10) |
However, the sum over s is limited to some maximum value
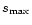 (see
Sokolov & Ternov 1983),
so
(see
Sokolov & Ternov 1983),
so
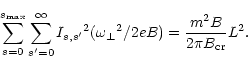 |
(11) |
The evaluation of the probability for the 1 photon annihilation
process using Sokolov's spinors is different with respect to the
evaluation using Herold's spinors (Herold 1979)
as follows.
We obtain one more term
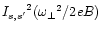 and only two laws of conservation:
and only two laws of conservation:
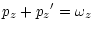 |
|
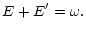 |
(12) |
In comparison
Wunner et al. (1986)
has one more conservation law
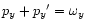 .
.
The transition rate is given by:
| |
|
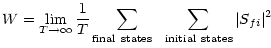 |
|
| |
|
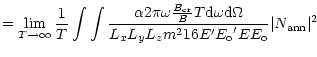 |
(13) |
with
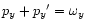 and
and
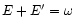 .
.
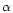 denotes the fine structure constant
(
denotes the fine structure constant
(
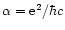 or
or 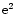 in natural units).
The differential transition rate is:
in natural units).
The differential transition rate is:
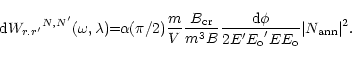 |
(14) |
Restricting to the case of zero longitudinal momentum for the electron
(pz=0), we obtain:
Here
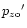 is the longitudinal momentum of the positron
when the electron longitudinal momentum is zero.
is the longitudinal momentum of the positron
when the electron longitudinal momentum is zero.
The energy of the annihilation radiation is given by:
This follows from the two conservation laws
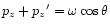 and
and
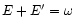 .
.
The coefficients above related to the polarization of the photon are
evaluated and listed in Table 2.
By averaging over polarization of the positron, the differential transition
rate for a polarized electron (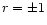 )
and unpolarized positron (if
)
and unpolarized positron (if 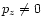 )
is:
)
is:
For the case of zero electron longitudinal momentum (pz = 0)
this reduces to:
Alternatively, if we average
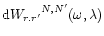 over the polarization of the electron, the differential probability for a
polarized positron (
over the polarization of the electron, the differential probability for a
polarized positron (
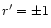 )
and an unpolarized electron is obtained (for
)
and an unpolarized electron is obtained (for 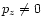 ):
):


Up: Polarization for pair annihilation
Copyright The European Southern Observatory (ESO)
![]() ,
with
,
with ![]() the photon emission
angle with respect to the magnetic field, may be produced by electron -
positron annihilation in a strong magnetic field.
This first order
process is permitted in the presence of an external magnetic field, which can
absorb the transverse momentum difference between the initial and final
particles.
the photon emission
angle with respect to the magnetic field, may be produced by electron -
positron annihilation in a strong magnetic field.
This first order
process is permitted in the presence of an external magnetic field, which can
absorb the transverse momentum difference between the initial and final
particles.
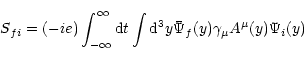
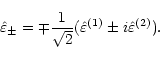
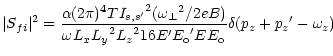
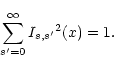
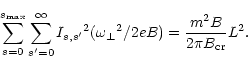
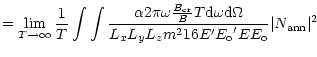
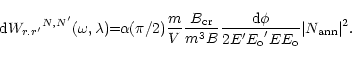
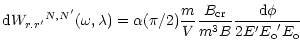
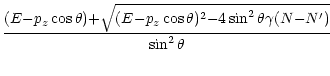
![$\displaystyle \frac {(E{-}p_z \cos \theta)} {\sin^2 \theta} \!\!\left[\!1\!{+}\...
...\prime) m^2 (B/B_{\rm cr}) \sin^2\theta }{(E{-}p_z
\cos \theta)^2}}\right]\cdot$](/articles/aas/full/2000/11/ds9421/img165.gif)
![]() )
and unpolarized positron (if
)
and unpolarized positron (if ![]() )
is:
)
is: