Integrating the differential rate ![]() over the azimuth angle,
over the azimuth angle, ![]() ,
and dividing the resulting rate by the current density
(
,
and dividing the resulting rate by the current density
(
![]() )
we obtain the one-photon
annihilation cross-section (for any pz):
)
we obtain the one-photon
annihilation cross-section (for any pz):
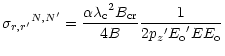 |
|||
| (20) |
If we suppose that ![]() and
and ![]() are found in the lowest Landau state
(
are found in the lowest Landau state
(
![]() )
and
)
and
![]() ,
so
,
so
![]() ,
then the photon is
emitted perpendicular to the magnetic field (
,
then the photon is
emitted perpendicular to the magnetic field (
![]() ). We
allow any polarization of the photon. Then
the above expression for the cross-section reduces to:
). We
allow any polarization of the photon. Then
the above expression for the cross-section reduces to:
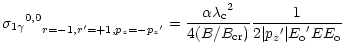 |
|||
| (21) |
| = | 0 | ||
| = | 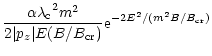 |
||
| = | |||
| = | (22) |
If we take the case of an electron with zero longitudinal momentum (pz = 0), and sum over polarization, then we find:
| = | ![$\displaystyle \frac {\alpha {\lambda _{\rm c}}^2 m}{\vert{p_{ z}}^\prime\vert (B/B_{\rm cr}) }
{\rm e}^{-[1+(1+({p_{ z}}^\prime/m)^2)^{1/2}] (B_{\rm cr}/B)}$](/articles/aas/full/2000/11/ds9421/img261.gif) |
(23) |
From the conservation laws:
![]() and
and
![]() ,
we find the expression for the longitudinal component
of the
,
we find the expression for the longitudinal component
of the ![]() momentum:
momentum:
| = | ![$\displaystyle \frac {(E \cos \theta -p_{z} ) + \sqrt{(E \cos \theta -p_{z})^2
-...
...(N^\prime- N)
-2 E p_{z} \cos \theta]}}
{{\rm sin}^2 \theta}\cdot \hspace*{4cm}$](/articles/aas/full/2000/11/ds9421/img263.gif) |
(24) |
| = | 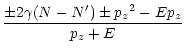 |
(25) |
If we average over the polarization of the ![]() and
and ![]() in Eq. (20)
above, we obtain:
in Eq. (20)
above, we obtain:
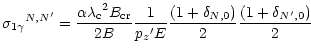 |
|||
| (26) |
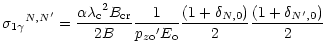 |
|||
| (27) |
Copyright The European Southern Observatory (ESO)