| (28) |
The decay rate per unit volume is calculated from the cross-section by
(e.g. Wunner et al. 1986):
| (28) |
| n(p) | = | (29) |
In order to carry out the integration over the longitudinal momentum
distributions, we use the relation giving pz for the electron from
the conservation laws, which is:
| (30) |
| pz | = | 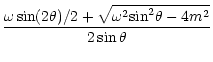 |
(31) |
For the specific cases presented here for the annihilation rate,
we take the electron and positron
distributions to be the same.
We take the case
![]() and
and
![]() keV,
keV,
![]() ,
and unpolarized radiation.
Figure 1 shows the annihilation rate as a function of photon emission angle
for
,
and unpolarized radiation.
Figure 1 shows the annihilation rate as a function of photon emission angle
for
![]() Gauss.
Figure 2 shows the same but for
Gauss.
Figure 2 shows the same but for
![]() .
Figure 1 is consistent with the result of Daugherty & Bussard (1980)
(however we give, in addition, the value of the decay rate):
the radiation is confined to a narrow beam centered at
.
Figure 1 is consistent with the result of Daugherty & Bussard (1980)
(however we give, in addition, the value of the decay rate):
the radiation is confined to a narrow beam centered at
![]() for low magnetic field and small
for low magnetic field and small ![]() .
Figure 2 shows that the annihilation rate increases rapidly with increasing
B (a factor of
.
Figure 2 shows that the annihilation rate increases rapidly with increasing
B (a factor of ![]() for an increase in B by a factor of 4.4)
but that the radiation remains well beamed.
We find that the beam is narrow for small
for an increase in B by a factor of 4.4)
but that the radiation remains well beamed.
We find that the beam is narrow for small
![]() and wide for large
and wide for large
![]() ,
for all values of B.
,
for all values of B.
Next we show some results of numerical evaluations of the cross-sections.
First we present cross-sections as a function of magnetic field for the
different photon polarizations.
The non-relativistic
free-space ![]() annihilation cross-section for
annihilation cross-section for
![]() pairs with
opposite spins and for the electron at rest (e.g. Wunner et al. 1986) is:
pairs with
opposite spins and for the electron at rest (e.g. Wunner et al. 1986) is:
![]() ,
with
,
with ![]() the velocity of the positron.
We present our cross-sections normalized by the non-relativistic
free-space
the velocity of the positron.
We present our cross-sections normalized by the non-relativistic
free-space ![]() annihilation cross-section.
The expression for
annihilation cross-section.
The expression for ![]() valid for also for a relativistic positron and
in the positron in any Landau state is:
valid for also for a relativistic positron and
in the positron in any Landau state is:
![]() .
We note that our calculations
of the normalized cross-sections for the cases given in Wunner et al. (1986)
agree with their calculations.
.
We note that our calculations
of the normalized cross-sections for the cases given in Wunner et al. (1986)
agree with their calculations.
For the case of
![]() and electron with spin down
and positron with spin up,
the following relations can be shown to hold:
and electron with spin down
and positron with spin up,
the following relations can be shown to hold:
![]() and
and
![]() .
For
.
For
![]() ,
the above is valid for any values of pz and
,
the above is valid for any values of pz and
![]() .
.
Figure 3 gives the annihilation cross-section, normalized to
![]() ,
for
,
for ![]() with N=0 and r=-1 (spin down), and
with N=0 and r=-1 (spin down), and ![]() with
with
![]() and
and
![]() (spin up). For all cases the electron
has pz=0. The positron has
(spin up). For all cases the electron
has pz=0. The positron has
![]() (in practise we use
a small value, like 10-20 MeV/c to numerically evaluate the cross-section)
in one case (with subscript 0),
and
(in practise we use
a small value, like 10-20 MeV/c to numerically evaluate the cross-section)
in one case (with subscript 0),
and
![]() for the second case (with subscript 2 mc).
Since
for the second case (with subscript 2 mc).
Since
![]() and
and
![]() ,
only the cross-sections
for photon polarizations
,
only the cross-sections
for photon polarizations
![]() (labelled
(labelled ![]() )
and
)
and
![]() (labelled
(labelled ![]() )
are plotted.
The cross-sections for unpolarized radiation (sum over polarization for
outgoing states) are not plotted, since they are equal to the
polarization
)
are plotted.
The cross-sections for unpolarized radiation (sum over polarization for
outgoing states) are not plotted, since they are equal to the
polarization
![]() cross-sections in this case.
cross-sections in this case.
We find that the cross-sections rise as a function of B rapidly to a
peak at
![]() and decrease slowly for larger B.
The peak values
are larger than the non-relativistic free-space annihilation cross-section
by factors of
and decrease slowly for larger B.
The peak values
are larger than the non-relativistic free-space annihilation cross-section
by factors of ![]() to
to ![]() .
For nonrelativistic parallel momentum,
.
For nonrelativistic parallel momentum,
![]() ,
one has:
for unpolarized radiation or for polarization
,
one has:
for unpolarized radiation or for polarization
![]() ,
,
![]() for
for
![]() ;
and for radiation polarization
;
and for radiation polarization
![]() or
or
![]() ,
,
![]() for
for
![]() .
For large parallel momentum (>mc), the annihilation rate is suppressed
compared to the small parallel momentum case.
For a relativistic parallel momentum of
.
For large parallel momentum (>mc), the annihilation rate is suppressed
compared to the small parallel momentum case.
For a relativistic parallel momentum of
![]() ,
one has:
for unpolarized radiation or for polarization
,
one has:
for unpolarized radiation or for polarization
![]() ,
,
![]() for
for
![]() ;
and for radiation polarization
;
and for radiation polarization
![]() or
or
![]() ,
,
![]() for
for
![]() .
For
.
For
![]() ,
one has:
for unpolarized radiation or for polarization
,
one has:
for unpolarized radiation or for polarization
![]() ,
,
![]() for
for
![]() ;
and for radiation polarization
;
and for radiation polarization
![]() or
or
![]() ,
,
![]() for
for
![]() .
.
Figure 4 gives the cross-section normalized to
![]() for the same cases
as for Fig. 3, except that the electron is now in an excited Landau level
(
for the same cases
as for Fig. 3, except that the electron is now in an excited Landau level
(![]() with N=1).
The positron has
with N=1).
The positron has
![]() in one case (with subscript 0),
and
in one case (with subscript 0),
and
![]() for the second case (with subscript 2 mc).
For
for the second case (with subscript 2 mc).
For
![]() ,
one has
,
one has
![]() and
and
![]() ,
so only the cross-sections
for photon polarizations
,
so only the cross-sections
for photon polarizations
![]() (labelled
(labelled ![]() )
and
)
and
![]() (labelled
(labelled ![]() )
are plotted.
The cross-section for unpolarized radiation (sum over polarization for
outgoing states) for
)
are plotted.
The cross-section for unpolarized radiation (sum over polarization for
outgoing states) for
![]() is equal to the
polarization
is equal to the
polarization
![]() cross-section.
However for nonzero positron momentum (here
cross-section.
However for nonzero positron momentum (here
![]() ),
the cross-sections for the different polarizations are all different.
The cross-section for unpolarized radiation (labelled
),
the cross-sections for the different polarizations are all different.
The cross-section for unpolarized radiation (labelled ![]() )
is
the largest of the 5 curves that peak below a value of 13, and in
decreasing order follow
)
is
the largest of the 5 curves that peak below a value of 13, and in
decreasing order follow ![]() ,
,
![]() ,
,
![]() (for photon polarization
(for photon polarization
![]() ), and
), and ![]() (for polarization
(for polarization
![]() ).
The
).
The
![]() case has lower (unpolarized radiation) cross-sections by a factor
of 2.5-3 compared to the N=0 case.
However it looks very different in
case has lower (unpolarized radiation) cross-sections by a factor
of 2.5-3 compared to the N=0 case.
However it looks very different in
![]() radiation,
which is not allowed in the N=0,
radiation,
which is not allowed in the N=0,
![]() case.
case.
![]() reaches a maximum as a function of B.
The maximum value and the B of maximum depend on N and
reaches a maximum as a function of B.
The maximum value and the B of maximum depend on N and ![]() .
E.g. for N=1 and
.
E.g. for N=1 and
![]() (Fig. 4),
the maximum value is 64.7, at
(Fig. 4),
the maximum value is 64.7, at
![]() .
.
The cross-section decreases with increasing longitudinal momentum. E.g.
for
![]() and N=1,
and N=1,
![]() (Fig. 4), the cross-section at
(Fig. 4), the cross-section at
![]() is
is
![]() times smaller than for
times smaller than for
![]() ,
and the cross-section at
,
and the cross-section at
![]() is 11.4 times smaller.
From Figs. 3 and 4, it can be seen that the
reduction in cross-section due to larger
is 11.4 times smaller.
From Figs. 3 and 4, it can be seen that the
reduction in cross-section due to larger
![]() is smaller for
larger B.
A second effect of larger
is smaller for
larger B.
A second effect of larger
![]() is that the cross-section reaches
maximum at larger B, and, for non-zero
is that the cross-section reaches
maximum at larger B, and, for non-zero
![]() ,
the B of
maximum depends on polarization.
E.g., for
,
the B of
maximum depends on polarization.
E.g., for
![]() N=1,
N=1,
![]() (Fig. 4): the maximum of
(Fig. 4): the maximum of
![]() has value
at the magnetic field of maximum as follows:
12.5 at
has value
at the magnetic field of maximum as follows:
12.5 at
![]() for sum over polarization;
11.6 at
for sum over polarization;
11.6 at
![]() for polarization
for polarization
![]() ;
1.17 at
;
1.17 at
![]() for polarization
for polarization
![]() ;
9.60 at
;
9.60 at
![]() for polarization
for polarization
![]() ;
and
3.18 at
;
and
3.18 at
![]() for polarization
for polarization
![]() .
For all values of B and r=-1,
.
For all values of B and r=-1,
![]() one has:
one has:
![]() .
.
We next compare the cross-sections for different spin states of the
electron.
In Fig. 5, the normalized cross-section is presented for
two different spin states: ![]() with N=1, pz=0 and
with N=1, pz=0 and ![]() ,
and
,
and ![]() with
with
![]() ,
,
![]() and
and
![]() .
The upper two curves (
.
The upper two curves (![]() for photon polarization
for photon polarization
![]() and
and ![]() for polarization
for polarization
![]() )
are for r=-1,
)
are for r=-1,
![]() (denoted by subscript du in the figure) and are the same as for Fig. 4.
The lower two curves (
(denoted by subscript du in the figure) and are the same as for Fig. 4.
The lower two curves (![]() for photon polarization
for photon polarization
![]() and
and ![]() for polarization
for polarization
![]() )
are for r=+1,
)
are for r=+1,
![]() (denoted by subscript uu).
Here and in what follows the first arrow indicates whether the electron
spin is up or down and the second arrow indicates whether the positron
spin is up or down (for the figures we use u and d to indicate spin up or
down).
For the case of
(denoted by subscript uu).
Here and in what follows the first arrow indicates whether the electron
spin is up or down and the second arrow indicates whether the positron
spin is up or down (for the figures we use u and d to indicate spin up or
down).
For the case of
![]() we have
we have
![]() and
and
![]() .
However for the case of electron and positron both spin-up
(
.
However for the case of electron and positron both spin-up
(
![]() ), we have
), we have
![]() and
and
![]() .
The cross-section for spins
.
The cross-section for spins
![]() is larger than that for
spins
is larger than that for
spins
![]() (e.g. by factor 22.0 at
(e.g. by factor 22.0 at
![]() ), the
difference decreasing with increasing B(e.g. by factor 1.56 at
), the
difference decreasing with increasing B(e.g. by factor 1.56 at
![]() ).
).
Generally for N>0 and
![]() (so both spins are allowed for positron
and electron) and if
(so both spins are allowed for positron
and electron) and if
![]() ,
one has the following relation for the cross-sections for different photon
polarizations:
For the cases with antiparallel spins (
,
one has the following relation for the cross-sections for different photon
polarizations:
For the cases with antiparallel spins (
![]() or
or
![]() )
we have
)
we have
![]() and
and
![]() .
For the cases with parallel spins (
.
For the cases with parallel spins (
![]() or
or
![]() )
we have
)
we have
![]() and
and
![]() .
In the above two cases we have the unpolarized cross-section is the same
as the
.
In the above two cases we have the unpolarized cross-section is the same
as the
![]() cross-sections.
For summing over polarization we have for all B:
cross-sections.
For summing over polarization we have for all B:
![]() .
Figure 6 shows the normalized cross-section for unpolarized radiation and for
four different spin states:
.
Figure 6 shows the normalized cross-section for unpolarized radiation and for
four different spin states: ![]() with N=2, pz=0 and
with N=2, pz=0 and ![]() ,
and
,
and ![]() with
with
![]() ,
,
![]() and
and
![]() .
The cross-section for r=-1,
.
The cross-section for r=-1,
![]() is denoted
is denoted
![]() ,
for r=1,
,
for r=1,
![]() is denoted
is denoted
![]() ,
for r=-1,
,
for r=-1,
![]() is denoted
is denoted
![]() ,
and for r=1,
,
and for r=1,
![]() is denoted
is denoted
![]() .
.
Next we consider the dependence of the cross-section on N and ![]() .
Figure 7 shows the normalized cross-section for
.
Figure 7 shows the normalized cross-section for
![]() spins
spins
![]() ,
summed over photon polarization,
for five sets of values of (N,
,
summed over photon polarization,
for five sets of values of (N,![]() ):
(3, 3), (5, 5), (10, 10), (15, 15) and (18, 18).
Here we have taken the case of longitudinal momentum:
):
(3, 3), (5, 5), (10, 10), (15, 15) and (18, 18).
Here we have taken the case of longitudinal momentum:
![]() .
(The case of zero longitudinal momentum and sum over polarization has been
considered by Wunner et al. 1986.)
Since
.
(The case of zero longitudinal momentum and sum over polarization has been
considered by Wunner et al. 1986.)
Since
![]() the relations in the last paragraph above give the
cross-sections for the individual polarizations.
I.e.,
the relations in the last paragraph above give the
cross-sections for the individual polarizations.
I.e.,
![]() and
and
![]() .
In Fig. 7, the number label on
.
In Fig. 7, the number label on ![]() represents the values of
N and
represents the values of
N and ![]() .
For small B (
.
For small B (
![]() ), the cross-sections at first
increase with N and
), the cross-sections at first
increase with N and ![]() then reach a maximum and
decrease for larger N and
then reach a maximum and
decrease for larger N and ![]() .
E.g. for
.
E.g. for
![]() ,
and
,
and
![]() Gauss), the maximum cross-section
is for
Gauss), the maximum cross-section
is for
![]() ,
and
,
and
![]() .
For large B (
.
For large B (
![]() ), one finds:
), one finds:
![]() is largest for for
is largest for for
![]() ;
and
;
and
![]() for
for
![]() decreases monotonically
with increasing N.
Generally we have the following relations for the relative size of the
cross-sections for different electron spins at fixed N and
decreases monotonically
with increasing N.
Generally we have the following relations for the relative size of the
cross-sections for different electron spins at fixed N and ![]() .
(a) For
.
(a) For
![]() ,
,
![]() (except for
(except for
![]() ,
where we only have the possibility for spins of
,
where we only have the possibility for spins of
![]() ).
(b) For
).
(b) For
![]() ,
,
![]() (except for
(except for
![]() ,
where we only have the possibilities for spins of
,
where we only have the possibilities for spins of
![]() and
and
![]() ).
(c) For
).
(c) For
![]() ,
,
![]() (except for N= 0,
where we only have the possibilities for spins of
(except for N= 0,
where we only have the possibilities for spins of
![]() and
and
![]() ).
).
Finally, we show a set of cross-sections for different N and ![]() (with
(with
![]() ), but rather than at fixed pz and
), but rather than at fixed pz and
![]() ,
they are
at fixed
,
they are
at fixed
![]() and
and
![]() .
In this case, because the
.
In this case, because the ![]() (or
(or ![]() )
energy increases with B for N>0 (or
)
energy increases with B for N>0 (or
![]() ), there is a maximum
B at constant
), there is a maximum
B at constant
![]() for N>0 (or at constant
for N>0 (or at constant
![]() for
for
![]() ).
Since we take
).
Since we take
![]() ,
the maximum B is the same for both
,
the maximum B is the same for both ![]() and
and ![]() .
Figure 8 shows the resulting normalized cross-sections as a function of
.
Figure 8 shows the resulting normalized cross-sections as a function of
![]() for six sets of values of (N,
for six sets of values of (N,![]() ): (0, 0), (1, 1),
(3, 3), (5, 5), (10, 10), and (15, 15) and for
): (0, 0), (1, 1),
(3, 3), (5, 5), (10, 10), and (15, 15) and for ![]() with spin down and
with spin down and ![]() with spin down and unpolarized radiation.
In all cases we have
with spin down and unpolarized radiation.
In all cases we have
![]() ,
so the relation for the different photon
polarization holds:
,
so the relation for the different photon
polarization holds:
![]() and
and
![]() .
.
In summary, we have presented formulae for the one photon pair annihilation cross-section for different photon polarizations which are valid for any magnetic field and any Landau and spin states of the electron and positron. These results are generalizations of those of Wunner et al. (1986). This is an important generalization, since the new results presented here allow calculation of the polarization of the emitted radiation, which is significantly different from zero, and strongly dependent on the momenta, spin and Landau states of the electron and positron.
Acknowledgements
DAL thanks the Natural Sciences and Engineering Research Council of Canada for support.
Copyright The European Southern Observatory (ESO)