| (13) |
We now consider the problem of discrimination between the chromospheric and coronal contributions to the polarized emission at different wavelengths bands and discuss the appropriate methods for magnetic field estimates. We rewrite Eqs. (11)-(12) as
| (13) |
| (14) |
Results of model calculations (Eqs. (13)-(14)) for a constant magnetic
field (with
![]() )
are presented in Fig. 1
versus
frequency for a plage region with parameters given in Eq. (10). As one can see
from Fig. 1, clear dominance of either chromosphere or corona, both in
intensity and polarization, exists only for high or low frequencies
respectively. When one of these contributions becomes dominant, we can use
Eqs. (13) and (14) (or Eq. 4) for magnetic field estimates in the corona
and chromosphere:
)
are presented in Fig. 1
versus
frequency for a plage region with parameters given in Eq. (10). As one can see
from Fig. 1, clear dominance of either chromosphere or corona, both in
intensity and polarization, exists only for high or low frequencies
respectively. When one of these contributions becomes dominant, we can use
Eqs. (13) and (14) (or Eq. 4) for magnetic field estimates in the corona
and chromosphere:
![\begin{displaymath}\lbrack B_{\rm cor}]=\frac{5350}{\lambda }\frac{V_{\rm cor}}{...
...]=%
\frac{5350}{\lambda }\frac{V_{\rm chr}}{qI_{\rm chr}}\cdot
\end{displaymath}](/articles/aas/full/2000/10/ds8262/img110.gif) |
(15) |
At long cm-wavelengths the coronal contribution becomes significant (Fig.
1), so that we could use Eq. (15a) to estimate the coronal magnetic
field.
However, the magnetic field in the photosphere and the corona
varies continuously. Therefore we establish, for a simplified model
atmosphere, the relation between the value of an inhomogeneous field (or its
parameter ![]() )
at some height h and its estimated value
)
at some height h and its estimated value ![]() , as derived from Eq. (4). We show that for magnetic fields varying
between the chromosphere and corona the estimate from Eq. (4) gives the
value of the magnetic field at the height of the transition region (TR), i.e.
near
the base of the corona, independent from wavelength and the magnetic field
profile.
, as derived from Eq. (4). We show that for magnetic fields varying
between the chromosphere and corona the estimate from Eq. (4) gives the
value of the magnetic field at the height of the transition region (TR), i.e.
near
the base of the corona, independent from wavelength and the magnetic field
profile.
We can approximate such an inhomogeneous atmosphere with a simplified model for
![]() and
and ![]() as
as
| (16) |
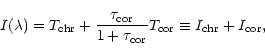 |
(17) |
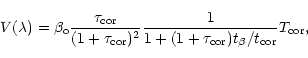 |
(18) |
![\begin{displaymath}\lbrack \beta (\lambda )]\equiv \frac{V(\lambda )}{\lambda
^{...
...1}{1+(1+\tau _{\rm cor})t_{\beta
}/t_{\rm cor}}\beta _{\rm o}.
\end{displaymath}](/articles/aas/full/2000/10/ds8262/img127.gif) |
(19) |
(a) in any optically thick isothermal medium (
![]() ), the
radiation temperature (
), the
radiation temperature (
![]() )
equals the kinetic temperature:
)
equals the kinetic temperature:
![]() (black body radiation), with the absence of polarization (
(black body radiation), with the absence of polarization (
![]() );
);
(b) in the optically thin emission from the corona (
![]() the
polarization spectrum
the
polarization spectrum
![]() is proportional to the coronal
brightness
is proportional to the coronal
brightness
![]() ,
and grows with
,
and grows with
![]() ,
which is an observational signature of the coronal origin of polarization;
,
which is an observational signature of the coronal origin of polarization;
(c) in the optically thick regime (
![]() )
polarization quickly
decreases, as for any black-body radiation;
)
polarization quickly
decreases, as for any black-body radiation;
(d) in the intermediate emission regime where
![]() the
polarization spectrum has a sharp maximum near wavelength
the
polarization spectrum has a sharp maximum near wavelength
![]() determined by
determined by
![]() 1.
1.
The bottom of the corona corresponds in our model to a normalised radiodepth of
![]() (Eq. 17), so that the model magnetic field strength
(Eq. 17), so that the model magnetic field strength
![]() at this level becomes:
at this level becomes:
| (20) |
| (21) |
| (22) |
![\begin{displaymath}\lbrack \beta (\lambda )]\equiv \frac{V(\lambda )}{\lambda
^{2}{\rm d}I/{\rm d}(\lambda ^{2})}\simeq \beta _{\rm TR}.
\end{displaymath}](/articles/aas/full/2000/10/ds8262/img146.gif) |
(23) |
As was shown above, the main contribution to the polarized emission originates
near the thin transition region. For this reason we can assume, that a
magnetic field is uniform in the region of formation of polarized emission
and use the equations above (Eq. (4) and Eqs. (13)) for the uniform case (
![]() ), as a first approximation.
Thus Eq. (4) can be used to estimate the magnetic field:
), as a first approximation.
Thus Eq. (4) can be used to estimate the magnetic field:
| = | |||
| n | 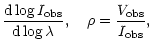 |
(24) |
From a single-frequency observation we have an another estimate
for the magnetic field from Eqs. (13):
![\begin{displaymath}\lbrack B]_{\rm G}=5350\frac{1}{\lambda _{\rm cm}}Q(\lambda
)\frac{V_{\rm obs}}{I_{\rm obs}},
\end{displaymath}](/articles/aas/full/2000/10/ds8262/img153.gif) |
(25) |
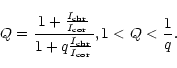 |
(26) |
From the single frequency observations of plage regions we are unable to determine either n or Q. They can be provided by our model simulation for observations (see Table 1 and Fig. 1). In addition, we can use simplified equations for the limiting cases at high and low emission frequencies:
(a) at long wavelengths with coronal domination in intensity
![]() for q<<1, we have
for q<<1, we have ![]() and
and ![]() (optically thin coronal
radiation), that Eq. (15) gives the magnetic field near the transition region:
(optically thin coronal
radiation), that Eq. (15) gives the magnetic field near the transition region:
![\begin{displaymath}\lbrack B]_{\rm G}=\frac{5350}{\lambda}\frac{V_{\rm obs}}{I_{\rm PL}},\ %
I_{\rm PL}\equiv \delta I_{\rm PL}+I_{\rm QS},
\end{displaymath}](/articles/aas/full/2000/10/ds8262/img161.gif) |
(27) |
| (28) |
In order to illustrate both limiting cases, we calculated typical values for
the expected Q-factor for Westerbork
![]() cm) and Nobeyama
cm) and Nobeyama
![]() cm) plage observations. We find for a typical plage area(s)
cm) plage observations. We find for a typical plage area(s)
![]() ,
and
,
and
![]() .
Therefore, with
Nobeyama observations at 17 GHz the chromospheric contribution is important
for more precise estimates.
.
Therefore, with
Nobeyama observations at 17 GHz the chromospheric contribution is important
for more precise estimates.
Copyright The European Southern Observatory (ESO)