Brightness contrasts above the magnetic network from recent VLA -
Yohkoh (SXT) observations of quiet Sun regions with arc sec
resolution (at ![]() = 1.3, 2.0, and 3.6 cm) were obtained by
Benz et al. ([1997]). Model simulations with current optical reference
atmospheres (Fontenla et al. [1993]) were inconclusive. In order to
solve the problems of model simulations we use here the results of
a multi frequency study (Bogod & Grebinskij [1997]) in a wide
range of mm - cm band microwave brightness observations with
moderate (arcmin) spatial resolution.
= 1.3, 2.0, and 3.6 cm) were obtained by
Benz et al. ([1997]). Model simulations with current optical reference
atmospheres (Fontenla et al. [1993]) were inconclusive. In order to
solve the problems of model simulations we use here the results of
a multi frequency study (Bogod & Grebinskij [1997]) in a wide
range of mm - cm band microwave brightness observations with
moderate (arcmin) spatial resolution.
The solar atmosphere at microwave frequencies can be considered (see Grebinskij [1987]; Zirin et al. [1991]) as a two-component medium with an optically thin corona and an optically thick chromosphere with small temperature gradients:
| (5) |
| = | |||
| < | 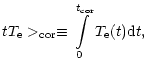 |
(6) |
For the chromosphere, we use a power-law electron temperature distribution, as
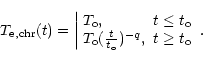 |
(7) |
| (8) |
The model has 4 free parameters (
![]() and
and
![]() ).
The same model is used both for the quiet Sun and plage
emission, but with different parameters. These are found by
modelling the observed brightness spectra.
).
The same model is used both for the quiet Sun and plage
emission, but with different parameters. These are found by
modelling the observed brightness spectra.
As observational spectra for model matching, we use here a combination of OVRO (Zirin et al. [1991]) and compiled (Bogod & Grebinskij [1997]) mm-band observations for different quiet Sun regions (as reference) in the frequency range of 87 - 1.4 GHz. For plage area(s) we use observations from Metsähovi at 87 - 22GHz (Urpo et al. [1987]), Nobeyama maps at 17 GHz, RATAN at 1.4 - 16 GHz (Bogod & Gelfreikh [1980]; Akhmedov et al. [1982]), and Westerbork at 5 GHz (Kundu et al. [1977]). With plage data we use the reported results of reduction of observed brightness excesses for moderate beam resolution.
The results of the brightness spectra simulations are well fitted by simple model with the following parameters:
| = | |||
| q | = | (9) | |
| = | |||
| q | = | (10) |
Taking into account the parameters above we can simplify the
Eq. (8). With q<<1 and
![]() at
at
![]() cm we can use the approximation
cm we can use the approximation
![]() and
and
![]() and obtain the total brightness spectrum
and obtain the total brightness spectrum
| (11) |
| Observed | Modelled | |||
|
|
|
|
|
|
| (GHz) | (103 K) | (103 K) | (103 K) | (103 K) |
| 1.4 | 70.5 | 3.0 | 70.6 | -0.1 |
| 1.6 | 63.8 | 2.8 | 58.6 | 5.2 |
| 1.8 | 52.2 | 2.5 | 50.0 | 2.2 |
| 2.0 | 42.9 | 1.9 | 43.5 | -0.6 |
| 2.4 | 32.8 | 1.4 | 34.7 | -1.9 |
| 2.8 | 27.1 | 1.1 | 29.1 | -2.0 |
| 3.2 | 24.2 | 1.1 | 25.3 | -0.9 |
| 3.6 | 21.7 | 1.1 | 22.5 | -0.8 |
| 4.2 | 19.4 | 0.8 | 19.7 | -0.3 |
| 5.0 | 17.6 | 0.8 | 17.2 | 0.4 |
| 5.8 | 15.9 | 0.7 | 15.6 | 0.3 |
| 7.0 | 14.1 | 0.6 | 14.0 | 0.1 |
| 8.2 | 12.9 | 0.6 | 13.0 | -0.1 |
| 9.4 | 12.2 | 0.6 | 12.3 | -0.1 |
| 10.6 | 11.3 | 0.5 | 11.7 | -0.4 |
| 11.8 | 11.0 | 0.5 | 11.3 | -0.3 |
| 13.2 | 10.8 | 0.5 | 10.9 | -0.1 |
| 14.8 | 10.8 | 0.6 | 10.5 | 0.3 |
| 16.4 | 10.7 | 0.7 | 10.2 | 0.5 |
| 18.0 | 10.3 | 0.5 | 10.0 | 0.3 |
| 22.2 | 9.0 | 0.5 | 9.46 | -0.5 |
| 36.8 | 7.8 | 0.5 | 8.40 | -0.6 |
| 77.1 | 7.25 | 0.5 | 7.28 | -0.03 |
| 87.0 | 7.2 | 0.5 | 7.11 | 0.09 |
The polarized emission component
![]() can be now obtained
from Eqs. (2) and (A12). For a simple model with constant magnetic
field one can obtain for the chromosphere and corona:
can be now obtained
from Eqs. (2) and (A12). For a simple model with constant magnetic
field one can obtain for the chromosphere and corona:
| (12) |
Copyright The European Southern Observatory (ESO)