In order to retrieve magnetic field from intensity and
polarization spectra emitted by an inhomogeneous solar atmosphere
we use the
radiation transfer equations for the Stoke's parameters of total intensity
![]() and
and
![]() for
circular polarization. These equations for the bremsstrahlung
emission mechanism in an inhomogeneous plane layered atmosphere
(see Appendix A) are:
for
circular polarization. These equations for the bremsstrahlung
emission mechanism in an inhomogeneous plane layered atmosphere
(see Appendix A) are:
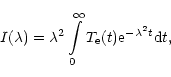 |
(1) |
| = | 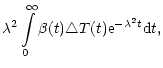 |
||
| = | 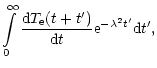 |
(2) |
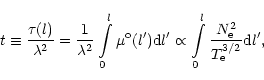 |
(3) |
The solution of the inverse problem given by Eqs. (1), (2) gives
the magnetic field
![]() and the
electron temperature
and the
electron temperature
![]() in the solar atmosphere as
functions of t. We call such solutions "tomographic" models
(see Bogod & Grebinskij [1997]) because they represent the only
direct information, which may be extracted from brightness spectra
without additional assumptions. The "physical" models, i.e.
spatial distributions of the electron number density
in the solar atmosphere as
functions of t. We call such solutions "tomographic" models
(see Bogod & Grebinskij [1997]) because they represent the only
direct information, which may be extracted from brightness spectra
without additional assumptions. The "physical" models, i.e.
spatial distributions of the electron number density
![]() ,
electron temperature
,
electron temperature
![]() and field B(h), may be retrieved
from the tomographic models by solving the inversion problem Eq.
(3),
which requires the assumptions on the relation between
and field B(h), may be retrieved
from the tomographic models by solving the inversion problem Eq.
(3),
which requires the assumptions on the relation between
![]() and
and
![]() .
This approach is quite
different from the standard model method
which starts with the information obtained from optical
observations and then does forward calculations to fit microwave observations
in the following steps:
.
This approach is quite
different from the standard model method
which starts with the information obtained from optical
observations and then does forward calculations to fit microwave observations
in the following steps:
![]() ,
,
![]() (see Avrett [1997] for review).
(see Avrett [1997] for review).
It was shown by Bogod & Grebinskij ([1997]), that Eq. (1) may
be effectively inverted to find
![]() by the differential
deconvolution method (DDM). However, that technique is not
applicable to Eq. (2), which cannot be reduced to a Laplace
transform. Thus, to retrieve magnetic fields from spectral
observations, we should use some estimates, well known from
previous studies by Bogod & Gelfreikh ([1980]) in the form of (see
Appendix A):
by the differential
deconvolution method (DDM). However, that technique is not
applicable to Eq. (2), which cannot be reduced to a Laplace
transform. Thus, to retrieve magnetic fields from spectral
observations, we should use some estimates, well known from
previous studies by Bogod & Gelfreikh ([1980]) in the form of (see
Appendix A):
![\begin{displaymath}\lbrack \beta (\lambda )]=\frac{V_{\rm obs}(\lambda )}{\lambd...
...\rm G}\equiv \frac{5350}{\lambda
_{\rm cm}}[\beta (\lambda )].
\end{displaymath}](/articles/aas/full/2000/10/ds8262/img46.gif) |
(4) |
In
order to obtain such estimates from observations of solar
atmosphere emission in the case of inhomogeneous magnetic fields,
one should answer on two questions: (i) Which layer of the
atmosphere (corona or chromosphere) gives the main contribution to
the polarization at a given wavelength ![]() ?
(ii) What is the relation between the estimated magnetic field [
?
(ii) What is the relation between the estimated magnetic field [
![]() ] (Eq. 4) and its real value in the case of an inhomogeneous field
B(h)?
] (Eq. 4) and its real value in the case of an inhomogeneous field
B(h)?
In order to answer these questions, we use a priori information about the distribution of temperature in the solar atmosphere, which may be extracted from observed brightness spectra by Eq. (1) and modelling.
Copyright The European Southern Observatory (ESO)