

Up: Characterization of adaptive optics
Subsections
5 Application to stellar field post-processing
One of the first applications of wide FOV imaging in astronomy is
the observation of large stellar fields. In this case, we have a strong a priori
information on the object: it is a sum of Dirac functions
[Gunsay & Jeffs1995,Fusco et al.1999b]:
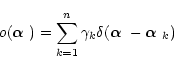 |
(17) |
where
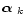 and
and 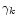 are the position vector and the intensity of
the
are the position vector and the intensity of
the
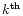 star respectively. They are the object parameters we are seeking.
We consider that n, the number of stars, is a known parameter. Note that,
using appropriate prior statistics (Bernouilli Gaussian or Poisson-Gaussian for example),
it is possible to generalize the method and to incorporate n as an unknown of the problem.
star respectively. They are the object parameters we are seeking.
We consider that n, the number of stars, is a known parameter. Note that,
using appropriate prior statistics (Bernouilli Gaussian or Poisson-Gaussian for example),
it is possible to generalize the method and to incorporate n as an unknown of the problem.
To solve this inverse problem, i.e., estimate the unknowns
(
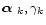 ), we use the approach presented in [Fusco et al.1999b]
with a isoplanatic PSF, but modified to include the anisoplanatic effects. Note that this appraoch can be seen as a "PSF
fitting'' in the Fourier domain.
), we use the approach presented in [Fusco et al.1999b]
with a isoplanatic PSF, but modified to include the anisoplanatic effects. Note that this appraoch can be seen as a "PSF
fitting'' in the Fourier domain.
The criterion to be minimized with respect to 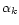 and
and
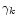 can be written in the Fourier domain as:
can be written in the Fourier domain as:
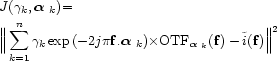 |
(18) |
where
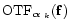 is the OTF for the
is the OTF for the
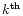 star and
star and
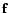 the spatial frequency and
the spatial frequency and 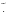 denotes a Fourier transform.
denotes a Fourier transform.
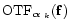 is slowly variable with
is slowly variable with 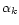 .
Then a
crude estimation of
.
Then a
crude estimation of 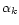 using a first deconvolution with a constant
PSF in the whole field of view allows the calculation of the associated ATF's.
In a first approximation, these ATF estimates are assumed to be the true ones
and are not adjusted in the deconvolution process. The criterion to be
minimized is then:
using a first deconvolution with a constant
PSF in the whole field of view allows the calculation of the associated ATF's.
In a first approximation, these ATF estimates are assumed to be the true ones
and are not adjusted in the deconvolution process. The criterion to be
minimized is then:
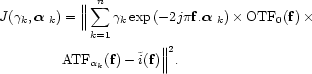 |
(19) |
Note that a more complete, but more complex approach should consider
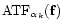 as unknow of the problem.
as unknow of the problem.
This minimization is done using a conjugate gradient method. The object
reparametrization allows an accurate precision on the parameters (sub-pixel
precision on the star positions). Nevertheless, the criterion is not convex and a good first initialization for the star positions is suitable to
avoid problems related to local minima. This initialization is made
using a pixel by pixel deconvolution (Wiener filter or Lucy Richardson
Algorithm for example).
Let us consider an object which is a field of 21 stars with the same magnitude.
The separation between each stars is one arcsecond (see Fig. 1).
In order to focus on the limitation induced by the anisoplanatic problem and
the gain brought by the ATF estimation, we first consider a noise free image,
but the noise influence will be discussed later in the paper.
We compare, on a noise free image (see Fig. 1), the gain brought
by the ATF introduction in the image processing. ATF's for each star are computed using
an estimation of 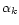 given by the first pixel by pixel deconvolution
(Wiener filter).
given by the first pixel by pixel deconvolution
(Wiener filter).
 is simply given by the fourier transform of the
on-axis PSF. We plot in Fig.
7 the error, given in percent, on the stars magnitude
estimate using "isoplanatic'' deconvolution process (deconvolution using
criterion defined in Eq. (18) but assuming that the PSF is
constant in the whole FOV) and our modified approach using the ATF estimation
for each star position Eq. (19).
Figure 7 shows the gain brought by the use of the ATF
in the a posteriori processing. The error, which increases as a function
of angle, in the "isoplanatic'' deconvolution case, up to 34% for
is simply given by the fourier transform of the
on-axis PSF. We plot in Fig.
7 the error, given in percent, on the stars magnitude
estimate using "isoplanatic'' deconvolution process (deconvolution using
criterion defined in Eq. (18) but assuming that the PSF is
constant in the whole FOV) and our modified approach using the ATF estimation
for each star position Eq. (19).
Figure 7 shows the gain brought by the use of the ATF
in the a posteriori processing. The error, which increases as a function
of angle, in the "isoplanatic'' deconvolution case, up to 34% for
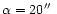 ,
is
close to be constant and only about 1% when we use the ATF estimation. We
believe that this
residual error is due to the non-stationarity assumption made in the ATF
estimation (see Sect. 3.3).
,
is
close to be constant and only about 1% when we use the ATF estimation. We
believe that this
residual error is due to the non-stationarity assumption made in the ATF
estimation (see Sect. 3.3).
![\begin{figure}\includegraphics[width=8cm]{ds1812f10.eps}\par\end{figure}](/articles/aas/full/2000/04/ds1812/Timg82.gif) |
Figure 7:
Error in percent on the magnitude estimation for each star in the
case of a noise free image.[ ]
estimation using the same PSF
( ]
estimation using the same PSF
(
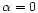 )
for the whole FOV, [*] estimation using the ATF associated to
each star )
for the whole FOV, [*] estimation using the ATF associated to
each star |
Of course, in a realistic case, the image is not only degraded by the
turbulence effect but also affected by photon and detector noise. Let us assume
that in the case of AO long exposures, the dominant noise is the photon noise.
It leads to an error on the parameter estimation.
In the case of a
"isoplanatic'' deconvolution (PSF constant in the whole FOV), for a given
flux (that is for a given noise level), a limit angle can be defined below which the anisoplanatic
error is lower than the noise error. The lower the flux,
the greater the limit angle (see Fig. 8). For
example, in the case of 103 photons the anisoplanatic error becomes greater
than the noise error for
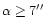 .
This limit
angle can be seen as a definition of an isoplanatic angle for our
deconvolution method.
.
This limit
angle can be seen as a definition of an isoplanatic angle for our
deconvolution method.
![\begin{figure}\includegraphics[width=8cm]{ds1812f11.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg84.gif) |
Figure 8:
Error in percent on the magnitude estimation using the same OTF
(
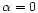 )
in the whole FOV, in the
case of a noise free image, and in the case of photon noise with
106, 105, 104 and
103 photons in the whole image respectively. The error is only averaged on 10
noise outcomes for each flux case )
in the whole FOV, in the
case of a noise free image, and in the case of photon noise with
106, 105, 104 and
103 photons in the whole image respectively. The error is only averaged on 10
noise outcomes for each flux case |
Now, let us use the ATF correction of the OTF in the post-processing. In that case, the noise error is dominant for the
whole FOV, as soon as it is of the order or greater than 1% which corresponds
to 105 photons in our
case (see Fig. 9).
![\begin{figure}\includegraphics[width=8cm]{ds1812f12.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg85.gif) |
Figure 9:
Error in percent on the magnitude estimation using the ATF correction
of the OTF
in the post processing in the
case of a noise free image, and in the case of photon noise with 106, 105 and
103 photons in the whole image respectively. The error is only averaged on 10
noise outcomes for each flux case |
Even if the ATF under-estimation
due to the phase non-stationarity error is the dominant noise for a flux
greater than 105 photons, the gain brought by the use of the ATF is still
very important with respect to a "isoplanatic'' deconvolution (see Figs.
8 and 9). And,
at low flux, the error in the FOV is only limited by the photon noise.
Let us now apply the wide FOV deconvolution method (Eq. 19) on the two experimental images of
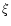 Cephee and
Cephee and  Orionis presented in Sect. 4. In these two cases, because of the large angular
separation between the two components, an accurate
estimation of the magnitude difference and of the separation can be obtained
using the sole images and computing a center of gravity and an integral of
the flux for each image. Since we have a good estimation of the
parameters of interest by this aperture photometry method, it is interesting to
validate our deconvolution approach on this data and to evaluate the gain
brought by the ATF estimation.
Orionis presented in Sect. 4. In these two cases, because of the large angular
separation between the two components, an accurate
estimation of the magnitude difference and of the separation can be obtained
using the sole images and computing a center of gravity and an integral of
the flux for each image. Since we have a good estimation of the
parameters of interest by this aperture photometry method, it is interesting to
validate our deconvolution approach on this data and to evaluate the gain
brought by the ATF estimation.
The results of the estimation of the separations and the magnitude differences
are summarized in Table 3 for each processing case:
-
- - a crude aperture photometry for the magnitude
estimation plus a center of gravity estimation for the seperation estimation;
-
- - a deconvolution with
a sole PSF (on axis PSF, that is the brighter star image) for the whole image
("isoplanatic'' deconvolution);
-
- - and the use of the ATF model in the
deconvolution process.
These results clearly show the gain brought by the ATF correction of the OTF on the
estimation of star parameters: mainly on the magnitude estimation. The
"isoplanatic'' deconvolution process, which is not
efficient in the case of large FOV, because of the PSF variation, is strongly
improved by the introduction of the theoretical degradation of this PSF as a
function of angle.


Up: Characterization of adaptive optics
Copyright The European Southern Observatory (ESO)
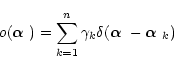
![]() and
and
![]() can be written in the Fourier domain as:
can be written in the Fourier domain as:
![]() .
This limit
angle can be seen as a definition of an isoplanatic angle for our
deconvolution method.
.
This limit
angle can be seen as a definition of an isoplanatic angle for our
deconvolution method.