

Up: Characterization of adaptive optics
Subsections
4 Experimental results
The theoretical estimation of OTF angular variation is compared with experimental data recorded in September
1997 with the ONERA adaptive optics bench installed on the 1.52 m telescope
at the Observatoire de Haute Provence [Conan et al.1998a]. The Adaptive Optics
Bench (BOA) is a 88 actuator system, with a Shack-Hartmann
wave-front sensor (64 sub-apertures). Two images of two separated binary
stars (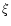 Cephee and
Cephee and  Orionis) were acquired at 850 nm, with a 10 second integration time, on the 29
September 1997 at 00 h 02 and 04 h 27 (UT). The visual magnitude of the two
components are: 4.6, 6.5 for
Orionis) were acquired at 850 nm, with a 10 second integration time, on the 29
September 1997 at 00 h 02 and 04 h 27 (UT). The visual magnitude of the two
components are: 4.6, 6.5 for 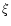 Chepee and 5.1, 6.7 for
Chepee and 5.1, 6.7 for
 Orionis. The separation of these binary stars is
large enough (about 8 and 13 arcsec) to obtain two PSF's with no
overlap (see Fig. 4). In each case, the brightest
star is used for the wave-front sensing.
During the same night at 21 h 21 (UT), a
Orionis. The separation of these binary stars is
large enough (about 8 and 13 arcsec) to obtain two PSF's with no
overlap (see Fig. 4). In each case, the brightest
star is used for the wave-front sensing.
During the same night at 21 h 21 (UT), a 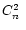 profile measurement was obtained
by M. Azouit from Université de Nice (France) (see Fig.
5) using balloon probes [Vernin & Munoz-Tunón1992].
For the two images the observing conditions are summarized in Table 1.
r0 has been estimated using open-loop Shack Hartmann data recorded shortly
before the corrected images and
profile measurement was obtained
by M. Azouit from Université de Nice (France) (see Fig.
5) using balloon probes [Vernin & Munoz-Tunón1992].
For the two images the observing conditions are summarized in Table 1.
r0 has been estimated using open-loop Shack Hartmann data recorded shortly
before the corrected images and 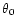 has been computed using r0, measured
has been computed using r0, measured 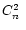 profile and
Eq. (16).
profile and
Eq. (16).
![\begin{figure}
\begin{tabular}{cc}
\includegraphics[width=4.1cm]{ds1812f5.eps} &\includegraphics[width=4.1cm]{ds1812f6.eps}\\
a & b \\
\end{tabular}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg59.gif) |
Figure 4:
Images of the two components of: a) 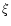 Cephee (separation Cephee (separation
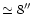 )
b) )
b)
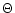 Orionis (separation Orionis (separation
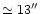 ). 1 pixel =0.027 arcsec,
image size = ). 1 pixel =0.027 arcsec,
image size = 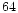 pixels
pixels |
We have approximated
this 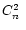 profile by 3 "equivalent layers'' (EL) [Fusco et al.1999a]. The true
profile by 3 "equivalent layers'' (EL) [Fusco et al.1999a]. The true
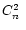 profile is divided in 3 slabs
(0 to 1 km, 1 to 10 km and 10 to 27 km), for each slab an EL is
located at an equivalent height defined as the weighted mean height of the
slab:
profile is divided in 3 slabs
(0 to 1 km, 1 to 10 km and 10 to 27 km), for each slab an EL is
located at an equivalent height defined as the weighted mean height of the
slab:
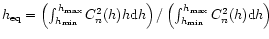 and with an associated
strength
given by the total strength of the slab
and with an associated
strength
given by the total strength of the slab
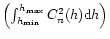 .
All the values are summarized in Table 2.
.
All the values are summarized in Table 2.
Table 2:
Results of the equivalent layer calculations
| |
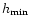 |
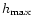 |
equivalent |
equivalent |
| |
|
|
height |
strength |
| |
(in km) |
(in km) |
(in km) |
(in %) |
| layer 1 |
0 |
1 |
7.7 |
56.5 |
| layer 2 |
1 |
10 |
3.3 |
33.5 |
| layer 3 |
10 |
27 |
14.1 |
10 |
Because of the weak dependency of the angular decorrelation
of the phase with the atmospheric profile, this  approximation is enough to
obtain a good estimate on the phase angular decorrelation. We checked that an increase of the layer number (three to one hundred) do
not significantly change the results.
approximation is enough to
obtain a good estimate on the phase angular decorrelation. We checked that an increase of the layer number (three to one hundred) do
not significantly change the results.
![\begin{figure}
\includegraphics[width=8cm]{ds1812f7.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg64.gif) |
Figure 5:
 profile measurements obtained with balloon probes by
M. Azouit [solid line] and position of the 3 equivalent layers [dashed line] profile measurements obtained with balloon probes by
M. Azouit [solid line] and position of the 3 equivalent layers [dashed line] |
In order to estimate the OTF, the AO system is assumed to provide a perfect
correction of a given number of Zernike polynomials. This number N is defined so that the Nfirst modes have a wavefront reconstruction SNR higher than 1. For this
purpose, we use the theoretical behavior of the turbulent and of the
noise variance [Rigaut & Gendron1992]. These variances are scaled using the
measured values of r0 and L0 for the Zernike turbulent variance and by the
propagation of the photon and detector noise in the wavefront sensor through
the reconstruction matrix for the Zernike noise variance [Rousset1999].
With the observing conditions, the correction in terms of Zernike polynomials is
efficient (SNR 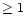 )
about up to the
)
about up to the
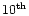 Zernike for
Zernike for 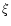 Cephee and the
Cephee and the
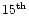 Zernike for
Zernike for 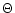 Orionis.
Orionis.
Now, we compute the OTF for each binary star component
(Eq. 7): the theoretical ATF is given by Eqs. (12)
and (8) using:
-
- - the 3 EL's
profile for the computation of the angular correlation of the Zernike;
-
- - the first
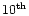 (resp.
(resp.
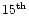 )
Zernike coefficients;
)
Zernike coefficients;
-
- - the known separation
between the two stars.
The on-axis OTF is given by the first component of each binary star (brightest star).
The comparison between
the measured OTF and the computed OTF is shown in Fig. 6.
![\begin{figure}\par\includegraphics[width=8cm]{ds1812f8.eps}\\
\includegraphics[width=8cm]{ds1812f9.eps}\\
\par\end{figure}](/articles/aas/full/2000/04/ds1812/Timg68.gif) |
Figure 6:
Comparison between the measured [dashed line] and the computed [solid
line] off-axis OTF.
The measured OTF for  (brightest star) [dotted-dashed line] is given for comparison:
(top)
(brightest star) [dotted-dashed line] is given for comparison:
(top) 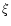 Cephee and (bottom) Cephee and (bottom) 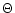 Orionis. The circular average of each OTF
is plotted Orionis. The circular average of each OTF
is plotted |
In the two cases, a good accordance between measured and computed OTF is found
although a large number of assumptions has been made to compute the ATF:
-
- -
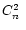 constant during the whole night (3h 40mn and 8h between the
constant during the whole night (3h 40mn and 8h between the
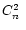 measurement and the two observations). Even if we know that the
sensitivity to this profile is low;
measurement and the two observations). Even if we know that the
sensitivity to this profile is low;
-
- - r0 and L0 estimation from the WFS noisy
data assumed to be perfect;
-
- - efficient correction of respectively the first 10 and 15 Zernike
coefficients, which is a crude approximation of the AO system.
These results are very encouraging and allow to be optimistic for large FOV
image post-processing.
Now, let us use the theoretical model of the PSF degradation for the
post-processing of AO wide FOV images of stellar fields.


Up: Characterization of adaptive optics
Copyright The European Southern Observatory (ESO)
![]() approximation is enough to
obtain a good estimate on the phase angular decorrelation. We checked that an increase of the layer number (three to one hundred) do
not significantly change the results.
approximation is enough to
obtain a good estimate on the phase angular decorrelation. We checked that an increase of the layer number (three to one hundred) do
not significantly change the results.
![\begin{figure}
\includegraphics[width=8cm]{ds1812f7.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg64.gif)
![]() )
about up to the
)
about up to the
![]() Zernike for
Zernike for ![]() Cephee and the
Cephee and the
![]() Zernike for
Zernike for ![]() Orionis.
Orionis.