

Up: Characterization of adaptive optics
Subsections
3 Comparison between theory and simulation
In order to validate the Eqs. (5) and (12) derived in Sect. 2,
wide FOV AO images are simulated. We consider a three layer 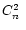 profile: one on the pupil, the second at one km and the third at ten km with
respectively 20, 60 and 20% of the turbulence. Using the so-called near-field approximation [Roddier1981], the scintillation effects are
neglected and the phase on the telescope pupil for a given direction
profile: one on the pupil, the second at one km and the third at ten km with
respectively 20, 60 and 20% of the turbulence. Using the so-called near-field approximation [Roddier1981], the scintillation effects are
neglected and the phase on the telescope pupil for a given direction
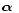 is simply the sum of the corresponding part of each phase screen in each turbulent layer:
is simply the sum of the corresponding part of each phase screen in each turbulent layer:
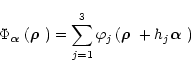 |
(15) |
where 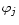 and hj are respectively the phase screen and the height
of the
and hj are respectively the phase screen and the height
of the
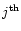 layer. Each phase screen is simulated by N. Roddier's
method [Roddier1990] using the 861 first Zernike polynomials (radial order
up to 40). The size of these phase screens corresponds to a 20 arcsecs
FOV radius and a telescope diameter of 4 m. The overall D/r0 is 10.
layer. Each phase screen is simulated by N. Roddier's
method [Roddier1990] using the 861 first Zernike polynomials (radial order
up to 40). The size of these phase screens corresponds to a 20 arcsecs
FOV radius and a telescope diameter of 4 m. The overall D/r0 is 10.
Let us consider an
adaptive optics system which can perfectly correct the i0 first Zernike
polynomials, in our case, i0=21. We have simulated a PSF at every arcsecond in the FOV (20
arcsec). Each PSF is the sum of 1000 time-decorrelated short exposures which
are deduced from
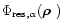 .
If we consider that the speckle
lifetime is about 10 ms, the simulation are roughly equivalent to a 10 s
long exposure.
Figure 1 shows the PSF evolution as a function
of angle. Note that the PSF does not vary significantly within 3
arcsec, which roughly corresponds to the isoplanatic angle given by
Roddier Roddier-81a:
.
If we consider that the speckle
lifetime is about 10 ms, the simulation are roughly equivalent to a 10 s
long exposure.
Figure 1 shows the PSF evolution as a function
of angle. Note that the PSF does not vary significantly within 3
arcsec, which roughly corresponds to the isoplanatic angle given by
Roddier Roddier-81a:
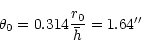 |
(16) |
with 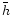 given by [Fried1982]
given by [Fried1982]
In this field, the PSF
variations are only due to the turbulence noise (finite number of short
exposures in the PSF calculation).
![\begin{figure}
\begin{tabular}{c}
\includegraphics[width=8cm]{ds1812f1.eps}\\
\includegraphics[width=8.55cm]{ds1812f2.eps}\end{tabular}\par\end{figure}](/articles/aas/full/2000/04/ds1812/Timg52.gif) |
Figure 1:
PSF in the FOV versus angle. On the top: 2D images of the
simulated PSF's for each arcsecond. On the bottom:X-cut of the images. The
PSF's normalized by the diffraction (in percent) |
Outside the isoplanatic field, the PSF degradation is
important, the Strehl Ratio goes from 43% at the center of the field to less than 10%
at the border of the field. Of course, a deconvolution scheme, assuming
that the PSF is constant in the whole field of view, would lead to a poor
restoration. Note that the non-circularity of the off-axis PSF's appears in
Fig. 1.
3.3 Results
For each angle, we compare the theoretical OTF (see Eqs.
7 and 8) to
the simulated one.
A very
good estimation for each OTF is obtained, even in the case of large values of
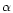 (see Fig. 2).
(see Fig. 2).
![\begin{figure}
\includegraphics[width=8cm]{ds1812f3.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg54.gif) |
Figure 2:
Y-cut of the simulated OTF (dashed line) and theoretical OTF given by
Eq. (7) (solid line) for
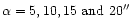 .
The OTF for .
The OTF for 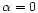 is shown for
comparison
is shown for
comparison |
Because we only consider a Y-cut of the OTF's in Fig. 2,
the anisotropic (elongation) effect is not visible. In Fig.
3 we only consider one angle (
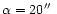 )
but we plot two cuts (X and Y axis) of the simulated and theoretical OTF. In that case, the anisotropic effect and its good restitution by the analytical ATF
is shown.
)
but we plot two cuts (X and Y axis) of the simulated and theoretical OTF. In that case, the anisotropic effect and its good restitution by the analytical ATF
is shown.
A small under-estimation of the OTF can be seen in each case with the
analytical method. The difference between the simulated and theoretical OTF's
is due to the phase non-stationarity error. In Sect. 2 we
have assumed the phase stationarity on the telescope pupil. This
assumption corresponds to approximate the mean of the exponential of
function by the exponential of the mean of the function. Even if this
approximation is quite good [Véran1997], it leads, nevertheless, to a
small under estimation of the theoretical OTF.
This error gives the fundamental limitation of the method, but in experimental data
processing, other error sources may also degrade the results, such as:
![\begin{figure}
\includegraphics[width=8cm]{ds1812f4.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg56.gif) |
Figure 3:
Y-cut and X-cut of the simulated OTF (dashed line) and the
theoretical OTF (solid line) for
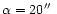 |
- - atmospheric parameter estimation errors on: r0, L0, Cn2 profile;
-
- - AO full correction of the first
Zernike modes which is only an approximation of a real system;
-
- - turbulent noise: finite exposure time which leads to a
residual speckle pattern in the long exposure image.
But we show in the next section, that in a real case, all these errors do not
significantly influence the ATF estimation.


Up: Characterization of adaptive optics
Copyright The European Southern Observatory (ESO)
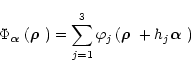
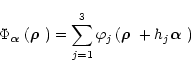
![\begin{displaymath}\bar{h} = \left [\frac{\int_0^{\infty}h^{\frac{5}{3}}C_n^2(h)...
..._0^{\infty}C_n^2(h) {\rm d}h}\right ]^{\frac{3}{5}} = 3953 m .
\end{displaymath}](/articles/aas/full/2000/04/ds1812/img51.gif)
![\begin{figure}
\begin{tabular}{c}
\includegraphics[width=8cm]{ds1812f1.eps}\\
\includegraphics[width=8.55cm]{ds1812f2.eps}\end{tabular}\par\end{figure}](/articles/aas/full/2000/04/ds1812/Timg52.gif)
![\begin{figure}
\includegraphics[width=8cm]{ds1812f3.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg54.gif)
![]() )
but we plot two cuts (X and Y axis) of the simulated and theoretical OTF. In that case, the anisotropic effect and its good restitution by the analytical ATF
is shown.
)
but we plot two cuts (X and Y axis) of the simulated and theoretical OTF. In that case, the anisotropic effect and its good restitution by the analytical ATF
is shown.
![\begin{figure}
\includegraphics[width=8cm]{ds1812f4.eps}\end{figure}](/articles/aas/full/2000/04/ds1812/Timg56.gif)