In this section, we review the basic physics of radiative driving of an ensemble of lines and interpret the final outcome in terms of a so-called "line-strength distribution function''. To this end, we allow for a number of approximations which will turn out to be of either minor importance or will be relaxed during further proceedings. Specifically,
where
![]() is the number of photospherically emitted photons
per unit time in the frequency range
is the number of photospherically emitted photons
per unit time in the frequency range
![]() ,
,
![]() the stellar luminosity and
the stellar luminosity and
| = | 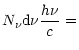 |
||
| = | 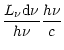 |
(2) |
the average transferred momentum by line absorption or scattering (radially streaming photons provided and accounting for the cancellation of the foreaft-symmetric reemission processes). Finally,
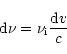 |
(3) |
is the frequency range which can actually contribute to line scattering
inside the shell via the Doppler effect, and
![]() is the interaction probability for a line optical depth
(in Sobolev approximation)
is the interaction probability for a line optical depth
(in Sobolev approximation)
To proceed further, we have to sum up the contribution of all individual lines to obtain the total radiative acceleration. To this end, we define the dimensionless line-strength of a single line as
![]() is the Thomson scattering opacity,
is the Thomson scattering opacity,
![]() the
Doppler width of the line and
the
Doppler width of the line and
![]() the ionic thermal velocity. From
Eq. (6), the line-strength can be interpreted twofold. On the one
side, it is, except from a factor
the ionic thermal velocity. From
Eq. (6), the line-strength can be interpreted twofold. On the one
side, it is, except from a factor
![]() ,
the maximum opacity of the
considered line in units of the minimum continuum opacity present in the
wind (=Thomson). Alternatively, it can be considered, except a factor of
,
the maximum opacity of the
considered line in units of the minimum continuum opacity present in the
wind (=Thomson). Alternatively, it can be considered, except a factor of
![]() ,
as the ratio of frequency integrated line opacity
,
as the ratio of frequency integrated line opacity
![]() to minimum frequency integrated continuum opacity
to minimum frequency integrated continuum opacity
![]() .
.
One comment is necessary here: The incidence of
![]() at this stage of
reasoning seems to be "natural'' in terms of understanding the physical
meaning of line-strength. Moreover, it is actually needed if we require the
latter to be dimensionless, which is important for our future statistical
analysis. As it will turn out, however,
at this stage of
reasoning seems to be "natural'' in terms of understanding the physical
meaning of line-strength. Moreover, it is actually needed if we require the
latter to be dimensionless, which is important for our future statistical
analysis. As it will turn out, however,
![]() will reappear in various
combinations with other quantities after summing up the line-strength
contributions of different metals, i.e.,
will reappear in various
combinations with other quantities after summing up the line-strength
contributions of different metals, i.e.,
![]() would be no longer unique
due to its dependence on atomic mass. Thus, from now on we will concentrate
on the most important aspect of
would be no longer unique
due to its dependence on atomic mass. Thus, from now on we will concentrate
on the most important aspect of
![]() in this context, namely that it
has a dimension (also noting that its value is smaller than the
sound-speed), however use a value independent of atomic mass, in particular,
the value for hydrogen.
in this context, namely that it
has a dimension (also noting that its value is smaller than the
sound-speed), however use a value independent of atomic mass, in particular,
the value for hydrogen.
The relation of the so defined line-strength to Sobolev optical depth is given by
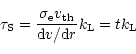 |
(7) |
where t is the optical depth parameter defined by CAK. The advantage of
using ![]() instead of opacities or optical depths is that
instead of opacities or optical depths is that ![]() is a
quantity which remains rather constant throughout the wind (at least in the
typical case of frozen-in ionization), and whose distribution can be
described in an almost depth independent statistical way. Before doing this,
however, we will sum up the contributions of all individual lines, in the
spirit outlined above, i.e., by dividing lines into two categories.
Optically thick lines are those with
is a
quantity which remains rather constant throughout the wind (at least in the
typical case of frozen-in ionization), and whose distribution can be
described in an almost depth independent statistical way. Before doing this,
however, we will sum up the contributions of all individual lines, in the
spirit outlined above, i.e., by dividing lines into two categories.
Optically thick lines are those with
![]() and interaction
probability "1'', whereas optically thin lines shall have
and interaction
probability "1'', whereas optically thin lines shall have
![]() and
interaction probability
and
interaction probability
![]() .
Defining
.
Defining
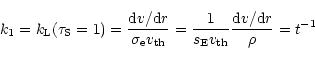 |
(8) |
as the line-strength where the division
![]() is reached, we find for
the total line acceleration
is reached, we find for
the total line acceleration
The first term inside the bracket gives the contribution by optically
thick lines and depends only on the hydrodynamical structure via
![]() ,
whereas the second term gives the optically thin line
contribution and is independent of the hydro-structure, however depends on
the specific line-strengths, i.e., atomic properties and level population.
,
whereas the second term gives the optically thin line
contribution and is independent of the hydro-structure, however depends on
the specific line-strengths, i.e., atomic properties and level population.
Before going into further detail and in concert with most previous
investigations related to this topic, we will assume that the number of
lines in a frequency interval
![]() and line-strength
and line-strength
![]() can be represented by a power-law
can be represented by a power-law
with
![]() ,
where the frequential distribution shall be independent from the line-strength distribution. The negative sign accounts
for the fact that the number of lines increases for decreasing
line-strength. So far, the normalization "constant''
,
where the frequential distribution shall be independent from the line-strength distribution. The negative sign accounts
for the fact that the number of lines increases for decreasing
line-strength. So far, the normalization "constant'' ![]() is allowed to
have some additional depth dependence. With (10) and substituting
the sums in (9) by appropriate (double-) integrals with
frequencies from
is allowed to
have some additional depth dependence. With (10) and substituting
the sums in (9) by appropriate (double-) integrals with
frequencies from
![]() and line-strengths from
and line-strengths from
![]() and
and
![]() ,
respectively, we find
,
respectively, we find
Note, that in case of
![]() the contribution from optically thin
lines (second term) would diverge at its lower boundary. From
Eq. (12), two points are obvious: Both the line-force provided
by optically thick and by optically thin lines scales with the same power
the contribution from optically thin
lines (second term) would diverge at its lower boundary. From
Eq. (12), two points are obvious: Both the line-force provided
by optically thick and by optically thin lines scales with the same power
![]() ,
and we can interpret this exponent as the ratio of line-force from
optically thick lines to total force,
,
and we can interpret this exponent as the ratio of line-force from
optically thick lines to total force,
a result, which we will later on discuss carefully. Collecting terms and using the radiative acceleration provided by Thomson-scattering as a scaling factor,
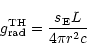 |
(14) |
with stellar luminosity L, we can express the total line acceleration in terms of the so-called force-multiplier f.m.(r),
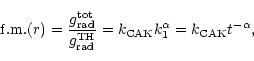 |
(15) |
where the force-multiplier parameter
![]() is defined by
is defined by
This result was given firstly by CAK. Note, however, that they additionally
assumed
![]() ,
in which case the first
factor in (16) is unity.
,
in which case the first
factor in (16) is unity.
The first equation above can be interpreted as the product of the radiative
acceleration if the line were optically thin, multiplied by the
correction for self-shadowing due to the actual optical depth
![]() (cf.
also Gayley [1995]). Integrating over the line-strength distribution
function without performing the division at
(cf.
also Gayley [1995]). Integrating over the line-strength distribution
function without performing the division at
![]() ,
we obtain
directly the "exact'' version of Eq. (12),
,
we obtain
directly the "exact'' version of Eq. (12),
with Gamma-function
![]() .
Thus, since
.
Thus, since
![]() (by
assumption), the error introduced by our approximation is given by
(by
assumption), the error introduced by our approximation is given by
![]() ,
i.e., an overestimation of at most 13%.
,
i.e., an overestimation of at most 13%.
In the previous section, we have shown that the assumption of
power-law distributed line-strengths with exponent
![]() directly
leads to an ensemble line-force being proportional to
directly
leads to an ensemble line-force being proportional to
![]() ,
and that
in this case
,
and that
in this case ![]() turns out to represent the ratio of optically thick to
total line acceleration, provided that
turns out to represent the ratio of optically thick to
total line acceleration, provided that
![]() .
.
In so far, it seems quite natural to consider line strength distribution function and line force as interchangeable quantities and to identify the line-force exponent instantaneously as a manifestation of the underlying line-statistics. Although this perspective is widely spread, a closer inspection of the above procedure immediately necessitates a major caveat:
Due to the different weighting of line-strength in the expression for the
line-force (Eq. 11),
![]() and
and
![]() ,
a strict
correspondence between the exponent of line-strength distribution and
force-multiplier parameter can be expected a priori only if the distribution
follows a power-law over a large range of line-strengths. If the
distribution is curved in the log, this equality remains questionable and
has to be considered with caution, even if one accounts for locally
defined values
,
a strict
correspondence between the exponent of line-strength distribution and
force-multiplier parameter can be expected a priori only if the distribution
follows a power-law over a large range of line-strengths. If the
distribution is curved in the log, this equality remains questionable and
has to be considered with caution, even if one accounts for locally
defined values
![]() .
.
To investigate this problem, we consider a generalized line-strength distribution function
with arbitrary (positive) function
![]() ,
where we even allow for a
dependence of line-strength on frequency. Then, by realizing that
,
where we even allow for a
dependence of line-strength on frequency. Then, by realizing that
is the flux (times frequency) weighted cumulative number of lines stronger
than ![]() ,
we can integrate the optically thin contribution in
(11) by parts and obtain, after adding the optically thick
contribution
,
we can integrate the optically thin contribution in
(11) by parts and obtain, after adding the optically thick
contribution
Here we have assumed that the total (flux weighted) number of lines
![]() remains finite. (Actually, the much weaker requirement that
remains finite. (Actually, the much weaker requirement that
![]() for
for
![]() is sufficient.)
is sufficient.)
Equation (21) can be alternatively expressed as
with
![]() the weighted number of lines
stronger than
the weighted number of lines
stronger than ![]() (which are then optically thick by definition) and
(which are then optically thick by definition) and
![]() the cumulative number of optically thin lines (
the cumulative number of optically thin lines (
![]() ).
Figure 1 displays this result graphically. Note, that in order to
derive this result, we have again used our approximation of replacing
the interaction probability
).
Figure 1 displays this result graphically. Note, that in order to
derive this result, we have again used our approximation of replacing
the interaction probability
![]() by
by
![]() ,
respectively.
,
respectively.
Before we proceed further, let us mention that Eq. (22) and
Fig. 1 allow for an useful visualization of two extreme cases.
At first, assume that either the velocity gradient is so small or the
density so high that all lines are effectively stronger than/equal to ![]() .
In this optically thick case,
.
In this optically thick case, ![]() is situated in the left part of
the previous figure, and
is situated in the left part of
the previous figure, and
![]() for all
for all
![]() by definition (no lines weaker than
by definition (no lines weaker than ![]() present). The
acceleration is then found from the rectangular area between
present). The
acceleration is then found from the rectangular area between
![]() ,
i.e.,
,
i.e.,
![]() and thus
and thus
![]() .
From the
figure, it is also clear that the resulting acceleration is enormously
reduced compared to the case of all lines being optically thin (cf. also
Eq. (17)), which is the other extreme. In the latter case (arising
for large velocity gradients or low densities),
.
From the
figure, it is also clear that the resulting acceleration is enormously
reduced compared to the case of all lines being optically thin (cf. also
Eq. (17)), which is the other extreme. In the latter case (arising
for large velocity gradients or low densities), ![]() lies at the rightmost
point of the abscissa, and all lines have strengths lower than
lies at the rightmost
point of the abscissa, and all lines have strengths lower than ![]() .
Hence, the integral becomes independent of
.
Hence, the integral becomes independent of ![]() ,
and the radiative
acceleration obtains its maximum value with
,
and the radiative
acceleration obtains its maximum value with
![]() .
In all other
cases, the
.
In all other
cases, the ![]() -parameter of the line-force corresponds to the ratio of
"dark'' area (optically thick force) and the sum of light and dark
area (total force), cf. Eq. (13) for the case of a strict
power-law and Sect. 2.4 otherwise.
-parameter of the line-force corresponds to the ratio of
"dark'' area (optically thick force) and the sum of light and dark
area (total force), cf. Eq. (13) for the case of a strict
power-law and Sect. 2.4 otherwise.
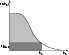 |
Figure 1: The line-force as integral of (flux weighted) cumulative line number over line-strength; contribution by optically thin (light) and optically thick lines (dark). Compare Eq. (22) and text |
On the basis of our alternative and general expression (21) for
the line-force, we can now answer the question raised above, namely under
which conditions this line-force can be represented by the CAK law
![]() ,
where
,
where ![]() corresponds at least to some local
exponent of our arbitrary line-strength distribution function.
corresponds at least to some local
exponent of our arbitrary line-strength distribution function.
To this end, we define two line-strengths
![]() ,
where k- and
k+ are chosen in such a way that
,
where k- and
k+ are chosen in such a way that
![]() follows roughly a power-law in
between, i.e., is roughly linear with slope
follows roughly a power-law in
between, i.e., is roughly linear with slope
![]() in the log-log
representation. Actually, this is almost always possible if the range
in the log-log
representation. Actually, this is almost always possible if the range
![]() is not too large, say of order two dex. (Here and in the
following we assume that the wind is not too thin, so that
is not too large, say of order two dex. (Here and in the
following we assume that the wind is not too thin, so that ![]() lies
well below the maximum line-strength.)
lies
well below the maximum line-strength.)
The number of lines at k+ is then N+, N- is N(k-) (flux weighting always provided, however brackets suppressed to simplify notation) and the distribution function in between can be approximated by
| = | |||
| = | 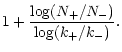 |
(23) |
Since by definition
![]() and
k+> k-, the maximum value
of
and
k+> k-, the maximum value
of ![]() is constrained to be unity, which occurs in those cases
when the maximum line number is reached at a certain
is constrained to be unity, which occurs in those cases
when the maximum line number is reached at a certain ![]() -value.
-value.
![]() -values below zero are not excluded from now on in our local
description.
-values below zero are not excluded from now on in our local
description.
Under these conditions and using (22), the total line acceleration is given by
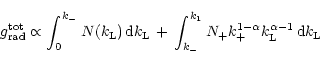
(
![]() ), where
), where
![]() is the appropriate average of
is the appropriate average of
![]() in the
range
in the
range
![]()
From Eq. (24), it is obvious that the ensemble line-force can be
represented by
![]() with local
with local ![]() ,
if and only if the
first term is small compared to the second one, where the former is just the
difference between actual and "fitted'' area (i.e., acceleration) in the
range
,
if and only if the
first term is small compared to the second one, where the former is just the
difference between actual and "fitted'' area (i.e., acceleration) in the
range
![]() .
.
In Appendix A, we show that under fairly general assumptions this is
actually the case if
![]() ,
i.e., as long as the local slope of
the flux-weighted cumulative line-strength distribution (in the log-log
representation) is larger than -1. In contrast, line distributions with a
steep slope over a large
,
i.e., as long as the local slope of
the flux-weighted cumulative line-strength distribution (in the log-log
representation) is larger than -1. In contrast, line distributions with a
steep slope over a large ![]() range will decouple from the line-force
parameterization (cf. also Sect. 4.2.8), leading to effective
range will decouple from the line-force
parameterization (cf. also Sect. 4.2.8), leading to effective ![]() values in the line-force (see below) different from those defining the
line-strength statistics.
values in the line-force (see below) different from those defining the
line-strength statistics.
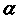
Usually, the force multiplier parameters are not derived from the
line-strength distribution function, however from the line-force itself,
i.e., accouting explicitely for the additional weighting with ![]() mentioned above.
mentioned above.
Thus, in the following we postulate the line force to be a function of
![]() with no a priori knowledge of
with no a priori knowledge of ![]() .
Instead, we define an
effective value
.
Instead, we define an
effective value
![]()
![]() by
by
From this definition and using ensemble line-forces calculated by
summing up their individual components (e.g., Abbott [1982];
Pauldrach et al. [1994]), we obtain by straightforward
differentiation (cf. Eq. 17)
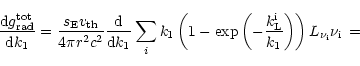
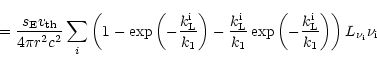
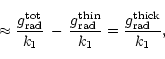 |
(27) |
where we have performed our approximation
![]() for
for
![]() ,
respectively, and neglected 2nd order terms.
Hence, from Eq. (26)
,
respectively, and neglected 2nd order terms.
Hence, from Eq. (26)
we find the same result as in Eq. (13), however independent
of any underlying line statistics! Especially, this result does not
rely on any separability of frequency and line-strength![]() .
.
In a first interpretation of
![]() ,
Abbott ([1980], his Eq. 10)
found a result different from our Eq. (28). This difference,
however, bases on Abbott's implicit assumption that the average
(flux times frequency weighted) line-strength of optically thin lines,
,
Abbott ([1980], his Eq. 10)
found a result different from our Eq. (28). This difference,
however, bases on Abbott's implicit assumption that the average
(flux times frequency weighted) line-strength of optically thin lines,
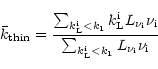 |
(29) |
does not depend on the hydro variable ![]() .
If one relaxes this assumption
and accounts also for the variation of
.
If one relaxes this assumption
and accounts also for the variation of
![]() as function of
as function of
![]() ,
the nominator in Abbott's Eq. (10) becomes unity and the same result
for
,
the nominator in Abbott's Eq. (10) becomes unity and the same result
for
![]() is recovered as given in (28).
is recovered as given in (28).
From this expression, it is obvious that
![]() must lie in the range
0...1. Combined with our previous notion that the line-force can be
parameterized in the form
must lie in the range
0...1. Combined with our previous notion that the line-force can be
parameterized in the form
![]() if the local
if the local ![]() value of the
distribution function is larger than zero, this leads to the result that we
should have
value of the
distribution function is larger than zero, this leads to the result that we
should have
![]() for a large range of
line-strengths as long as this condition is met. If the distribution has a
significant steepness locally,
for a large range of
line-strengths as long as this condition is met. If the distribution has a
significant steepness locally,
![]() is to be expected.
is to be expected.
Furthermore, the value of
![]() is independent of
is independent of ![]() if and only if
the flux-weighted line-strength distribution follows an exact power
law with exponent
if and only if
the flux-weighted line-strength distribution follows an exact power
law with exponent ![]() .
In this case then,
.
In this case then,
![]() globally. Otherwise,
globally. Otherwise,
![]() becomes a function of
becomes a function of ![]() and thus a
function of depth. An instructive example is given in Appendix B.
and thus a
function of depth. An instructive example is given in Appendix B.
 :
Acceleration vs. line-number
ratio
:
Acceleration vs. line-number
ratio
It has often been argued that
![]() is closely related to the number ratio of optically thick to thin lines, contrasted to the above
formulated acceleration ratio. In the following, however, we will show
that the former gives little (if any) insight into the behaviour of
is closely related to the number ratio of optically thick to thin lines, contrasted to the above
formulated acceleration ratio. In the following, however, we will show
that the former gives little (if any) insight into the behaviour of
![]() .
.
At first note that in view of Eq. (11) the optically thin line-force can be expressed by
| (30) |
Thus, the product of (flux weighted) number of optically thin lines times
average line-strength
![]() remains bounded,
although the number itself may formally diverge, e.g. for a typical
power-law index
remains bounded,
although the number itself may formally diverge, e.g. for a typical
power-law index
![]() .
In this case then, the average
line-strength of optically thin lines
.
In this case then, the average
line-strength of optically thin lines
![]() approaches zero!
approaches zero!
To avoid this possible divergence and also to keep the computational effort
as small as possible, one usually defines a minimum line-strength
![]() as a lower boundary for the contributing lines, resulting in a modified
acceleration
as a lower boundary for the contributing lines, resulting in a modified
acceleration
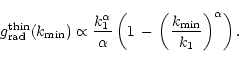 |
(31) |
Hence and under "normal'' conditions (
![]() ), it is
sufficient to account for lines stronger than
), it is
sufficient to account for lines stronger than
![]() ,
i.e., stronger
than Thomson-scattering, if one calculates the line-force (this was done,
e.g., in Fig. A1). However, in cases of high wind densities, this
limit has to be lowered, since the contribution of weaker lines with
,
i.e., stronger
than Thomson-scattering, if one calculates the line-force (this was done,
e.g., in Fig. A1). However, in cases of high wind densities, this
limit has to be lowered, since the contribution of weaker lines with
![]() becomes considerable then.
becomes considerable then.
Using this cutoff, the number ratio of optically thick to thin lines is given by
The latter limit, of course, is only valid for
![]() .
In consequence,
even for the simple picture of a perfect power-law, the "knowledge'' or
anticipated behaviour of
.
In consequence,
even for the simple picture of a perfect power-law, the "knowledge'' or
anticipated behaviour of
![]() gives only little (if any) insight
into the value of
gives only little (if any) insight
into the value of
![]() .
E.g., the expectation that
.
E.g., the expectation that
![]() implies
implies
![]() is, in view of Eq. (33), by
no means justified. As one example of this kind of misinterpretation, we
want to mention the argument given by Kudritzki et al.
([1987]) to explain the lower
is, in view of Eq. (33), by
no means justified. As one example of this kind of misinterpretation, we
want to mention the argument given by Kudritzki et al.
([1987]) to explain the lower
![]() -values resulting from
NLTE-calculations for winds with reduced metallicity. It was argued that
this effect can be "easily understood in terms of the metallicity'', since
the "ratio of strong to weak lines must decrease accordingly'' if the
metallicity is lowered. With respect to Eq. (33), this argument
is simply wrong, since the plain number ratio becomes inevitably smaller for
a reduced wind density (
-values resulting from
NLTE-calculations for winds with reduced metallicity. It was argued that
this effect can be "easily understood in terms of the metallicity'', since
the "ratio of strong to weak lines must decrease accordingly'' if the
metallicity is lowered. With respect to Eq. (33), this argument
is simply wrong, since the plain number ratio becomes inevitably smaller for
a reduced wind density (![]() larger) and thus cannot be used to give any
predictions concerning
larger) and thus cannot be used to give any
predictions concerning
![]() .
What really matters - if one prefers a
discussion in terms of line numbers - is the ratio of optically thick lines
to the average number of lines in the range
.
What really matters - if one prefers a
discussion in terms of line numbers - is the ratio of optically thick lines
to the average number of lines in the range
![]() ,
,
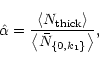 |
(35) |
As we have mentioned in the introduction, Gayley ([1995])
considered the problem of radiative line driving in a concept somewhat
different from the conventional approach. After discussing the physical
origin why radiative line driving is so much more efficient than the
radiative continuum acceleration, he introduces the meanwhile well known
quantity ![]() and relates it to the alternative modified CAK approach.
The reason that his approach seems to be somewhat favourable compared to the
latter is his finding that
and relates it to the alternative modified CAK approach.
The reason that his approach seems to be somewhat favourable compared to the
latter is his finding that ![]() should be much more constant than the
line-force parameter
should be much more constant than the
line-force parameter
![]() ,
which is somewhat messed up with implicit
dependencies on
,
which is somewhat messed up with implicit
dependencies on ![]() ,
cf. Eq. (16). By comparing with various
published values of force-multipliers, he concludes that
,
cf. Eq. (16). By comparing with various
published values of force-multipliers, he concludes that ![]() should be
of the order 1000 to 2000. In order to compare to his approach and since
in the remaining part of the paper we are mostly concerned with the
parameter
should be
of the order 1000 to 2000. In order to compare to his approach and since
in the remaining part of the paper we are mostly concerned with the
parameter ![]() ,
we will briefly relate his findings to our concept in
the following, and comment on some problems if one considers realistic
line-distribution functions in Sect. 3.3.
,
we will briefly relate his findings to our concept in
the following, and comment on some problems if one considers realistic
line-distribution functions in Sect. 3.3.
At first note that Gayley's line-strength parameter q relates to our definition as
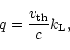 |
(36) |
where we have argued previously that in our notation
![]() is evaluated for
hydrogen, i.e., is temperature, however not mass dependent.
is evaluated for
hydrogen, i.e., is temperature, however not mass dependent.
Similarly, Gayley's cutoff parameter ![]() deviates from our quantity
deviates from our quantity
![]() (Eq. B1) by the same factor. Noting these
correspondences and keeping our radial streaming approximation,
(Eq. B1) by the same factor. Noting these
correspondences and keeping our radial streaming approximation, ![]() is
defined by
is
defined by
which is nothing else than the force-multiplier if all lines were optically
thin (cf. Eq. 11). On the other hand, from
Eq. (16) we find an intuitive interpretation of
![]() ,
which is
roughly the fraction of the total stellar flux which would be blocked
already in the photosphere if all
lines were optically thick (assuming that each optically thick line
blocks a fraction
,
which is
roughly the fraction of the total stellar flux which would be blocked
already in the photosphere if all
lines were optically thick (assuming that each optically thick line
blocks a fraction
![]() ), divided by
), divided by ![]() .
In so far, the
physical upper limit of
.
In so far, the
physical upper limit of
![]() is of order
is of order ![]() .
(Much earlier,
however, the lines would overlap in the wind, and this effect would
have to be accounted for, e.g. Puls [1987].)
.
(Much earlier,
however, the lines would overlap in the wind, and this effect would
have to be accounted for, e.g. Puls [1987].)
With definition (37) and using a line-distribution function with
exponential cutoff at ![]() (cf. B1) in order to prevent the
number of strong lines from becoming smaller than unity, Gayley showed the
correspondence (his Eq. (56))
(cf. B1) in order to prevent the
number of strong lines from becoming smaller than unity, Gayley showed the
correspondence (his Eq. (56))
in our notation. So far, the ![]() formalism seems to be of no major
conceptual advantage compared to the CAK formalism. The interesting point,
however, is the following: For power-law distributed line-strength
distribution functions with (roughly) constant
formalism seems to be of no major
conceptual advantage compared to the CAK formalism. The interesting point,
however, is the following: For power-law distributed line-strength
distribution functions with (roughly) constant ![]() and conditions valid
for hot winds, one easily finds (cf. Sect. 3.3 and Appendix C) that
and conditions valid
for hot winds, one easily finds (cf. Sect. 3.3 and Appendix C) that
| (39) |
a relation which was invoked by Gayley as a generally valid Ansatz, i.e.,
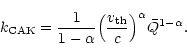 |
(40) |
(Gayley's Eq. (43), with stellar continuum flux ![]() and usual Eddington
and usual Eddington
![]() ). In contrast, the standard formulation (in the same
normalization) implies
). In contrast, the standard formulation (in the same
normalization) implies
with a much more varying value of
![]() .
(Actually, both expressions have
to be slightly modified for the so-called
.
(Actually, both expressions have
to be slightly modified for the so-called ![]() -term accounting for
ionization effects, if present, cf. Abbott [1982] and Kudritzki et
al. [1989]). By comparing both equations, the different philosophy
of
-term accounting for
ionization effects, if present, cf. Abbott [1982] and Kudritzki et
al. [1989]). By comparing both equations, the different philosophy
of ![]() and
and
![]() is evident: the force-multiplier like quantity
is evident: the force-multiplier like quantity
![]() acts on the acceleration ratio
acts on the acceleration ratio ![]() ,
whereas the flux-ratio like
quantity
,
whereas the flux-ratio like
quantity
![]() acts on the stellar flux!
acts on the stellar flux!
If, on the other hand, ![]() differs significantly from
differs significantly from ![]() ,
Eq. (41) has to be modified by an additional factor
,
Eq. (41) has to be modified by an additional factor
![]() ,
and the gain of the
,
and the gain of the ![]() formalism were lost, since then the variation in
formalism were lost, since then the variation in
![]() would be found again in a variation of
would be found again in a variation of ![]() .
In how far this might
be a problem will be discussed in the next section, after we have described
how we calculate line-distribution functions and derive the appropriate
force-multiplier parameters.
.
In how far this might
be a problem will be discussed in the next section, after we have described
how we calculate line-distribution functions and derive the appropriate
force-multiplier parameters.
Copyright The European Southern Observatory (ESO)