Appendix A: Line force and local slope

In this appendix, we will clarify the question under which circumstances the local slope of (generalized) line-strength distribution functions can be equalized to the CAK force multiplier $\alpha$. Following Eq. (24) in Sect. 2.3.2, this is possible under the condition

$$\bigg\vert\frac{\alpha \bar N_{\{0,k_{-}\}}}{N_{+}} \left(\f... ...-}}\right)^{1 - \alpha}\bigg\vert \ll \frac{k_{\rm 1}}{k_{-}},$$ (A1)

Figure A1: Schematic sketch of two different kinds of line-number distributions, case A (left) and B (right). Note the log-log representation necessary to derive the local slope $\alpha -1$, in contrast to the linear representation of Fig. 1 required to calculate the line acceleration. Note also that the displayed minimum line-strength is ${\rm log}\,k_{\rm L}=0$. For an explanation of the various symbols, see also Sect. 2.3.2

which depends strongly on the average cumulative line number $\bar N_{\{0,k_{-}\}}$ (cf. Eq. 25). To proceed further, we have to investigate two cases. Case A, which is the more realistic one (cf. Sect. 4), comprises a situation where the line-number distribution has a monotonic curvature in the log, corresponding to an increase of $\alpha$ for decreasing $k_{\rm L}$. This situation is sketched on the left of Fig. A1: Both the total line number N(0) (as well as $N({\rm log}\,k_{\rm L}=0)$ denoted by N₀ in our plots) and the average number of lines $\bar N_{\{0,k_{-}\}}$ lie well below the extrapolated value $\tilde N$. In this case, it is straightforward to show that the lhs of (A1) obtains its maximum value for the smallest value possible for $\bar N_{\{0,k_{-}\}}$, which is N_-. Using this value, the inequality becomes

$$\vert\,\alpha -1 \vert \ll \left(\frac{k_{\rm 1}}{k_{-}}\right)^{\alpha},$$ (A2)

which under the considered circumstances can be (almost) always fulfilled as long as $\alpha > 0\,$! Thus, for monotonically curved but otherwise unconstrained ${\rm log}N(k_{\rm L})$ distributions (case A), the ensemble line acceleration follows the local (however not necessarily constant) slope of the flux-weighted and cumulative line-strength distribution function, as long as this is larger than -1.

Case B (right panel of Fig. A1) displays the situation of a sharply increasing line number below a certain threshold value k_*. The asymptotic fit value $\tilde N$ is here significantly smaller than the actual value N(0) and the average value $\bar N_{\{0,k_{-}\}}$. In this case, we define N_* as the number of lines where the actual distribution and the fitted one cross each other, at line-strength k_*. To obtain an upper limit for our inequality (A1), we use the maximum possible value for $\bar N_{\{0,k_{-}\}}$,

$${\rm Max}(\bar N_{\{0,k_{-}\}})\,k_{-}= N(0)\,k_{*}\,+\,\int_... ...+}k_{+}^{1 - \alpha}k_{\rm L}^{\alpha - 1}\,{\rm d}k_{\rm L},$$

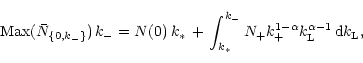
which after some algebra leads to the requirement

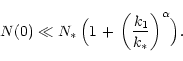$$N(0) \ll N_{*}\, \Bigl(1\,+\,\left(\frac{k_{\rm 1}}{k_{*}}\right)^{\alpha} \Bigr).$$ (A3)

This requirement can be usually fulfilled if $k_{\rm 1}$ is large compared to k_* (i.e., the sharp increase of line number occurs at relatively small line-strength), and, again, if $\alpha$ is positive.

In summary, we have shown that the CAK representation $g_{\rm rad}^{\rm tot} \propto k_{\rm 1}^{\alpha}$ with $\alpha$ corresponding to the local slope of the line-strength distribution function is valid under fairly general circumstances, if the slope is not too steep in the region around $k_{\rm 1}$, i.e., $0 < \alpha \le 1$ locally. Of course, if the distribution function is curved, this leads immediately to depth dependent force-multiplier parameters.

Finally, it is important to realize that our derivation has required some knowledge of the behaviour of optically thin lines, however did not constrain the distribution of optically thick lines in any respect. This, of course, is related to the fact that all optically thick lines behave similarly. Thus, the slope of the distribution for $k_{\rm L}> k_{\rm 1}$ is of no concern as long as we know the actual number of these lines.