

Up: On the automatic folding
Subsections
2 The problem of folding
A typical unreduced rotation curve is shown in Fig. 1 and, in this
figure, the origin of the angular coordinate axis denotes the measured optical
centre,
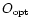 say, of the galaxy; apart from projection corrections
(required because spiral galaxies are
generally not seen edge-on), a successful folding of this rotation curve
requires (a) an accurate estimate of the cosmological redshift,
say, of the galaxy; apart from projection corrections
(required because spiral galaxies are
generally not seen edge-on), a successful folding of this rotation curve
requires (a) an accurate estimate of the cosmological redshift,
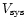 say, that must be subtracted from the velocity measurements along the
whole curve; (b) an accurate estimate of the dynamical centre,
say, that must be subtracted from the velocity measurements along the
whole curve; (b) an accurate estimate of the dynamical centre,
 say, of the rotation curve.
say, of the rotation curve.
 |
Figure 1:
Typical unfolded rotation curve |
The MFB data-base for the unreduced curves provides approximations for
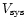 and
and
 (this latter being identified with
(this latter being identified with
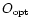 )
which are
sufficiently good for the peculiar velocity studies which motivated MFB but
not good enough for the dynamical studies which motivated PS.
So, the problem resides entirely in the accuracy with which
)
which are
sufficiently good for the peculiar velocity studies which motivated MFB but
not good enough for the dynamical studies which motivated PS.
So, the problem resides entirely in the accuracy with which
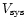 and
and
 can be determined, and the major obstacle to obtaining this accuracy
is simply the noisiness of rotation curve data - if the galaxies from which the
data was drawn were perfectly rotationally symmetric, and if the measurements
were exact, then it would be a trivial task to find the centre of asymmetry of
any rotation curve.
can be determined, and the major obstacle to obtaining this accuracy
is simply the noisiness of rotation curve data - if the galaxies from which the
data was drawn were perfectly rotationally symmetric, and if the measurements
were exact, then it would be a trivial task to find the centre of asymmetry of
any rotation curve.
2.1 Assessment of noise in MFB 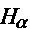 velocity data
velocity data
As a means of determining the level of noise in each velocity measurement, MFB
provided a cross-correlation coefficient,
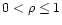 ,
derived by
comparing the H
,
derived by
comparing the H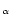 line profile with an artificial template line profile
(see MFB for details).
In their analysis, PS found that selecting those velocities for
which
line profile with an artificial template line profile
(see MFB for details).
In their analysis, PS found that selecting those velocities for
which
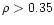 gave a mean rms of less than about 10 km s-1, whilst for
gave a mean rms of less than about 10 km s-1, whilst for
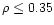 an rms of up to 20 km s-1 was to be expected.
For this reason, they restricted their data to values for which
an rms of up to 20 km s-1 was to be expected.
For this reason, they restricted their data to values for which
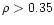 .
.
In our development, we have found that
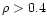 is necessary for the
accurate operation of the auto-folder being developed.
is necessary for the
accurate operation of the auto-folder being developed.


Up: On the automatic folding
Copyright The European Southern Observatory (ESO)
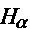 velocity data
velocity data
![]() is necessary for the
accurate operation of the auto-folder being developed.
is necessary for the
accurate operation of the auto-folder being developed.