1 Introduction

Rotation curves are the primary source of information about spiral galaxy dynamics and, as such, they are essential tools for any programme which seeks to determine relationships between dynamics and mass distributions in spiral galaxies - whether this is for dark matter studies, or for testing gravitational theories. However, before they can be used in any dynamical context, they must be accurately folded. Prior to the PS contribution of 900 accurately folded optical rotation curves, there was no large data base available and, so far as we are aware, even though a large amount of unfolded data is available, no other large data base of folded rotation curves has subsequently been made available. The reason for this absence is most probably that rotation curve folding has hitherto been a labour-intensive "by eye'' process - fine for small volumes of data, but extremely time consuming for large volumes of data. For this reason, we undertook to attempt the development of an automatic folding process. In the event, it has turned out that a successful development has only been possible because of the availability of the PS data-base of 900 folded rotation curves which has acted as an essential template against which the performance of the auto-folder described here was judged in the various stages of its development. In addition to this, the development has required the recognition, and use, of certain correlations (previously unsuspected, so far as we are aware) which point directly to underlying physical processes, the study of which may lead to a deeper understanding of spiral galaxies and their evolution.

The PS sample of folded optical rotation curves was analysed in Roscoe 1999A, and gave rise to the following primary result: defining R to be the radial displacement from the kinematic centre and V to be the rotational velocity at radial displacement R, then, to a very high statistical precision, rotation curves conform to the law

 

$${ V \over V_0 } \left( { R \over R_0 } \right)^\alpha$$ = (1)

$$\log V_0 \approx -0.584 - 0.133 \,M - 0.000243\, S,$$

$$\log R_0 \approx -3.291 - 0.208 \,M - 0.00292\, S,$$

where M denotes absolute magnitude, S denotes surface brightness and 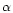$\alpha$ is a parameter, constant for any given galaxy, but which which varies between galaxies. The high statistical precision which accompanied this result implied, in its turn, that the PS folding process was very reliable and that their sample of folded rotation curves could be considered as a "model solution'' against which the success, or otherwise, of any automatic folding algorithm could be properly judged. Consequently, in all that follows, the developing auto-folder is continually tested by using it to fold the raw MFB data which formed the core of the PS sample, and comparing the resulting solution with the PS solution over the same sample.

In Sect. 2 we describe the general problem of folding rotation curves whilst, in Sect. 3, we describe precisely what quality of the PS model solution is used to judge the automatic folding algorithm under development and in Sect. 4 we briefly discuss a class of methods which were considered, but proved to be insufficiently robust.

In the remaining sections we provide a sequential description of a robust auto-folder development paying particular attention to the difficulties which arose, and to the manner of their resolution.