

Up: On the automatic folding
Subsections
3 The adopted measure of folding quality
The very noisy nature of rotation curve data means that any solution to
the folding of any given rotation curve is likely to contain a large element of
uncertainty; it follows that, given two reasonable folding techniques, there
are likely to be many rotation curves which are best folded by one particular
technique, and vice-versa for other rotation curves whilst, at the same
time, any objective judgement about which are the best individual solutions
is likely to be extremely difficult (if not impossible) at best.
It follows that any judgement about the relative merits of any
two folding methods must be made by some global statistical method applied
to the folded solution of a large number of rotation curves.
The method used for the present development is described in the following.
As we have indicated, the basic result (shorn of the fine details) of
Roscoe 1999A was that optical rotation curve data is described, to a high
statistical precision, by the power-law structure
 where
where
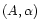 are constants which differ from galaxy to galaxy.
Essentially, but with the "hole-cutting'' data-reduction process described
in Roscoe 1999A,
are constants which differ from galaxy to galaxy.
Essentially, but with the "hole-cutting'' data-reduction process described
in Roscoe 1999A, 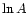 and
and 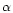 for each rotation curve were
determined by linear regression of
for each rotation curve were
determined by linear regression of 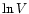 data on
data on  data.
Thus, for the PS sample of 900 good quality rotation curves we obtain
900 pairs
data.
Thus, for the PS sample of 900 good quality rotation curves we obtain
900 pairs
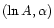 .
.
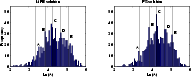 |
Figure 2:
Comparison of MFB and PS solutions.
The vertical lines in both diagrams indicate the positions of the A, B, C, D
and E peaks in the PS solution |
Figure 2 (left) shows the 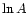 distribution for the MFB solution
(that is, when the rotation curves are folded using MFB's optical centre and their estimate
of
distribution for the MFB solution
(that is, when the rotation curves are folded using MFB's optical centre and their estimate
of
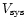 ), whilst Fig. 2 (right) shows the corresponding distribution
for the PS solution.
A comparison shows that the peaks labelled B, C and D in the MFB solution are reproduced -
enhanced and with much reduced noise - in the PS solution.
Since the MFB solutions were determined directly from observational estimates of optical
centres and systematic redshifts whilst the PS solutions were determined using a "by-eye''
folding process without any reference to an underlying power-law structure
(and hence without reference to any
), whilst Fig. 2 (right) shows the corresponding distribution
for the PS solution.
A comparison shows that the peaks labelled B, C and D in the MFB solution are reproduced -
enhanced and with much reduced noise - in the PS solution.
Since the MFB solutions were determined directly from observational estimates of optical
centres and systematic redshifts whilst the PS solutions were determined using a "by-eye''
folding process without any reference to an underlying power-law structure
(and hence without reference to any 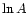 distribution),
then the foregoing comparison strongly suggests that the B, C, D peak structure reflects
objective physical qualities in the underlying distribution of rotation curves.
This conclusion was reached independently (with the addition of the A and E peaks), supported
by very strong statistics, in Roscoe 1999B.
distribution),
then the foregoing comparison strongly suggests that the B, C, D peak structure reflects
objective physical qualities in the underlying distribution of rotation curves.
This conclusion was reached independently (with the addition of the A and E peaks), supported
by very strong statistics, in Roscoe 1999B.
For these reasons, the 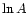 distribution is adopted here as a suitable statistical
representation of a folding solution over a large number of rotation curves.
distribution is adopted here as a suitable statistical
representation of a folding solution over a large number of rotation curves.


Up: On the automatic folding
Copyright The European Southern Observatory (ESO)


![]() distribution is adopted here as a suitable statistical
representation of a folding solution over a large number of rotation curves.
distribution is adopted here as a suitable statistical
representation of a folding solution over a large number of rotation curves.