12 The Mk IV auto-folder

The considerations of the previous section have led us to conclude that the Mk IV auto-folder is to be defined as a composite of the Mk II auto-folder used in the ranges $2.2 < \ln A \leq 4.2$ and $4.5 < \ln A \leq 4.8$, and the Mk III auto-folder in $4.2 < \ln A \leq 4.5$and $4.8 < \ln A \leq 6$. Bearing in mind that these ranges were defined via an analysis based on the sole use of the Mk II auto-folder, the implication is that the folding process begins by using the Mk II auto-folder for all rotation curves and, when the resulting $\ln A$ lies in one of the appropriate ranges, the solution is repeated using the Mk III auto-folder.

After some marginal fine-tuning of the given $\ln A$ ranges, a workable definition of the Mk IV auto-folder can be given as follows:

• Use the Mk II auto-folder over the whole sample;
• Calculate the resulting $\ln A$ for each rotation curve in the manner described in Sect. 3 and Appendix B;
• Whenever $4.22 < \ln A \leq 4.55$ or $4.8 < \ln A \leq 6$, then continue with the Mk III strategy; see Sect. 9. Occasionally, this secondary process fails to re-fold the rotation curve, in which case the original Mk II solution is used.

12.1 Results and implications

The results of applying this to the PS sample are shown in Fig. 6.

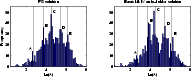Figure 6: Left: PS solution; Right: Mk IV Auto-folder applied to PS sample. The vertical lines indicate the positions of the A, B, C, D and E peaks in the PS solution

It is at once apparent that the Mk IV auto-folder provides a huge improvement over the Mk II and Mk III auto-folders and, on the basis of its ability to produce a high fidelity copy of the peak-structure of the PS solution (Fig. 6 left), the Mk IV auto-folder is accepted as the best achievable with present resources.

The Mk IV auto-folder strategy was based on the working hypothesis (cf. Sect. 11.1), that significant changes in $(R_{{\rm min}},R_{{\rm opt}})$ correlations through the hole-cutting process are indicative of rotation curves with intrinsically noisy transition regions. This strategy has been manifestly so successful that its success must be considered as very strong circumstantial evidence supporting the view that the working hypothesis on which it is based is correct. Thus, cross-referencing Table 1 with Fig. 6 (right), we see that strong circumstantial evidence exists to suggest that the rotation curves associated with the peaks C and E have intrinsically noisier transition regions on their interiors than do those associated with the peaks B and D.

Finally, we note from Table 1 that the transition region behaviours of the two "quiet transition region'' peaks, B and D, are mutually distinct: specifically, for the B peak, the coefficient of determination changes from 20.7% to 26.3% through hole-cutting - and each of these values signifies a very strong $(R_{{\rm min}},R_{{\rm opt}})$ correlation; by contrast, for the D peak, the coefficient of determination changes from 1.9% to 8.4% - the first value signifies a very weak $(R_{{\rm min}},R_{{\rm opt}})$ correlation whilst the second signifies a moderately weak $(R_{{\rm min}},R_{{\rm opt}})$ correlation.

As we have already noted, the sample sizes are sufficiently great that we can discount random statistical fluctuations as the source of these differences between the B and D peak rotation curves, and so the question arises of why strong $(R_{{\rm min}},R_{{\rm opt}})$ correlations are present for B peak rotation curves, but are more-or-less absent for D peak rotation curves? Since the existence of strong correlations implies the existence of some coherent physical process, the question becomes, why are the correlating effects of this physical process not present for the D peak rotation curves?

These considerations all point to the need of further research.

12.2 Some examples of folded rotation curves

Figures 7 and 8 give examples of ten rotation curves folded using the auto-folder, and the corresponding PS solution for these rotation curves - the examples were chosen as representative of the whole set, and not for any particular qualities they display.

Figure 7: Five folded rotation curves: Left auto-folder soluton; Right PS solution

Figure 8: Five folded rotation curves: Left auto-folder soluton; Right PS solution

Figure 9: Folding of simulated low-density sampling rotation curves

Figure 10: Folding of simulated medium-density sampling rotation curves

Figure 11: Folding of simulated high-density sampling rotation curves

Whilst there are differences in detail for the two folds of any given rotation curve, there is no obvious sense in which either of the solutions is the superior one.