

Up: On the automatic folding
Subsections
13 Folding of simulated rotation curves
So far, the efficacy of the developed auto-folder has been judged by means of a comparison of
the PS folding solution and the auto-folder's
solution defined on the same sample; the assumption is, of course, that the PS solution
over the sample can be considered "correct'' in an overall statistical sense.
However, in the absence of objective certainties, it is useful to see how the auto-folder
deals with the folding of simulated rotation curves for which the folded solution is
known a priori.
The following describes the results of applying the auto-folder to three sets of five
simulated rotation curves per set, where each set is chosen to represent a particular
sampling regime - low-density sampling, medium-density sampling and high-density sampling.
The considerations of Roscoe (1999A) show that, to an extremely high level of statistical
precision, optical rotation curves conform to a power-law,
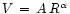 for
for
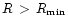 where
where
 defines the exterior limit of the dynamical effects of
the bulge on the disc.
defines the exterior limit of the dynamical effects of
the bulge on the disc.
Given this, and in order to preserve maximum authenticity otherwise, we used the existing
PS sample as the basis for generating simulated unfolded rotation curves as follows:
- fold the PS sample using the auto-folder and record the set of parameters,
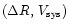 ,
which define each folding solution.
Here,
,
which define each folding solution.
Here, 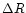 is the offset between MFB's estimated dynamical centre and the
auto-folder's estimated dynamical centre, whilst
is the offset between MFB's estimated dynamical centre and the
auto-folder's estimated dynamical centre, whilst
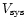 is the auto-folder's
estimated systematic velocity for the galaxy concerned;
is the auto-folder's
estimated systematic velocity for the galaxy concerned;
-
record the sampling radii,
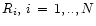 on each rotation curve, and
note which is on the approaching arm and which is on the receding arm;
on each rotation curve, and
note which is on the approaching arm and which is on the receding arm;
-
at each radial position,
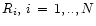 ,
on any give rotation curve, record the
value of the cross-correlation coefficient,
,
on any give rotation curve, record the
value of the cross-correlation coefficient, 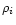 ,
used by MFB to indicate the
quality of velocity measurement at Ri - see Sect. 2.1;
,
used by MFB to indicate the
quality of velocity measurement at Ri - see Sect. 2.1;
-
calculate A,
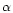 and
and
 for each rotation curve;
for each rotation curve;
-
for
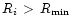 ,
form
,
form
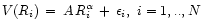 where
where
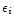 is a normal random variable defined so that
95% of its values lie within the interval [-a,+a] km s-1 when
is a normal random variable defined so that
95% of its values lie within the interval [-a,+a] km s-1 when
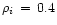 ,
and within the interval
[-a/6,+a/6] km s-1 when
,
and within the interval
[-a/6,+a/6] km s-1 when
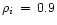 .
Here, a is a positive parameter with a typical value of 20 km s-1;
.
Here, a is a positive parameter with a typical value of 20 km s-1;
-
in the absence of any quantitative knowledge in the region
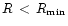 ,
we
simply form
,
we
simply form
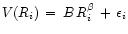 in this region,
where B is chosen to ensure continuity of velocity across
in this region,
where B is chosen to ensure continuity of velocity across
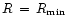 ,
and
,
and 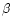 is a normal random variable chosen so that 95% of its values
lie within the interval [0,1];
is a normal random variable chosen so that 95% of its values
lie within the interval [0,1];
-
unfold the rotation curve by assigning to each velocity,
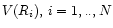 ,
a
positive or negative signature according to whether the sampling radius, Ri, is on
an approaching or receding arm;
,
a
positive or negative signature according to whether the sampling radius, Ri, is on
an approaching or receding arm;
-
make a random selection of
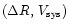 from the previously computed list, and
transform the unfolded rotation curve according to
from the previously computed list, and
transform the unfolded rotation curve according to
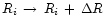 and
and
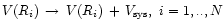 ;
;
-
apply the auto-folder to the folding of these simulated rotation curves.
When the velocity noise parameter,
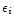 ,
is set to zero, then the
auto-folder folds all of the simulated rotation curves (864 of them) exactly,
to within rounding errors.
This demonstrates that the general logic of the underlying algorithm is working
correctly.
,
is set to zero, then the
auto-folder folds all of the simulated rotation curves (864 of them) exactly,
to within rounding errors.
This demonstrates that the general logic of the underlying algorithm is working
correctly.
Typically realistic simulated rotation curves resulted when
the velocity noise parameter,
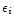 ,
was defined by setting a = 20 km s-1 in the
foregoing prescription.
The results of applying the auto-folder to the folding of a sample of these noisy curves
are shown in Figs. 9, 10 and 11
respectively.
In all cases, it is seen that the auto-folder solution has the appearance of being
reasonable in the sense that it is not obvious that the exact solution is necessarily
better.
However, a detailed comparison of the exact solutions with the auto-folder's solutions
shows that, in general, the auto-folder's solutions improve as the sampling rate
increases; this is a reasonable and expected result.
,
was defined by setting a = 20 km s-1 in the
foregoing prescription.
The results of applying the auto-folder to the folding of a sample of these noisy curves
are shown in Figs. 9, 10 and 11
respectively.
In all cases, it is seen that the auto-folder solution has the appearance of being
reasonable in the sense that it is not obvious that the exact solution is necessarily
better.
However, a detailed comparison of the exact solutions with the auto-folder's solutions
shows that, in general, the auto-folder's solutions improve as the sampling rate
increases; this is a reasonable and expected result.


Up: On the automatic folding
Copyright The European Southern Observatory (ESO)
![]() ,
was defined by setting a = 20 km s-1 in the
foregoing prescription.
The results of applying the auto-folder to the folding of a sample of these noisy curves
are shown in Figs. 9, 10 and 11
respectively.
In all cases, it is seen that the auto-folder solution has the appearance of being
reasonable in the sense that it is not obvious that the exact solution is necessarily
better.
However, a detailed comparison of the exact solutions with the auto-folder's solutions
shows that, in general, the auto-folder's solutions improve as the sampling rate
increases; this is a reasonable and expected result.
,
was defined by setting a = 20 km s-1 in the
foregoing prescription.
The results of applying the auto-folder to the folding of a sample of these noisy curves
are shown in Figs. 9, 10 and 11
respectively.
In all cases, it is seen that the auto-folder solution has the appearance of being
reasonable in the sense that it is not obvious that the exact solution is necessarily
better.
However, a detailed comparison of the exact solutions with the auto-folder's solutions
shows that, in general, the auto-folder's solutions improve as the sampling rate
increases; this is a reasonable and expected result.