

Up: On the automatic folding
Subsections
11 A detailed investigation of the effects of hole-cutting
The considerations of the previous section indicate the possibility
that a selective application of the Mk II and Mk III auto-folders might be
beneficial.
But the only possible objective justification for using the active
hole-cutting process of the Mk III auto-folder selectively is that the
transition regions of the selected rotation curves are intrinsically
noisier than the transition regions of the non-selected rotation curves.
This raises the question of how we can
determine which rotation curves have intrinsically noisy transition regions.
11.1 A working hypothesis
A consideration of the relative strengths of the B and C peaks in each of the
diagrams of Fig. 5 provides prima facie evidence
for the idea that C-peak rotation curves have intrinsically noisy transition
regions (since hole-cutting has increased the strength of the C peak), whilst
B-peak rotation curves have relatively quiet transition regions (since hole-cutting
has decreased the strength of the B peak).
Since rotation curves with intrinsically noisy transition regions will necessarily
be subject to more inaccurate folding than other rotation curves then, by
the observations of Appendix D, it might be expected
that C-peak rotation curves will be associated with correspondingly
greater changes in
 correlations through hole-cutting
than B-peak rotation curves.
correlations through hole-cutting
than B-peak rotation curves.
Generalizing, this leads to the working hypothesis that an analysis
of changes in
 correlations through the hole-cutting
process as a function of
correlations through the hole-cutting
process as a function of 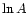 might
reveal significant non-uniformities indicating corresponding non-uniformities in
the distribution of rotation curves with intrinsically noisy transition regions.
This eventuality would then provide the required objective rationale of when to
employ hole-cutting as an active component of the folding process, and when not to.
The following subsections describe this analysis.
might
reveal significant non-uniformities indicating corresponding non-uniformities in
the distribution of rotation curves with intrinsically noisy transition regions.
This eventuality would then provide the required objective rationale of when to
employ hole-cutting as an active component of the folding process, and when not to.
The following subsections describe this analysis.
We require a detailed assessment of the effects of the hole-cutting
strategy on
 correlations as a function of
correlations as a function of 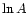 .
Since the potential objective is to determine for what values
of
.
Since the potential objective is to determine for what values
of 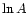 the Mk III auto-folder should be used and since, in practice, these values of
the Mk III auto-folder should be used and since, in practice, these values of
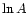 will be obtained via the prior use of the Mk II auto-folder (cf. Sect. 9),
it follows that the
will be obtained via the prior use of the Mk II auto-folder (cf. Sect. 9),
it follows that the
 values used in the proposed analysis should likewise
be drawn from Mk II auto-folder solutions.
values used in the proposed analysis should likewise
be drawn from Mk II auto-folder solutions.
Comparing the Mk II and Mk III auto-folder solutions of Fig. 5,
we were able to identify an approximate partition of the range
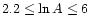 in
which to study the effects of the hole-cutting strategy and, with a little experimentation,
were able to refine this into the four cases,
in
which to study the effects of the hole-cutting strategy and, with a little experimentation,
were able to refine this into the four cases,
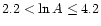 ,
,
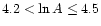 ,
,
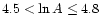 and
and
 .
.
It is to be emphasized that, although the foregoing ranges were identified by numerical
experimentation, the changes in the behaviour of the
 correlations
between these ranges are so strong, and the sample sizes so large, that the ordinary
processes of random statistical fluctuation as a source of the variations can be ruled
out with virtual certainty; consequently, considerable reliance can be placed on qualitative
deductions made from the results summarized in Table 1 which lists the pre-hole
cutting and the post-hole cutting values of the indices of determination, R2, for each
of the four
correlations
between these ranges are so strong, and the sample sizes so large, that the ordinary
processes of random statistical fluctuation as a source of the variations can be ruled
out with virtual certainty; consequently, considerable reliance can be placed on qualitative
deductions made from the results summarized in Table 1 which lists the pre-hole
cutting and the post-hole cutting values of the indices of determination, R2, for each
of the four 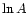 ranges:
ranges:
Table 1:
Effects of hole-cutting on coefficient of determination
| |
R2 before |
R2 after |
|
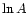 range
range |
hole-cutting |
hole-cutting |
N |
|
(2.2, 4.2] |
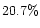 |
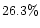 |
348 |
|
(4.2, 4.5] |
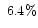 |
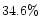 |
150 |
|
(4.5, 4.8] |
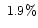 |
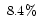 |
141 |
|
(4.8, 6.0] |
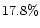 |
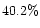 |
224 |
It is clear that there are two distinct modes of behaviour for changes
in the
 correlation through the hole-cutting process:
there are very strong changes in
correlation through the hole-cutting process:
there are very strong changes in 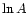 ranges
(4.2, 4.5] and
(4.8, 6.0],
and relatively weak changes in
ranges
(4.2, 4.5] and
(4.8, 6.0],
and relatively weak changes in 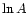 ranges
(2.2, 4.2] and
(4.5, 4.8]Recalling our working hypothesis (cf. Sect. 11.1)
that significant change in the
ranges
(2.2, 4.2] and
(4.5, 4.8]Recalling our working hypothesis (cf. Sect. 11.1)
that significant change in the
 correlation is potentially
indicative of rotation curves with intrinsically noisy transition regions,
then Table 1 provides an objective rationale for
employing the Mk III auto-folder on the sub-intervals
correlation is potentially
indicative of rotation curves with intrinsically noisy transition regions,
then Table 1 provides an objective rationale for
employing the Mk III auto-folder on the sub-intervals
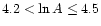 and
and
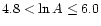 ,
but not on the remaining intervals.
,
but not on the remaining intervals.


Up: On the automatic folding
Copyright The European Southern Observatory (ESO)
![]() correlations through hole-cutting
than B-peak rotation curves.
correlations through hole-cutting
than B-peak rotation curves.
![]() correlations through the hole-cutting
process as a function of
correlations through the hole-cutting
process as a function of ![]() might
reveal significant non-uniformities indicating corresponding non-uniformities in
the distribution of rotation curves with intrinsically noisy transition regions.
This eventuality would then provide the required objective rationale of when to
employ hole-cutting as an active component of the folding process, and when not to.
The following subsections describe this analysis.
might
reveal significant non-uniformities indicating corresponding non-uniformities in
the distribution of rotation curves with intrinsically noisy transition regions.
This eventuality would then provide the required objective rationale of when to
employ hole-cutting as an active component of the folding process, and when not to.
The following subsections describe this analysis.
![]() in
which to study the effects of the hole-cutting strategy and, with a little experimentation,
were able to refine this into the four cases,
in
which to study the effects of the hole-cutting strategy and, with a little experimentation,
were able to refine this into the four cases,
![]() ,
,
![]() ,
,
![]() and
and
![]() .
.
![]() correlations
between these ranges are so strong, and the sample sizes so large, that the ordinary
processes of random statistical fluctuation as a source of the variations can be ruled
out with virtual certainty; consequently, considerable reliance can be placed on qualitative
deductions made from the results summarized in Table 1 which lists the pre-hole
cutting and the post-hole cutting values of the indices of determination, R2, for each
of the four
correlations
between these ranges are so strong, and the sample sizes so large, that the ordinary
processes of random statistical fluctuation as a source of the variations can be ruled
out with virtual certainty; consequently, considerable reliance can be placed on qualitative
deductions made from the results summarized in Table 1 which lists the pre-hole
cutting and the post-hole cutting values of the indices of determination, R2, for each
of the four ![]() ranges:
ranges: