 |
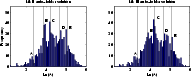
Figure 5: Comparison of Mk II and Mk III auto-folder solutions. The vertical lines indicate the positions of the A, B, C, D and E peaks in the PS solution |
 |
Figure 5: Comparison of Mk II and Mk III auto-folder solutions. The vertical lines indicate the positions of the A, B, C, D and E peaks in the PS solution |
Copyright The European Southern Observatory (ESO)