

Up: On the automatic folding
Subsections
6 The Mk I auto-folder
The basic folding technique is developed from the idea that any function,
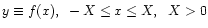 can be decomposed into
two parts, one of which is asymmetric on the region about x=0 and one of which
is symmetric on the region about x=0.
can be decomposed into
two parts, one of which is asymmetric on the region about x=0 and one of which
is symmetric on the region about x=0.
In the present case, and for ideal data, once
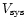 has been found and
accounted for by subtraction from the measured rotation velocities, then the
resulting processed rotation curve should be perfectly
asymmetric about
has been found and
accounted for by subtraction from the measured rotation velocities, then the
resulting processed rotation curve should be perfectly
asymmetric about
 ,
its dynamical centre.
However, suppose we have
,
its dynamical centre.
However, suppose we have
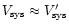 and
and
 then, after subtracting
then, after subtracting
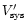 the curve will
be only approximately asymmetric about the assumed dynamical origin,
the curve will
be only approximately asymmetric about the assumed dynamical origin,
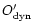 - and can therefore be considered composed of an exact asymmetric
part together with an exact symmetric part.
The basic folding technique therefore consists in minimizing the symmetric
component with respect to variations in the estimates of
- and can therefore be considered composed of an exact asymmetric
part together with an exact symmetric part.
The basic folding technique therefore consists in minimizing the symmetric
component with respect to variations in the estimates of
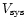 and
and
 .
.
The symmetric component,
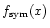 ,
of any function
,
of any function
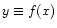 defined
on the interval
defined
on the interval
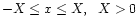 can be calculated using the
finite cosine transform:
can be calculated using the
finite cosine transform:
If the function represents a rotation curve then, in practice,
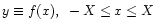 is replaced by a numerical function defined
at N+1 points on the discretized interval
is replaced by a numerical function defined
at N+1 points on the discretized interval
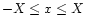 .
Suppose that this numerical function is given as
(x0,f0),...,(xN,fN).
In the ideal case, for which x0=-X and xN=X, then the Fourier component,
A(m), can be approximated by a direct numerical integration of (2).
However, the more usual case will be that the numerical function is defined over
a non-symmetric interval (for example,
.
Suppose that this numerical function is given as
(x0,f0),...,(xN,fN).
In the ideal case, for which x0=-X and xN=X, then the Fourier component,
A(m), can be approximated by a direct numerical integration of (2).
However, the more usual case will be that the numerical function is defined over
a non-symmetric interval (for example,
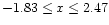 ).
In this case, the requirements of the cosine transform makes it necessary to
discard and/or interpolate points of the numerical function so that it becomes
defined over the largest symmetric interval that can be fitted into the original
non-symmetric interval; in the case of the example, this would be
).
In this case, the requirements of the cosine transform makes it necessary to
discard and/or interpolate points of the numerical function so that it becomes
defined over the largest symmetric interval that can be fitted into the original
non-symmetric interval; in the case of the example, this would be
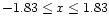 .
.
6.2 How many Fourier modes should be computed?
In very simple situations, for which the numerical function is defined at
equal intervals, 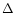 say, in the independent variable, there is no point in
calculating Fourier modes which have a wave-length less than
say, in the independent variable, there is no point in
calculating Fourier modes which have a wave-length less than 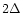 .
This leads to the standard rule that the computation of N Fourier modes
requires a minimum of 2N + 1 data points, when these are equally spaced.
Conversely, a given number of points then informs how many Fourier modes it
is worthwhile including.
.
This leads to the standard rule that the computation of N Fourier modes
requires a minimum of 2N + 1 data points, when these are equally spaced.
Conversely, a given number of points then informs how many Fourier modes it
is worthwhile including.
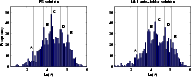 |
Figure 3:
PS solution compared with the Mk I auto-folder solution.
The vertical lines indicate the positions of the A, B, C, D and E peaks in
the PS solution |
However, rotation curve data is very frequently defined over non-equally
spaced intervals and, in this case, the basic rule has to be replaced
by the rule that there is no point in calculating Fourier modes with a
wave-length less that
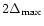 ,
where
,
where
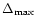 is the
largest interval separating adjacent points on the rotation curve.
is the
largest interval separating adjacent points on the rotation curve.
The foregoing describes how to compute the symmetric Fourier modes for given
estimates of
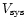 and
and
 .
Suppose M of these are computed, then we form the functional
.
Suppose M of these are computed, then we form the functional
and minimize this with respect to variations in the estimates of
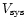 and
and
 .
The very noisy nature of rotation curve data requires that a very robust
minimization procedure, using no derivatives, should be employed.
A routine based on the Simplex algorithm (Nelder & Mead 1965) was found to be
very effective in the present case.
When applied to the PS sample, this Mk I auto-folder gives the
.
The very noisy nature of rotation curve data requires that a very robust
minimization procedure, using no derivatives, should be employed.
A routine based on the Simplex algorithm (Nelder & Mead 1965) was found to be
very effective in the present case.
When applied to the PS sample, this Mk I auto-folder gives the 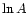 distribution shown in Fig. 3, right.
We immediately see that peaks B, C and D of the PS solution (reproduced in
Fig. 3 left) are excellently reproduced by the Mk I auto-folder;
however, peak E is lost in noise.
distribution shown in Fig. 3, right.
We immediately see that peaks B, C and D of the PS solution (reproduced in
Fig. 3 left) are excellently reproduced by the Mk I auto-folder;
however, peak E is lost in noise.
It is worth emphasizing that the reproduction, in Fig. 3 right, of the
major part of the peak structure of the PS solution confirms that this structure
is not an artifact of the PS procedure but is, at the very least,
inherent to the sample.


Up: On the automatic folding
Copyright The European Southern Observatory (ESO)
![]() has been found and
accounted for by subtraction from the measured rotation velocities, then the
resulting processed rotation curve should be perfectly
asymmetric about
has been found and
accounted for by subtraction from the measured rotation velocities, then the
resulting processed rotation curve should be perfectly
asymmetric about
![]() ,
its dynamical centre.
However, suppose we have
,
its dynamical centre.
However, suppose we have
![]() and
and
![]() then, after subtracting
then, after subtracting
![]() the curve will
be only approximately asymmetric about the assumed dynamical origin,
the curve will
be only approximately asymmetric about the assumed dynamical origin,
![]() - and can therefore be considered composed of an exact asymmetric
part together with an exact symmetric part.
The basic folding technique therefore consists in minimizing the symmetric
component with respect to variations in the estimates of
- and can therefore be considered composed of an exact asymmetric
part together with an exact symmetric part.
The basic folding technique therefore consists in minimizing the symmetric
component with respect to variations in the estimates of
![]() and
and
![]() .
.

![]() ,
where
,
where
![]() is the
largest interval separating adjacent points on the rotation curve.
is the
largest interval separating adjacent points on the rotation curve.
![\begin{displaymath}F(M) = \sum^M_{m=0} \left[ A(m) \right]^2
\end{displaymath}](/articles/aas/full/1999/20/ds8928/img48.gif)