4 Observational inputs for the IRFM

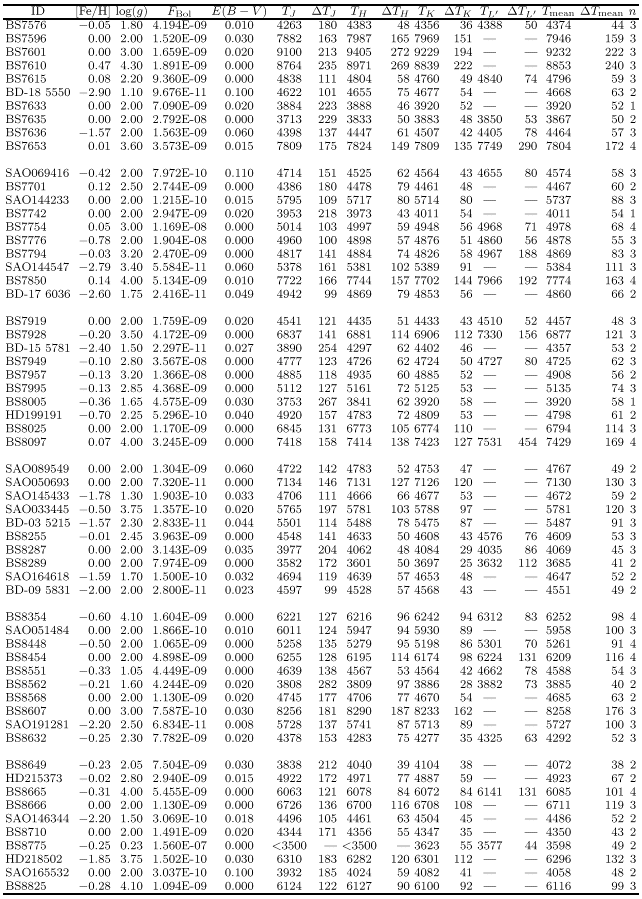
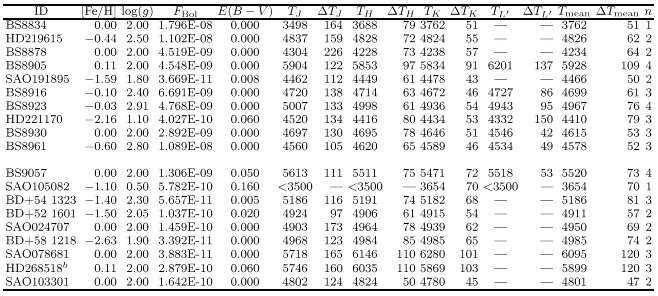
In the following paragraphs the different observational inputs which enter the application of the IRFM are commented on.

4.1 IR monochromatic fluxes

The determination of monochromatic fluxes at wavelengths of the IR continuum requires two observational inputs: Firstly, the measurement of IR photometry for the problem stars with respect to a standard, and secondly the absolute flux calibration of the standard star. Then, entering the IR magnitudes measured in Eq. (2), we obtain monochromatic fluxes at $\lambda_{J}$, $\lambda_{H}$, $\lambda_{K}$ and $\lambda_{L'}$ for each star in the sample.

In Paper II, a semi-empirical method was devised to determine the absolute calibration of the flux of Vega in the near-IR (from J to L'). This absolute calibration places temperatures derived applying the IRFM with Kurucz's models on the same scale as mean direct temperatures derived from angular diameter measurements. It is worth noting the good agreement (within 1%) with the semi-empirical calibration for Vega provided by Walker & Cohen (1992), the theoretical one by Dreiling & Bell (1980) and the "self-consistent'' calibration by Blackwell et al. (1990).

The errors in the absolute IR flux calibration have different effects on the temperatures derived by mean of the IRFM, depending on the photometric band. The errors in the absolute IR flux calibration were estimated at 3% in the J band, 4% in H and K bands and 5% in L' band (Paper II). Over 4000 K, the net effect of this systematic uncertainty is a drift of the temperature scale. If it happens that the above errors correlate in the three (four) bands, the maximum possible variation of the temperature scale would amounts to from 1.2% at 8000 K to 1.7% at 4000 K (1.3-1.7%) over 4000 K. However, if as it is more likely, the errors in the three (four) bands are uncorrelated, the net effect of the uncertainty of the absolute calibration would be an approximately constant shift in the zero point over the whole temperature range amounting to at most 0.9%. Although the indeterminacy of the zero point of the scale is common to all kind of methods used to derive effective temperatures, the method adopted in Paper II to fix the absolute calibration of the flux in the near IR was designed in order to minimising this error.

The programme of broad-band photometry in the near-IR is described in Paper IV. J, H, K (and L') magnitudes were measured for 70% of the stars in the sample, with a mean accuracy of the order of 0.01-0.02 mag for J, H, K and 0.04 mag for L'. For the remainder of the stars, the photometry was obtained from the literature and transformed to the system of the TCS in order to compute near-IR monochromatic fluxes.
The isolated effect of the photometric errors on the $T_{\rm eff}$ determination can be inferred from Tables 1-4, taking Eq. (3) into account.

  

Figure 3: Top: Bolometric correction to $K_{\rm TCS}$ versus $(V-K)_{\rm TCS}$. Solid circles correspond to dwarf stars and open circles to giant stars. Circles: [Fe/H] = 0.0; squares: [Fe/H] = -1.5; triangles: [Fe/H] = -3.0. Bottom: Difference between the bolometric correction to $K_{\rm TCS}$ of dwarf and giant stars

4.2 Bolometric fluxes

For the range of spectral types studied in the present work, nearly all the flux arriving at the earth atmosphere passes through the atmospheric windows. When comparing $F_{\rm Bol}$ derived directly from calibrated spectra to $F_{\rm Bol}$ obtained by integrating UBVRI photometry, Petford et al. (1988) report an accuracy of the order of 2%. Therefore, the bolometric flux might be obtained for each star in the sample from broad-band photometry. However, photometric calibrations of the type provided by Blackwell & Petford (1991) and Blackwell & Lynas-Gray (1998) represent a more practical and accurate approach. We have obtained calibrations of this kind by fitting the bolometric fluxes of 184 stars of the sample, well distributed in metallicity, as a function of K, (V-K) and [Fe/H]. Bolometric fluxes ($F_{\rm Bol}$) have been obtained by integrating UBVRIJHK photometry. The percentage of $F_{\rm Bol}$ measured in U--K bands ranges from 80% to 90% for the giant stars contained in our sample. The energy outside that wavelength range (i.e. UV and far IR flux) has been estimated with the help of models as described thoroughly in Paper III. The low dispersion of the fits grants the overall level of accuracy expected for the final temperatures derived in this work. The result of the calibration for $(V-K)\leq2.1$ is

$$\begin{eqnarray} \log (\Phi(K))=-4.5939829 -0.4560143 (V-K)\nonumber\\ -3.25133... ...} (V-K)^2 \\ \sigma=0.006\approx 1.5\%, 50\rm \;stars. \nonumber\end{eqnarray}$$ (4)

If we consider only stars with $(V-K)\geq2.0$, then

$$\begin{eqnarray} \log (\Phi(K))=-4.6538559 -0.4152091 (V-K)\nonumber\\ -1.62085... ... (V-K)^2 \\ \sigma=0.006\approx 1.5\%, 141 \;{\rm stars},\nonumber\end{eqnarray}$$ (5)

where $\Phi(K)$ is the so-called reduced flux to magnitude K, defined through the equation $F_{\rm Bol}=10^{-0.4\;K} \Phi(K)$. It should be noted that these calibrations are ultimately based on the optical absolute flux calibrations of Vega by Hayes & Latham (1975) and Tüg et al. (1977), and the IR absolute flux measured in Paper II.

 

Table 4: The same as in Table 1 for $\lambda_{\rm eff}=3690.0 ~ {\rm nm}$ (L' band)

  

Table 5: Bolometric correction to $K_{\rm TCS}$ magnitude versus $(V-K)_{\rm TCS}$

The corresponding bolometric correction for $K_{\rm TCS}$ magnitudes for giant stars obtained from Eqs. (4) and (5) is listed in Table 5, where the validity range of the calibration, in colour and metallicity, is shown. The differences from the bolometric correction obtained by applying the same method to main sequence stars are in the range 0.01-0.05 mag (Fig. 3).

In Fig. 4 we show the difference between bolometric corrections or fluxes derived here, and those from the following authors:

Bessell, Castelli and Plez (1998; BCP98)

 

This work comprehensively provides bolometric corrections synthesized from different grids of stellar model fluxes of solar metallicity. The comparison of the BC(K) scales in Fig. 4a shows a consistent agreement in the range (V-K)=1.4-3.6. However, in the borders of the colour range of our calibration differences increase. The discrepancies at the cooler edge of the temperature scale point are probably connected with the limitations of Kurucz's (1993) models under 4500-4000 K, however the reason for the discrepancy at the hotter edge is unclear.

Blackwell and Lynas-Gray 1998 (BL98)

 

This work presents a re-analysis of the results of Blackwell & Petford (1991) by using the same techniques. In Fig. 3c, we show the ratio of our bolometric flux to that of BL98 versus temperature for 50 giants common to both works. The mean difference is 1.4% (BL98 fluxes greater) with a dispersion of 1.7%. No appreciable trend with temperature is observed in the range 4000-8000 K. The offset is probably related to the different absolute flux calibrations adopted.

Flower (1996; F96)

 

This study provides a thorough analysis of the bolometric correction based on measurements of 335 stars compiled from the literature. For 37 giants common with our sample (mainly Population I stars), we have transformed the BC(V) provided in Table 3 of F96 to BC(K) adopting the following parameters for the Sun: BC$_{\odot}(V)=-0.12$ and $(V-K)_{\odot}=1.524$. From the comparison, two main features can be observed in Fig. 4b. The differences show a conspicuous slope with colour. The probable reason for this trend is coupled with the different temperature scales adopted in both studies. Furthermore the scatter about the mean line of differences is slightly larger ($\approx 3$%) than expected if one sums in quadrature the internal errors of both works. The explanation of this point, apart from the different temperature scales used implicity in the calculation, may be partly related to the inhomogeneity of the F96 sample and partly to the uncertainties introduced by the transformation from BC(V) to BC(K).

Bell & Gustaffson 1989 (BG89)

 

This study is based on a method similar to that applied here using instead 13-colour, UV and broad-band near-IR photometry. There are 21 common stars whose fluxes appear to be shifted 6% with a dispersion of 1.7% (Fig. 4c) from ours. This difference is probably connected with the absolute flux calibration and the photometric calibration of the 13-colour system. Notice that BG89 fluxes are also shifted 4-5% with respect to those of BL98, so that the relative differences with our work are consistent.

In summary, the agreement of the bolometric fluxes derived here for solar metallicity stars is within the error-bars expected from the sources of uncertainty affecting the various methods: errors in the absolute calibrations adopted in the optical and IR ranges, differences in the atmosphere models grids. It is worth noting at this point that a 3% error on the bolometric flux implies a 1% error in the temperature derived by mean of the IRFM.

  

Figure: a) Difference between the bolometric correction to $K_{\rm TCS}$ obtained here and those theoretically derived by Bessell et al. (1998): Solid circles: ATLAS9 Kurucz (1995) overshooting models, open circles: ATLAS9 Kurucz (1995) no overshooting models, solid triangles; NMARCS giant branch models of Plez et al. (1992), open triangles: NMARCS giant branch models of Plez (1995) b) Difference between the bolometric correction to $K_{\rm TCS}$ obtained here and that of Flower (1996); c) Ratios of the fluxes presented in this work to those obtained by Bell & Gustafsson (1989) (triangles), and Blackwell & Lynas-Gray (1998) (squares). Dotted lines show the internal error of our calibration (1.5%)

 

Table 6: Temperatures derived for the field stars of the sample. Column 1: Identification. The stars are ordered in right ascension. Column 2: Metallicity. Column 3: Surface gravity. Column 4: Bolometric flux in $10^{-2}~{\rm erg\;cm}^{-2}\;{\rm s}^{-1}$. Column 5: Interstellar reddening. Column 6: Temperature derived in band J (units are K). Column 7: Error in T_J computed considering errors in $F_{\rm Bol}$, monochromatic fluxes, log(g) and [Fe/H]. Columns 8-9: The same as in Cols. 6-7 for temperature derived in band H. Columns 10-11: The same as in Cols. 6-7 for temperature derived in band K. Columns 12-13: The same as in Cols. 6-7 for temperature derived in band L'. Column 14: The weighted mean temperature derived from T_J, T_H, T_K and T_L'. Column 15: Mean error computed by considering linear transmission of errors from Cols. 7, 9, 11 and 13. Column 16. Number of temperatures considered in the average of Col. 14

Table 6: continued

Table 6: continued

Table 6: continued

Table 6: continued

Table 6: continued

4.3 The reddening correction

A considerable number of the stars in the sample are distant from the solar neighbourhood ($D\gt 300\;{\rm pc}$), and consequently extinction corrections have to be applied. For this purpose, we have estimated E(B-V) for each star in the sample in order to correct both the bolometric and monochromatic fluxes. Where the values of the estimated extinction were considered significant, the colours have been corrected according to the extinction law ($A_{\lambda}=f(A_{V},\lambda)$) compiled by Landolt-Börnstein (1982). Two independent methods have been considered for assigning E(B-V) to field stars. The first one is based on the work by Anthony-Twarog & Twarog (1994), which provide E(b-y) obtained with the reddening maps of Burnstein & Heiles (1982). In this case, we have considered E(B-V)=1.37E(b-y) (Crawford 1975). The second one makes use of the extinction models for the galaxy compiled by Hakkila et al. (1997) and the distances calculated from Hipparcos parallaxes. The values obtained by Anthony-Twarog & Twarog (1994) are preferred for metal-poor giants, since the parallaxes of these stars are affected by errors which made the second method more uncertain.

As for the stars of globular clusters, we have adopted an average of the most reliable values quoted in literature, and, except for M 71, we have restricted our analysis to low reddening clusters.

In Tables 6 and 7 we present the reddening correction applied to the stars of the sample. It is worth noticing that a third of the field stars of the sample needed a reddening correction $E(B-V)\ge 0.02\;{\rm mag}$, and that $\sim$10% of them have $E(B-V)\ge 0.05\;{\rm mag}$.

The change in temperature induced by E(B-V)=0.05 mag when applying the IRFM varies from 2.1% at 3500 K to 4.5% at 7500 K. The hotter the star the stronger the effect since the proportion of flux radiated in the visible/UV wavelength range is greater.

4.4 Metallicity and surface gravity

The effective temperature determination by means of Eq. (3) requires an estimate of the stellar metallicity and surface gravity. These parameters, however, need not be very accurate as mentioned in Sect. 3.1. In particular, it may be concluded that 0.5 dex and 0.3 dex uncertainties in log(g) and [Fe/H], respectively, are sufficient to obtain temperatures to an accuracy of 1-2% (see Fig. 2). Therefore, as far as the surface gravity is concerned, it is enough to consider an average surface gravity according to the spectral type, although spectroscopic determinations of surface gravities have been adopted when available from literature.

A number of stars in the sample had their metal abundance determined from fine spectroscopic analysis included in the Catalogue of [Fe/H] determinations of Cayrel de Strobel et al. (1997) with a mean accuracy within 0.15 dex. We have preferred these determinations, but for stars lacking spectroscopic analysis, photometric metallicity calibrations based on Strömgren photometry (Anthony-Twarog & Twarog 1994), and on $\delta_{0.6}(U-B)$ index (Carney 1979), with accuracies oscillating between 0.20-030 dex, were used.

The adopted gravities and metallicities are listed in Tables 6 and 7.